电流谐波对永磁同步电机转矩谐波的影响研究

陈东锁，胡余生，陈 彬，肖 勇，张志东，史进飞

(1.广东省高速节能电机系统企业重点实验室，珠海 519070；2.珠海格力电器股份有限公司，珠海 519070；3.珠海凯邦电机制造有限公司，珠海 519070)

0 引 言

集中绕组内置式永磁同步电机在变频器供电时由于自身结构和变频器的原因，其电流激励中存在低次谐波和与变频器载波频率相关的高次谐波[1]。对于电流谐波与转矩谐波之间的关系，国内外学者分别从电磁功率[2-3]、磁动势[3-4]和气隙磁场[5-6]的角度完成了电磁转矩表达式的理论推导，但相关文献中未谈及高次电流谐波下的转矩谐波情况，存在局限性。

文献[7]研究了电流谐波次数对转矩的影响，但只停留在低次电流谐波对转矩平均值和转矩脉动的影响分析。文献[8]研究了电流谐波与转矩谐波之间的关系，还考虑到了实测电流谐波相序的存在，但只关注了低次电流谐波的影响。

另外，基波电流产生的转矩谐波次数和低次电流谐波产生的转矩谐波次数相同，两种转矩谐波分量相互影响[9]。而高次电流谐波产生的转矩谐波次数远大于基波电流产生的转矩谐波次数，两种转矩谐波分量互不影响。因此，从高次电流谐波方面研究有利于单独分析电流谐波对转矩谐波的影响规律。

本文在考虑电流谐波相序的情况下研究了电流谐波次数和转矩谐波次数之间的关系，其中重点关注了载波频率相关的高次电流谐波。

1 电机模型及电机实测电流

本文研究的集中绕组内置式永磁同步电机采用如图1所示的模型，其主要电机参数如表1所示，电机定子采用Y形连接。

表1 电机主要参数

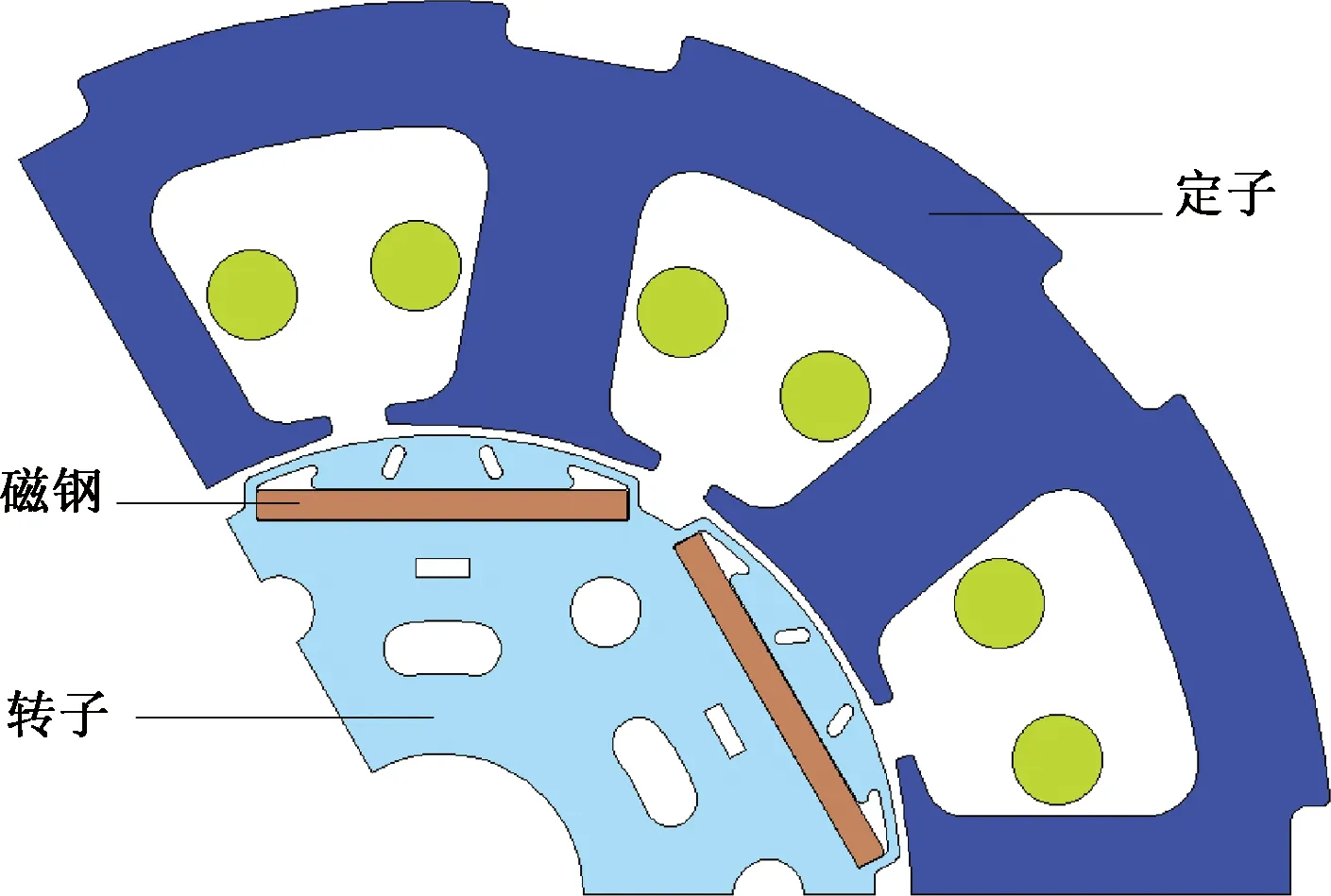
图1 电机模型

基于模型制造样机，并测得在变频器供电下的电机相电流，如图2所示。可知，变频器供电下电机实际电流并不是完全的正弦波，而是含有各次电流谐波分量。

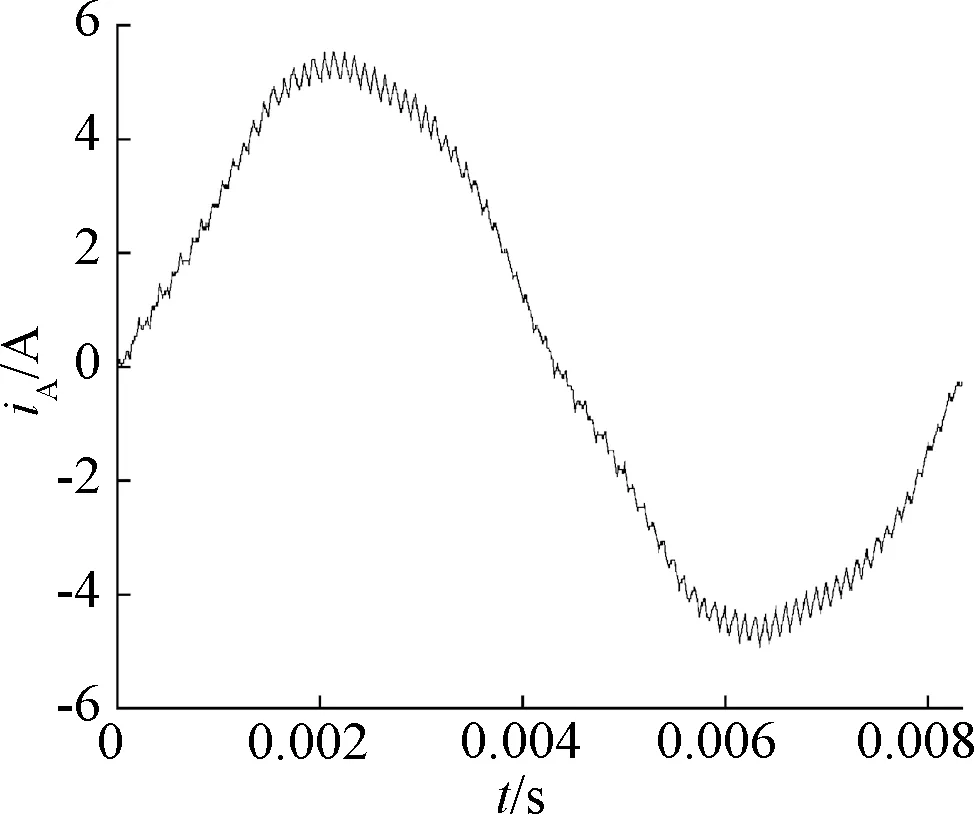
图2 电机额定转速时实测A相电流

对该相电流进行傅里叶分解，得到如图3所示的电流谐波分布情况。其中电流主要有5、7次等低次电流谐波和5 kHz载波频率倍数附近的高频电流谐波，其中1倍和2倍载波频率附近的高频电流谐波有：4 520 Hz(F-4f)、4 760 Hz(F-2f)、5 240 Hz(F+2f)、5 480 Hz(F+4f)以及9 880 Hz(2F-f)和10 120 Hz(2F+f)，其中载波频率F为5 kHz，运行电频率f为120 Hz。

图3 电机额定转速时A相电流谐波分布

2 电流谐波与转矩谐波次数关系

2.1 实测电流谐波下的转矩谐波次数分布

以实测三相电流作为激励源，对电机进行有限元仿真，得到相应的转矩仿真结果，对该转矩进行傅里叶分解，得到如图4所示的转矩谐波分布情况。

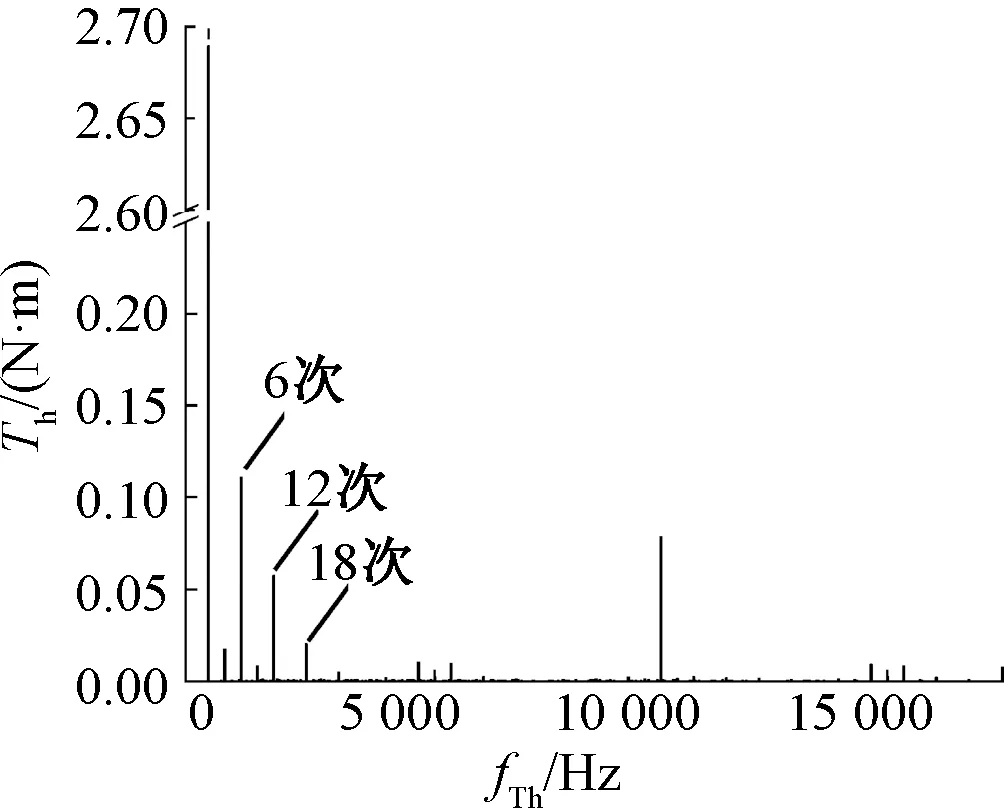
图4 实测电流下的电机仿真输出转矩谐波分布

从图4中可知，转矩主要有6、12、18次等6n次谐波和载波频率倍数附近的高频谐波，其中1倍和2倍载波频率附近幅值较大的高频转矩谐波有：4 640 Hz(F-3f)、5 360 Hz(F+3f)、10 000 Hz(2F)。

2.2 单次电流谐波下的转矩谐波次数研究

2.2.1 基波附加单次电流谐波表达式

上一节中，基于实测电流仿真得到了相应的转矩谐波次数分布情况，但实测电流中含有各次谐波。为了单独研究某次电流谐波与转矩谐波次数的关系，在考虑电流谐波相序的情况下设置了基波电流单独附加k次电流谐波的三相电流表达式：

(1)

式中:I1为电流基波幅值；p为极对数；f为机械频率；Ik为k次电流谐波幅值；λ为正负序系数，当电流谐波为正序时λ取1，负序时取-1；θk为k次电流谐波初始相位。

不同电流谐波的相序不同，且低次谐波相序与电流谐波次数相关。对于5、11等6n-1次(n为正整数)电流谐波，其B相电流相位超前A相120°，C相滞后A相120°，为负序电流；而对于7、13等6n+1次(n为正整数)电流谐波则相反，为正序电流。

对于高次电流谐波的相序，则依据实测三相电流谐波的相位差确定其相序。各电流谐波相序如表2所示。

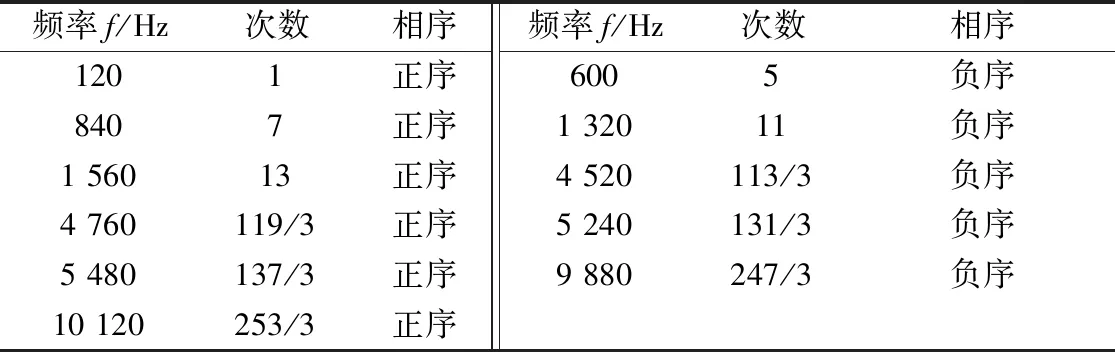
表2 额定转速下不同电流谐波的相序

2.2.2 单次电流谐波下的转矩谐波分布规律

为了定性地单独对比实测电流中不同电流谐波次数对转矩谐波的影响，设置式(1)中的电流谐波幅值为0.25 A，初始相位为0°，电流谐波幅值参考实测数据设置为4.9 A，作为电机的三相电流激励进行有限元仿真。

将基波单独附加单次电流谐波产生的转矩扣除基波产生的转矩即为该次电流谐波单独产生的转矩，并对其进行傅里叶分解，得到如图5所示的结果。图5展示了基波电流、各电流谐波单独产生的主要转矩谐波次数及相应的幅值，且各转矩谐波次数与图4中一致。

从图5中可知，基波电流下的转矩谐波分布在6、12、18等6n次谐波上，其中n为正整数；而对于5、7次等低次电流谐波，其产生的转矩谐波次数同样为6n次，未产生新的转矩谐波。

图5 基波、各电流谐波单独产生的转矩谐波分布

而对于113/3次等高次电流谐波，其产生了新的转矩谐波次数，且新的主要转矩谐波次数按照正/负序电流谐波，有如表3、表4所示的分布规律。

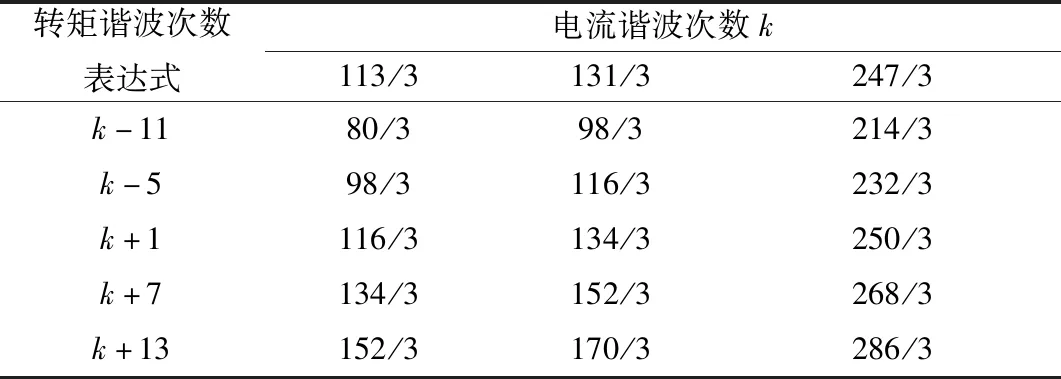
表3 负序高次电流谐波产生的主要转矩谐波次数

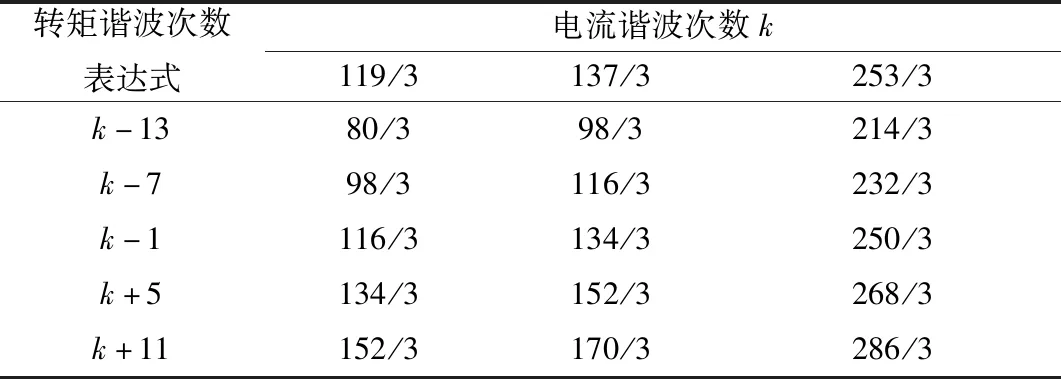
表4 正序高次电流谐波产生的主要转矩谐波次数

由表3和表4可知，相序相同的高次电流谐波产生的主要转矩谐波次数可用相同的转矩谐波次数表达式表示，并且该表达式与电流谐波次数k相关。例如，对于表3中负序113/3次电流谐波产生的80/3次转矩谐波，可用k-11=113/3-11=80/3来表示转矩谐波次数。并且正负序高次电流谐波的主要转矩谐波次数表达式相反。

进一步地，各高次电流谐波的主要转矩谐波的幅值按照表3、表4中的转矩谐波次数表达式，有如图6所示的分布情况。其中±号是将正、负序电流下主要转矩谐波次数表达式中的﹢、-整合一起表示。例如，对于k±1次转矩谐波，包括了113/3次等负序电流谐波的k+1次转矩谐波和119/3次等正序电流谐波的k-1次转矩谐波。

从图6中可知，各高次电流谐波的主要转矩谐波幅值基本一致，且按照幅值大小有：Tk±1>>Tk±11>Tk±5>Tk±7>Tk±13。

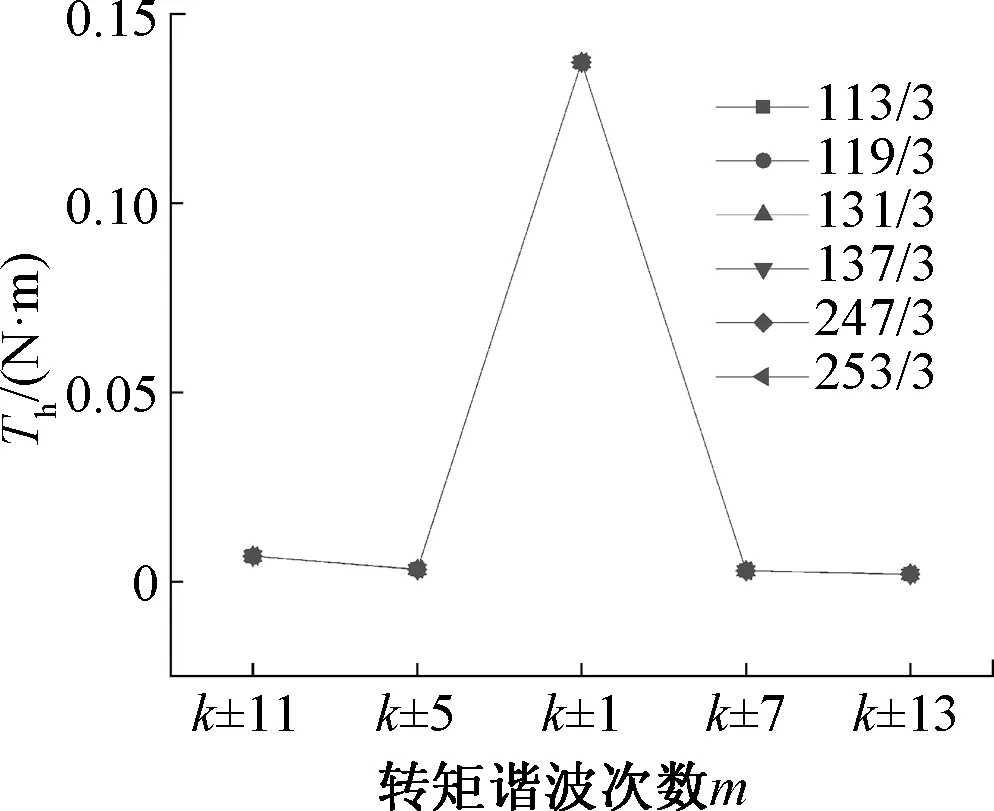
图6 各高次电流谐波下的主要转矩谐波次数及其幅值

2.2.3 原因分析

文献[5]已经介绍了正序和负序电流谐波下的转矩谐波次数分布，简单归纳如下：

(2)

式中：fTk为k次电流谐波下的转矩谐波次数；i为正整数；λ为正负序系数，当电流谐波为正序时λ取1，负序时取-1；其中|1-λk|次转矩谐波是由转子永磁体基波磁场和正/负电流谐波产生的空间p次电枢反应磁场作用产生的；|6i+1-λk|次(或|6i-1-λk|次)是由永磁体的(6i+1)p次(或(6i-1)p次)磁场和正/负序电流谐波产生的空间同次电枢反应磁场相互作用产生。

因此，当k次电流谐波次数为正序时，相应的转矩谐波次数为|1-k|，|6i+1-k|(|7-k|，|13-k|，…)和|6i-1+k|(5+k，11+k，…)；当k次电流谐波次数为负序时，相应的转矩谐波次数为|1+k|，|6i+1+k|(7+k，13+k，…)和|6i-1-k|(|5-k|，|11-k|，…)。

对于基波电流和7、13等6n+1次电流谐波，由于其相序为正序，故其转矩谐波次数为6i；对于5、11等6n-1次负序电流谐波，其转矩谐波次数同样为6i。

从表3和表4结果可知，对于高次正负序电流谐波同样满足上述电流谐波和转矩谐波的次数关系。

此外，因为转子永磁体中基波磁场最大，所以k次电流的空间p次磁场与转子基波磁场作用产生的|1-λk|次转矩谐波幅值最大，对应图6中的k±1次转矩谐波。

2.3 实验对比

电机样机和测试台如图7所示，电机仿真转矩和实验测试转矩如图8和图9所示。从图8、图9中可看出，实测结果与仿真结果整体趋势一致。

图7 电机样机及测试台

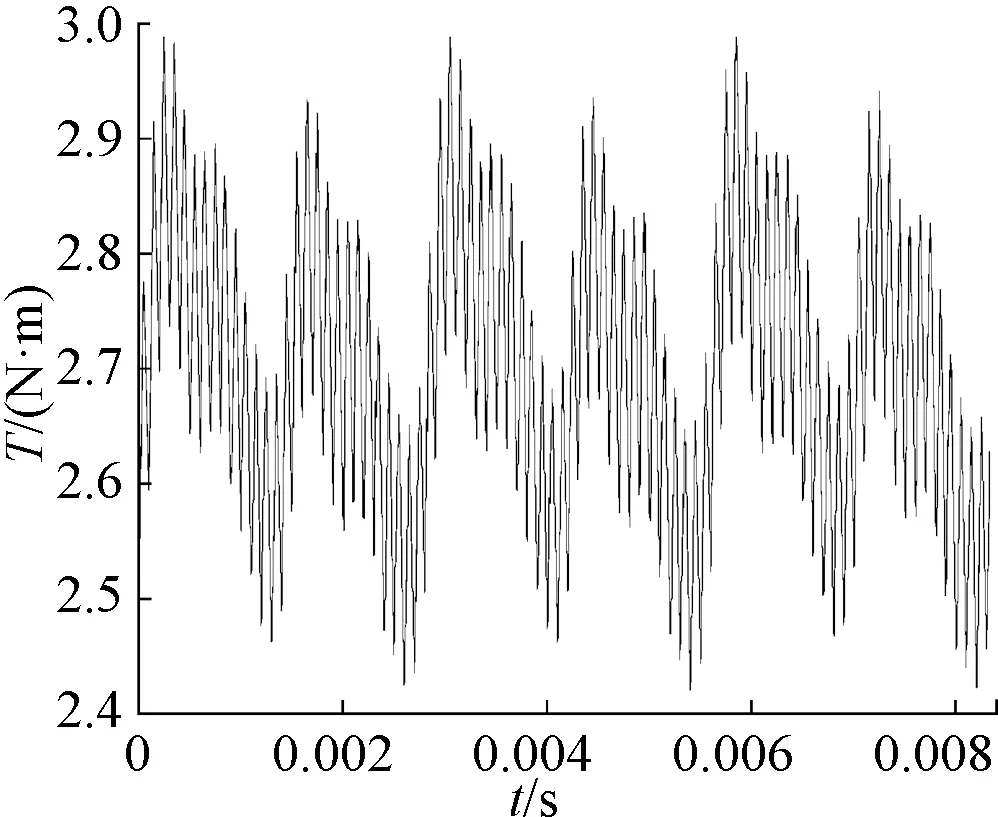
图8 电机有限元仿真结果

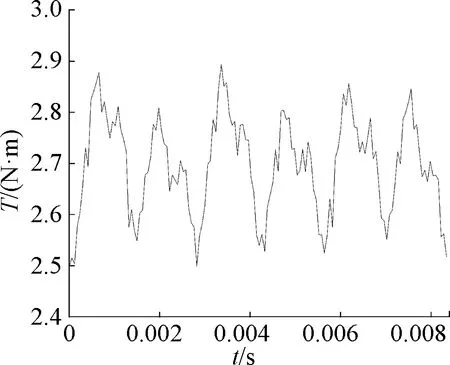
图9 电机实测结果

由于相关测试设备采样精度限制，高次转矩谐波特性无法体现，图10仅展示了实测和仿真转矩低频谐波的对比。从图10中可知，仿真和实测各低次谐波吻合情况较好。后续将重点关注高频转矩波动相关测试和验证对比。

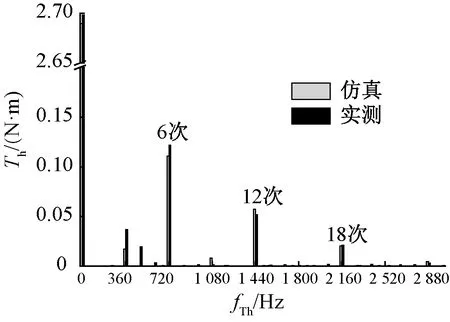
图10 电机有限元仿真和实测转矩低次谐波对比

3 结 语

转矩谐波是定转子谐波磁场相互作用产生的，转矩谐波次数与电流谐波的次数和其相序相关，其中对于k次电流产生的转矩谐波次数有以下规律：当k次电流谐波为正序时，其产生相应的转矩谐波次数为|1-k|、|6i+1-k|、|6i-1+k|；反之，为负序时，相应的转矩谐波次数为|1-k|、|6i+1+k|、|6i-1-k|。

上述电流谐波次数和转矩谐波次数规律适用于低次和高次电流谐波，后续可以根据已知的电流谐波特性(次数和相序)推论出相应的主要转矩谐波次数。