永磁直线同步电机多周期离散重复控制

王 欢，刘光欣

(1.天津大学 内燃机研究所，天津 300072；2.天津市瑞能电气有限公司，天津 300385)

0 引 言

永磁直线同步电动机(以下简称PMLSM)由于“零传动”的自身结构特性，具有低损耗、高精度、快响应等优点，在高速精密数控、精密仪器、半导体芯片制造等领域有很大的应用潜力。一方面，PMLSM固有的周期性推力波动[1]会影响伺服系统的性能，特别是在高精度、高响应速度的情况下尤为突出[2-3]；另一方面，当PMLSM伺服系统跟踪任意多周期(两个输入信号周期不成倍数关系)输入信号时，控制精度较差。为此，有的学者采用了人工神经网络控制[4]、变结构控制[5]、H∞滑模控制[6-7]等，但这些算法的高度复杂性会导致系统的调节响应滞后，并且由于周期信号的时变性，并不能较好地抑制或跟踪系统输入的多周期信号。因此，需要设计出一种相对计算简单又高效的控制算法来解决上述问题。

重复控制器在频域内首先由Inoue于1982年提出，控制器基于内模原理对系统外部周期性输入信号进行调节[7-8]。Tomizuka于1989年首次提出离散重复控制器，离散重复控制器具有如下优点：一是重复控制器数字实现比模拟实现要简便，二是由于离散化时限制了不必要考虑的高频分量，因此不切实际的输入条件不需要考虑，简化了求解控制器的过程。特别是Tomizuka提出的原型重复控制器，是以零相差跟踪为基础，采用零极点对消原理设计调节器，不需要求解复杂的Diophantine方程，缩短了计算机的执行周期，但是一般的原型重复控制器还有很多不足，例如对多周期输入信号的跟踪就显得束手无措[1,9]。

本文研究了一种快速调节(跟踪/抑制)任意多周期信号的新方法，并从实际出发提出了一种适用于PMLSM的多周期重复控制系统。首先将重复控制器的周期发生器的死区长度缩短为所有周期信号的输入之和。多周期重复控制器不仅可以比一般重复控制器少很多记忆单元来实现，而且可以使控制误差更快地收敛到零。其次，多周期离散重复控制系统不仅可以保证系统的稳定性，而且能将系统极点配置在以原点为圆心的给定半径圆盘上，增加稳定裕度。第三，所提出的控制器是显式，设计方法不需要求解Diophantine方程，即使输入信号的周期非常大，设计的工作量却非常小，这一点和一般离散重复控制器相似。最后，通过MATLAB/Simulink，解决了PMLSM控制系统多周期输入信号的跟踪/抑制问题，仿真验证了其有效性。

1 PMLSM传递函数

根据运动力学，对PMLSM的运动状态建立数学方程：

KFiq(t)-Ff-FL-Fripple

(1)

式中：M表示PMSLM的动子和其带动的负载总质量；x(t)为动子的位移量；Fe表示PMLSM的电磁推力；FL表示施加的外力，在系统中作为负载；KF表示电磁推力的系数；iq表示电机动子的q轴电流。

Fripple表示推力波动，是由端部效应产生的周期性波动函数。其与动子位移的函数关系[1]：

(2)

式中：Fripplem为端部效应产生力的波动幅值；τ为电机的极距；φ0表示电机初始相位的电角度[7]。

Ff表示摩擦力，数学表达式如下：

(3)

式中：fc表示库仑摩擦力系数；fs表示静摩擦力系数；v表示电机动子的运动速度；vs表示Stribeck影响速度；Bv表示粘滞摩擦系数。

建立状态方程，状态量分别为PMLSM的动子位移和动子移动速度，直线伺服系统状态方程表示：

(4)

式中:u=iq作为控制输入。

本文用d来表示将滞摩擦外的其他摩擦与干扰，即d=Ff+Fripple+FL。可以得到PMLSM的传递函数：

(5)

2 PMLSM伺服系统重复控制器设计

2.1 基于PMLSM的离散重复控制系统

图1是单输入单输出离散重复控制的PMLSM伺服系统框图。图1中，xd[k]，x[k]，e[k]，u[k]，d[k]，分别表示输入参考信号，输出位移信号，反馈控制误差，控制信号，干扰输入信号；C1(z-1)，C2(z-1)，P(z-1)则分别表示离散重复控制器，离散位置控制器和离散速度闭环传递函数，其中位置控制器使用的PD控制器，离散重复控制器是本文研究设计对象。

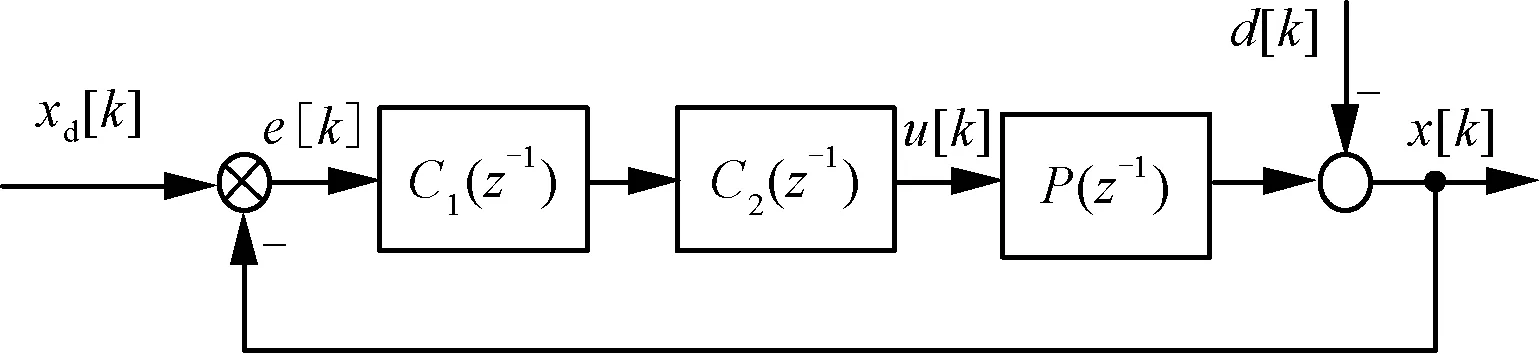
图1 离散重复控制的PMLSM伺服系统框图

假设图1的离散重复控制系统的采样间隔为Ts，d[k]的周期为L2，xd[k]的周期为L1，把xd[k]、d[k]分别离散化：

(6)

xd0(z-1)=xd0(0)+xd0(1)(z-1)+……+

(7)

(8)

d0(z-1)=d0(0)+d0(1)(z-1)+……+

(9)

式中：xd0(z-1)为xd(z-1)的第一个周期序列的z变换；z-1为延迟因子；d0(z-1)为d(z-1)的第一个周期序列的z变换[1]。

图1中的P(z-1)为PMLSM速度闭环离散传递函数，速度闭环控制系统框图如图2所示，P0(s)是被控对象传递函数。vd是速度环的输入信号，v是速度环的输出，d是干扰信号，速度控制器采用伪微分前馈反馈控制器(PDFF)结构，如图2虚线框内所示，控制器输出：

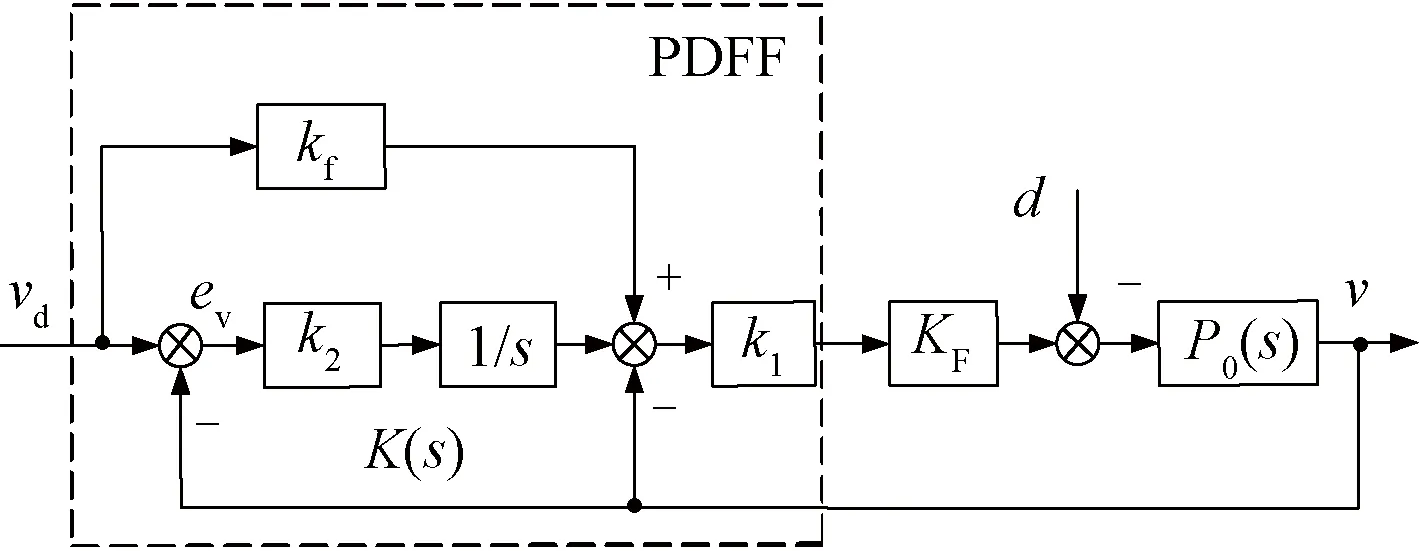
图2 PMLSM速度闭环控制系统框图

式中:k1表示主调节器参数；k2表示反馈补偿调节器参数；kf是PDFF调节器设计的关键参数，为调节器前馈比例增益。PDFF的引入加快了系统的响应速度，在误差没有经过积分环节时，让给定就提前加入了控制命令中。当kf=1，调节器为伪微分反馈控制(PDF)，当kf=0，为经典PI控制。PDFF调节器集成了两种控制器的优点，是介于两种控制方案之间的一种综合控制方案，既可以增加系统的抗扰动能力、增强DC刚度，又可以提高系统的响应速度，这两方面正是PI和PDF控制无法兼具的，本文采用的速度控制器为PDFF控制[7,11]。

对其求传递函数可得：

然后，对其离散化，可得P(z-1)。

2.2 离散原型重复控制系统

由于一般离散原型重复控制系统只能跟踪单周期信号，为了具有普遍意义，假设图1中的扰动信号d=0，PMLSM伺服系统可以用下式描述：

P(z-1)=z-dB(z-1)/A(z-1)

(10)

式中：B-(z-1)和A-(z-1)是互质的；z-d表示由被控对象造成的d步延迟，且

A(z-1)=1+a1z-1+a2z-2+…+anz-n

B(z-1)=b0+b1z-1+b2z-2+…+bmz-m

式中：b00，n≥m。

B(z-1)=B+(z-1)B-(z-1)，其中B+(z-1)包含所有渐进稳定的零点，B-(z-1)包含其它的零点，如不稳定零点。

根据图1可得系统闭环特征方程：

D(z-1)=S(z-1)A(z-1)(1-z-L1)+

z-dB(z-1)R(z-1)=0

(11)

式(11)即是Diophantine方程,选择合适的S(z-1)和R(z-1)使D(z-1)渐进稳定，即可完成重复控制器的设计，当L1数值非常大时，求解控制器的阶次会很高，尤其是在线求解方程时，复杂性变得不可容忍。取而代之提出下面的原型重复控制器：

(12)

式中：B-(z)是用z代替B-(z-1)中的z-1，由于B-(z-1)中包含不稳定的零点，所以不能直接对消，采用零相位对消法，即B-(z-1)B-(z)引入相位为零。h表示B-(z)的最高阶次，f是重复控制增益。最优重复控制增益fopt的求取方法如下：

(13)

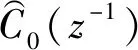
2.3 多周期离散重复控制器

当PMLSM控制系统需要跟踪多周期参考信号，或抑制任意周期干扰，即当d0时，上述一般离散重复控制器并不能实现零稳态误差跟踪参考信号，本文提出的多周期离散重复控制器既可以跟踪任意周期参考信号，还可以实现抑制周期性扰动，如固有的周期性推力波动等。

图1的控制框图同样也可以应用到多周期给定控制系统，xd[k]为多周期输入信号，设Li(i=1，…，l)，为了不失去一般讨论性，假设L1>L2>Ll是多周期参考输入信号的周期，d0的情况和多周期信号给定的推导过程相同，本文不赘述，以下推导过程都按照多周期给定信号进行。如果按照以往设计重复控制系统的经验，需要在控制器C(z-1)内部引入一个信号发生器1/(1-z-L),其中：

L=LCM{Li，i=1，…，l}

显然，这个L值会非常大，从控制器的计算角度和元素存储单元的大小来看都是不可取的。为了解决这一问题，简化控制器设计和减少存储单元，采用如下离散重复控制器的设计形式：

(14)

(15)

式中:h代表B-(z)表达式z的最高阶次，为了提高系统的鲁棒性,重复控制增益用Fk(z)零相位低通滤波器代替，是需要被设计的；hFk代表Fk(z)表达式z的最高阶次；α(z,Fi)=1-Fi(z)B-(z)B-(z-1),当l=2时，根据式(14)可得：

(16)

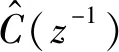
(17)

则当l=2时，多周期离散重复控制器表达式为下式:

(18)

控制框图如图3所示，零相位低通滤波器F1(z)、F2(z)可以根据下列公式设计：

(19)

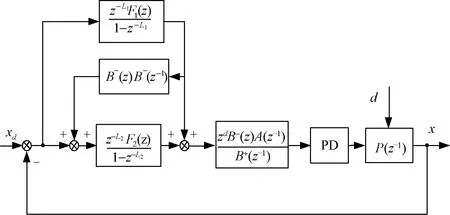
图3 基于多周期重复控制系统框图

2.4 多周期离散重复控制系统稳定性

稳定性定理：假设图3的离散重复系统是逐渐稳定的，且系统稳态误差为0，则存在零相位低通滤波器Fi(z)满足如下不等式：

(20)

且Li+d+hFi+h≥0，i=1，2，…，l，其中ωT∈[0,π]。

证明：多周期重复系统闭环极点特征方程：

(21)

(22)

由于系统是渐进稳定的，很明显存在z使z-Li=1，所以|Ge(z-1)|=0，则系统的误差也为0，可以看出，式(20)是设计低通滤波器的限制条件。

3 仿真结果及分析

为了验证本文理论的正确性，仿真采用的PMLSM具体参数以及位置、速度控制器参数如表1所示。直线电机标称模型为P0(s)=1/(12s+8)。

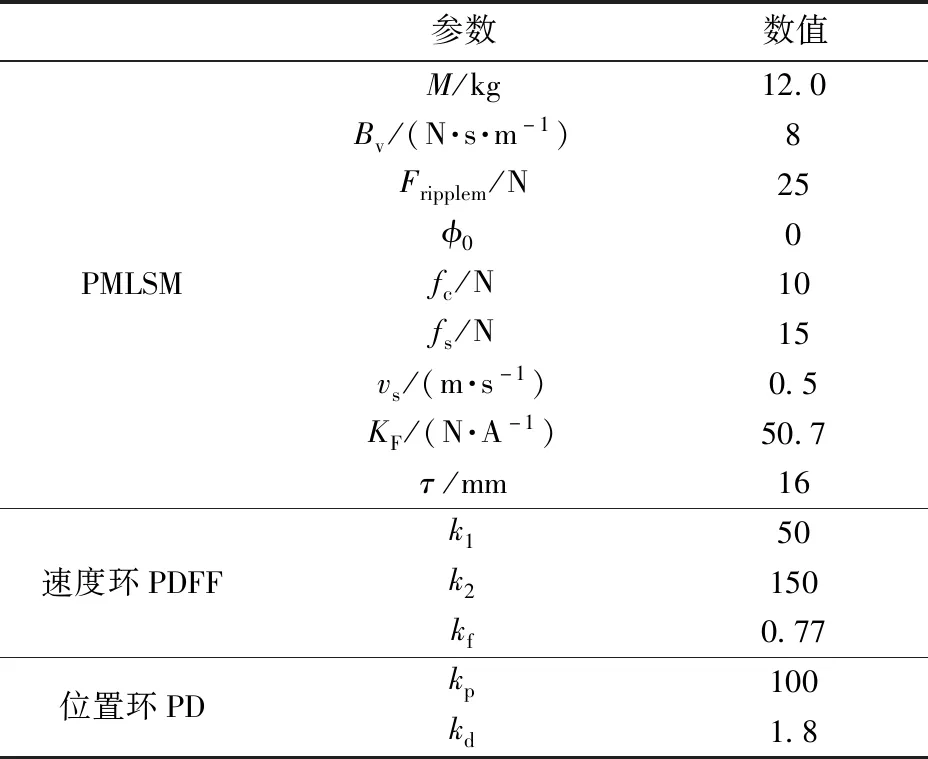
表1 仿真使用参数

系统的闭环传递函数:

F1(z)=F2(z)=fopt[1+1-B-(z)B-(z-1)]=

427.18-125.81z+125.81z-1

下面从两个方面仿真验证式(18)的控制器性能。

验证一：给定多周期信号，无扰动信号。

参考输入信号：xd10(t)=0.03sin(2πt)，xd20(t)=0.01sin(3πt)，xd(t)=0.03sin(2πt)+0.01sin(3πt)，如图4所示，两个输入信号不是谐波关系，采样间隔Ts=1/250 s。

图4 多周期信号给定波形

为了证明本文所设计的控制器的优越调节性能，采用上述离散原型重复控制器系统仿真做对比，控制器离散传函：

式中：L1=250，f=fopt，其余参数与多周期重复控制器参数相同。采用MATLAB/Simulink反复调试，得到如图5～图7的仿真结果，比较图5和图6，离散重复控制器跟踪多周期给定信号误差较大且不能收敛，而本文的控制器跟踪误差明显减小，几乎在0附近波动；从图7的位移输出波形也可以看出，多周期重复控制器无稳态误差跟踪多周期给定信号。

图5 离散原型重复控制系统给定与反馈误差波形

图6 多周期重复控制系统给定与反馈误差

图7 多周期离散重复控制系统输出位移

验证二：给定是单周期信号，有扰动。

xd(t)=0.03sin(2πt)，端部效应引起的周期性干扰信号：Fripple=25cos(125πt)，可得L={L1,L2}={250,4}，经过反复调试得到如图8～图11所示的结果。从图9和图10中可以明显看出，本文的控制器误差收敛能力和优越性。图11是本文设计的多周期离散重复控制系统的输出，可实现零误差跟踪输入。

图8 参考输入位移波形和推力波动波形

图9 离散原型重复控制系统给定与反馈误差波形

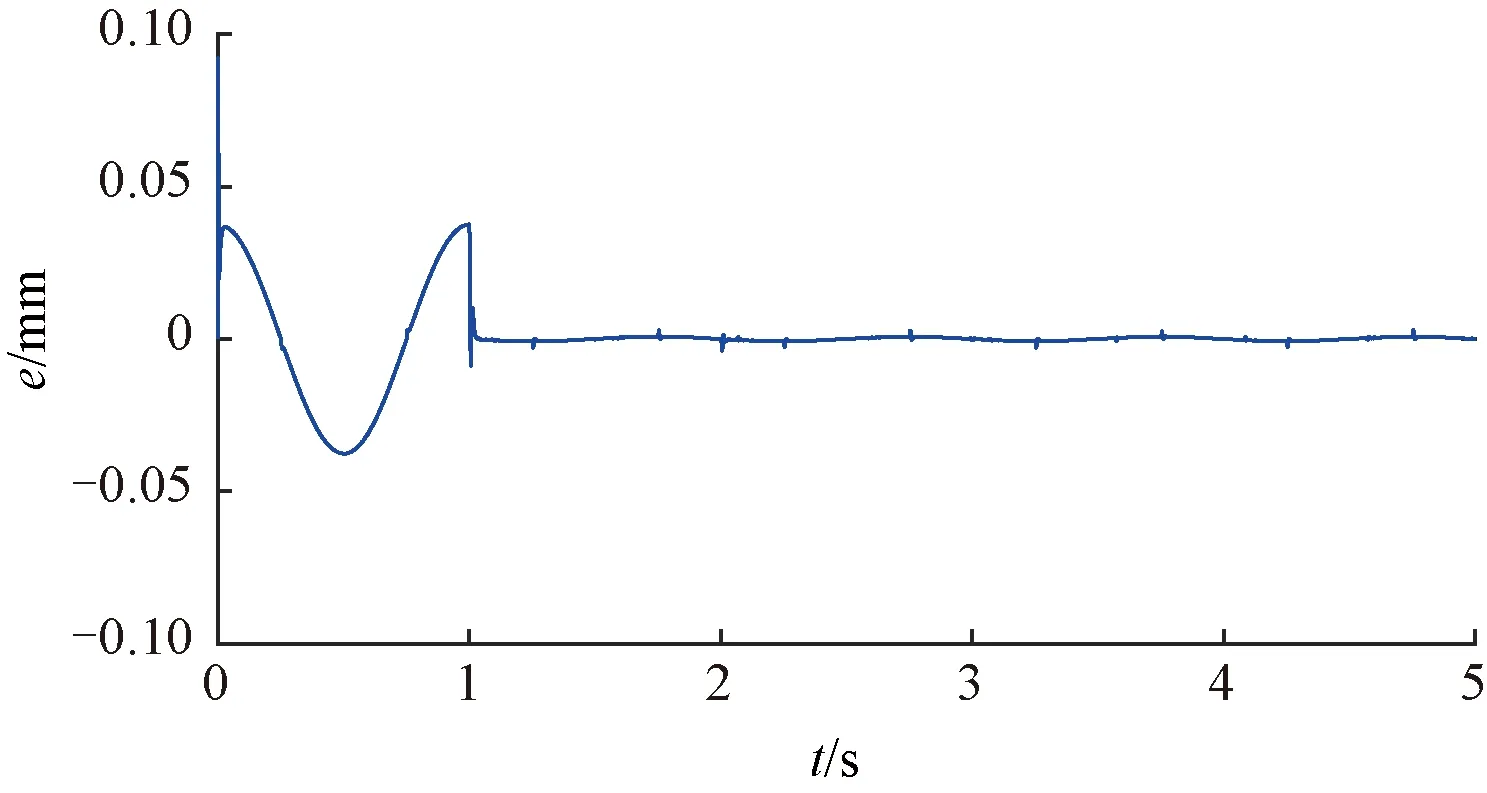
图10 多周期离散重复控制系统给定与反馈误差波形

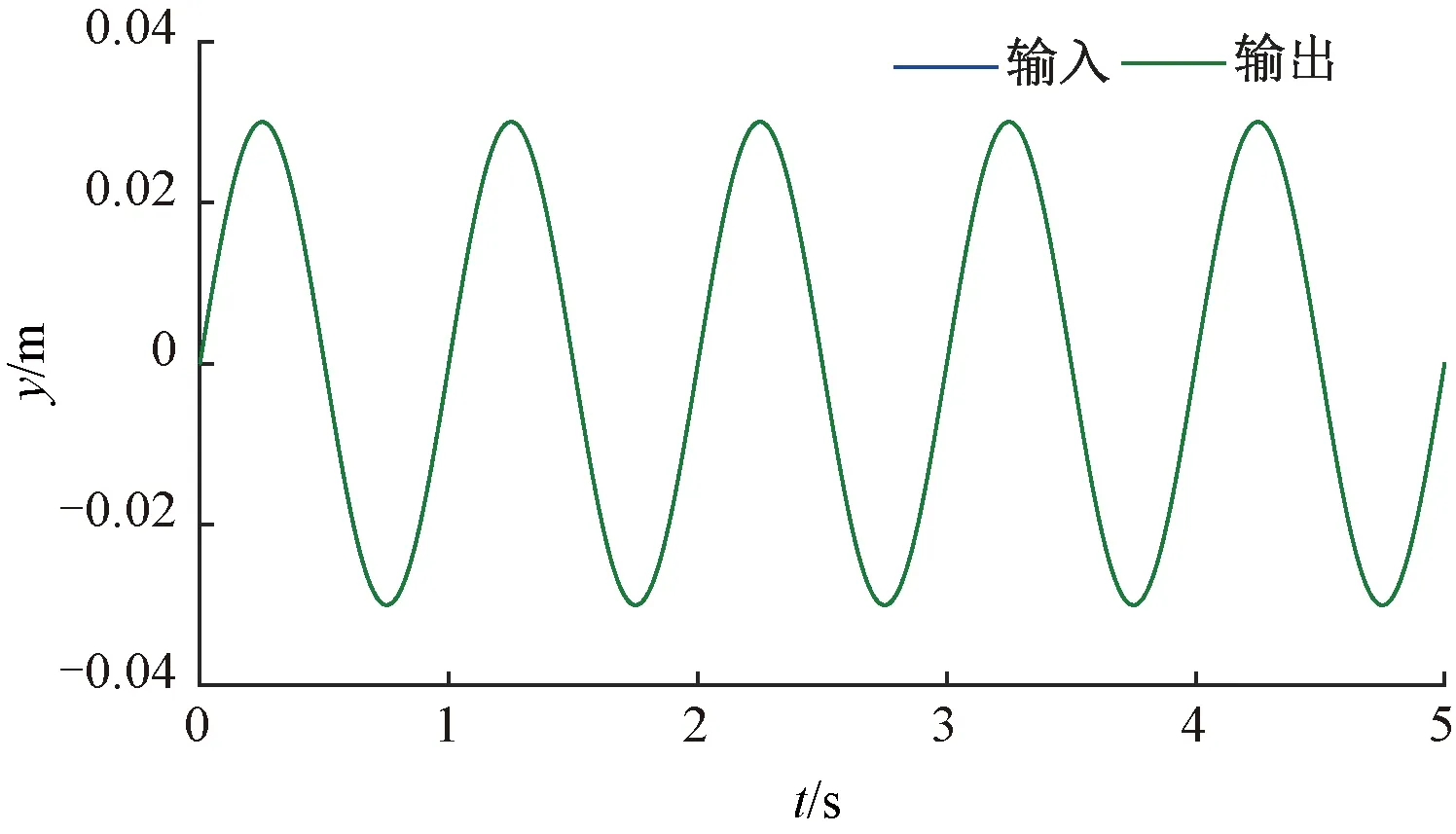
图11 多周期离散重复控制系统位移输出

图12为N1,N2不同取值时的系统误差收敛能力，其中N1,N2的取值如表2所示。可以看出，N的取值越大，误差幅值越小，系统的极点越接近原点。

图12 多周期离散重复控制系统不同极点设计系统误差

表2 低通滤波器参数设计和极点配置

4 结 语

PMLSM在跟踪任意周期输入信号时，伺服系统的位移跟踪精度下降，在任意周期性扰动存在的情况下也面临同样问题。为此，本文设计了一款新型控制器，使用两个改进原型重复控制器特殊的并联方式，加上通过设置控制器内部的零相位低通滤波器来改变整个系统的极点分布，在零误差跟踪/抑制多周期信号的同时，提高系统的响应速度。理论推导与仿真结果表明该方案的有效性。