基于长短期记忆网络的城市轨道交通系统通信延时补偿方法
黄子昊,李红波,张 超,徐东昇
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
基于大数据的智慧能源系统目前已成为业界关注的热点之一[1-3]。能量管理系统通过对海量数据的采集、整理和分析,提炼出能量管理策略,以提高能量管理水平,提升系统整体效益。为了进一步优化能源系统性能,实现能量实时管理,能源数据的实时性至关重要[4-6]。当能量管理系统包含较多分散布置的设备时,受物理距离影响,中心控制系统接收设备能源数据时普遍存在通信延时现象。延时会劣化中心控制系统的控制性能,其中闭环控制类功能对延时尤为敏感[7]。通信系统的性能在极大程度上决定了能源管理系统能够实现的控制功能。
城市轨道交通(简称“城轨”)作为高能耗产业,急需引入能量管理系统来优化系统能耗。城轨能量管理系统通过数据采集与监控(supervisory control and data acquisition, SCADA)系统来监控地面设备能源数据,主要涉及地铁主变电站、牵引站和降压变电所等场所[8-9]。列车通过车载网络通信系统实现不同车厢和设备间的数据互通和总集[10-11],之后再通过无线通信将数据传给地面[12-14]。目前车地无线通信被广泛应用于列车运行调度、隧道及弓网检测等领域。但无线信号传输易受外界干扰,与有线通信相比,延时和丢包现象尤为突出[15-16]。若在城轨能量管理系统中引入闭环控制,例如通过控制列车运行状态或能馈设备运行参数来改善能量流状态,那么车载数据的延时和丢包将会劣化能量管理算法效果,甚至会影响城轨能源系统的稳定运行。
列车功率曲线属于时间序列数据,在固定运行模式下存在一定规律,如牵引阶段速度较低时功率近似线性增加、惰行阶段功率平稳等,这是预测方法能用于通信延时补偿的基础。时间序列预测常采用统计回归模型,其差分原始序列数据后,再将序列表示为白噪声,与之前数据点移动、平均地组合;但差分操作丢失了数据绝对值,而列车功率绝对值隐含了当前列车运行模式这一重要信息,故统计回归模型不适合用于预测列车功率。神经网络可以逼近任意非线性函数,能够预测时间序列数据。列车瞬时功率与邻近时刻功率相关,因此本文提出一种基于长短期记忆网络(long-term and short-term memory network ,LSTM)的神经网络列车功率在线预测方法,其利用预测时间点前的功率数据来预测列车功率。
1 基于LSTM的神经网络
基于LSTM的神经网络[17]是一种改进型时间循环神经网络(recurrent neural network, RNN)算法,其拓扑是一条由数个相同神经元依次连接而成的链式网络。神经元基本结构中包含3个功能结构,即遗忘门、输入门和输出门,见图1。图中,Xt为t时刻神经元的时序数据输入;ht为t时刻神经元的时序数据输出;St为输出状态记忆单元,用于传递历史信息。
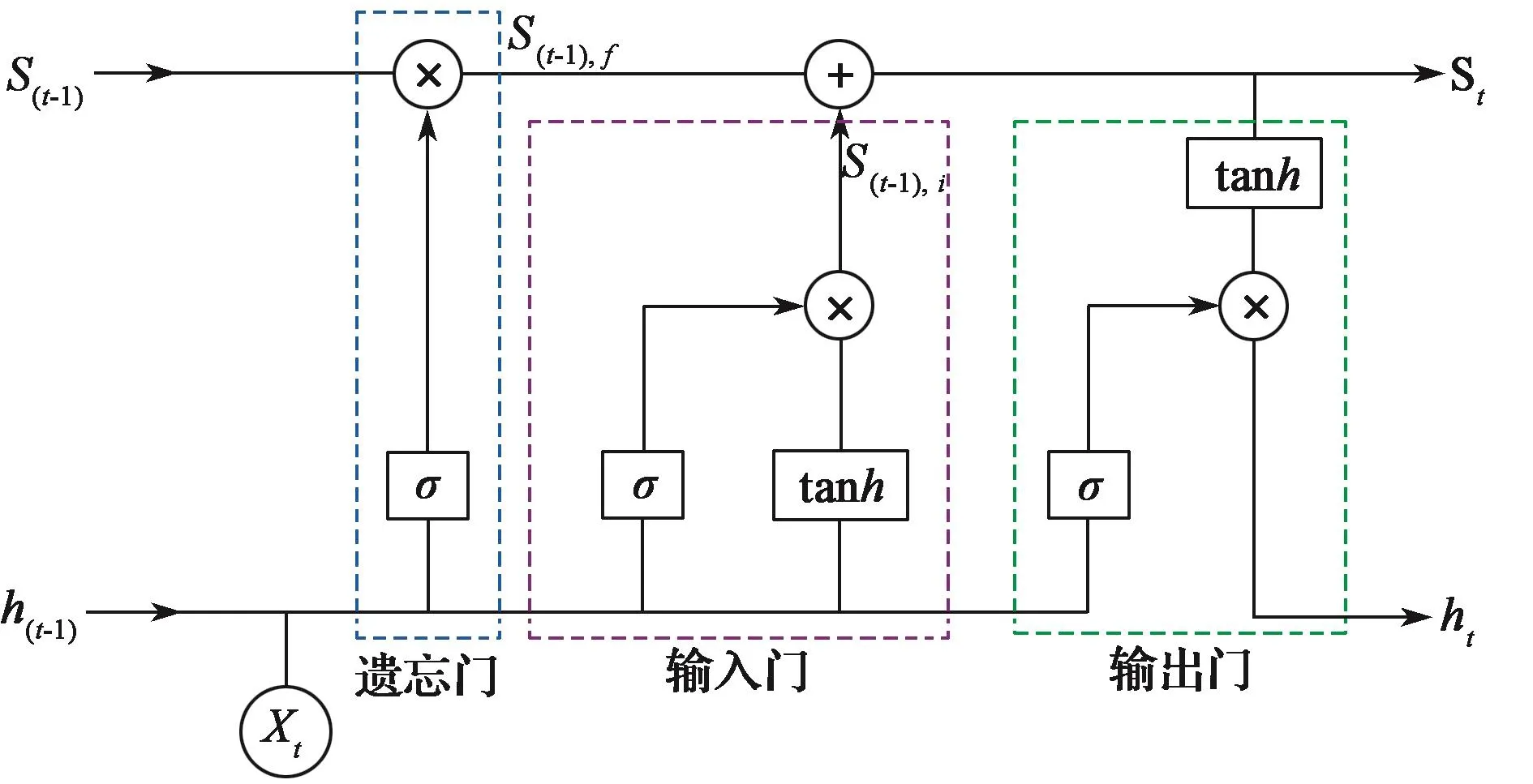
图1 LSTM神经单元拓扑图Fig. 1 Topology of LSTM neural unit
当神经元按时间顺序链式连接后,t时刻神经元输入包括(t-1)时刻神经元输出h(t-1)、输出状态记忆单元数据S(t-1)以及Xt。神经元遗忘门、输入门和输出门的输出分别如下:
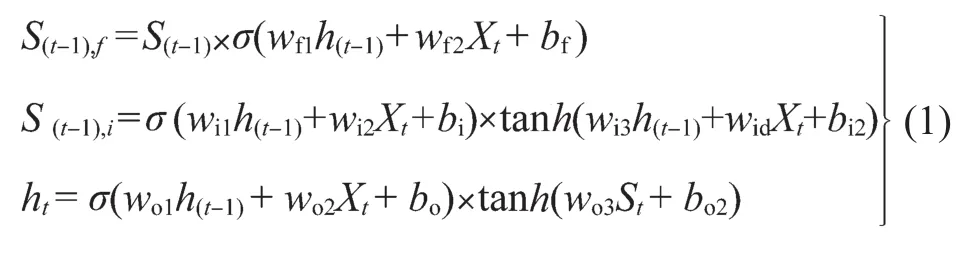
式中:σ——Sigmoid函数,其输出范围为[0,1];w——对应函数的权重;b——对应函数的偏置;下标中 ,t代表时刻,f代表遗忘门,o代表输出门。

Sigmoid函数用于控制信息的遗忘程度,其输出1表示信息全部流通,0表示信息全部遗忘,介于0和1之间表示信息部分遗忘。LSTM神经网络通过这种方式来实现信息的传递和遗忘。单个神经元中,遗忘门、输入门和输出门Sigmoid函数的参数分别控制这些门之间信息的遗忘程度。LSTM神经网络通过多个神经元的链式连接,实现时序信号间的信息记忆通路。图2示出3层LSTM神经网络拓扑,其中圆圈代表LSTM神经单元。t时刻将3个连续时序信号X(t-2),X(t-1)和Xt依次输送至链式连接的输入层,通过链式连接的隐藏层后,输出层输出(t+1)时刻的预测数据X(t+1)。
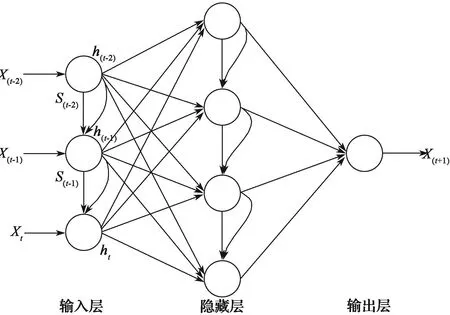
图2 LSTM神经网络拓扑Fig. 2 Topology of LSTM network
2 列车功率数据提取
本文的列车功率数据源于某市地铁现场试验。该试验共持续了3天,期间每天安排一位司机驾驶列车在线路上往返运行6趟,并利用4G无线通信模块进行车地通信。列车传动控制单元(driver control unit,DCU)模块通过4G通信模块每隔100 ms将当前列车实时功率数据发送给地面4G通信模块。图3示出连续3天司机每天在同一区间往返运行6趟的列车功率曲线(曲线间以开动时刻进行对齐)。为便于指代,将18次试验按时序进行编号,其中第一天司机a的试验编号为1~6,第二天司机b的试验编号为7~12,第三天司机c的试验编号为13~18。
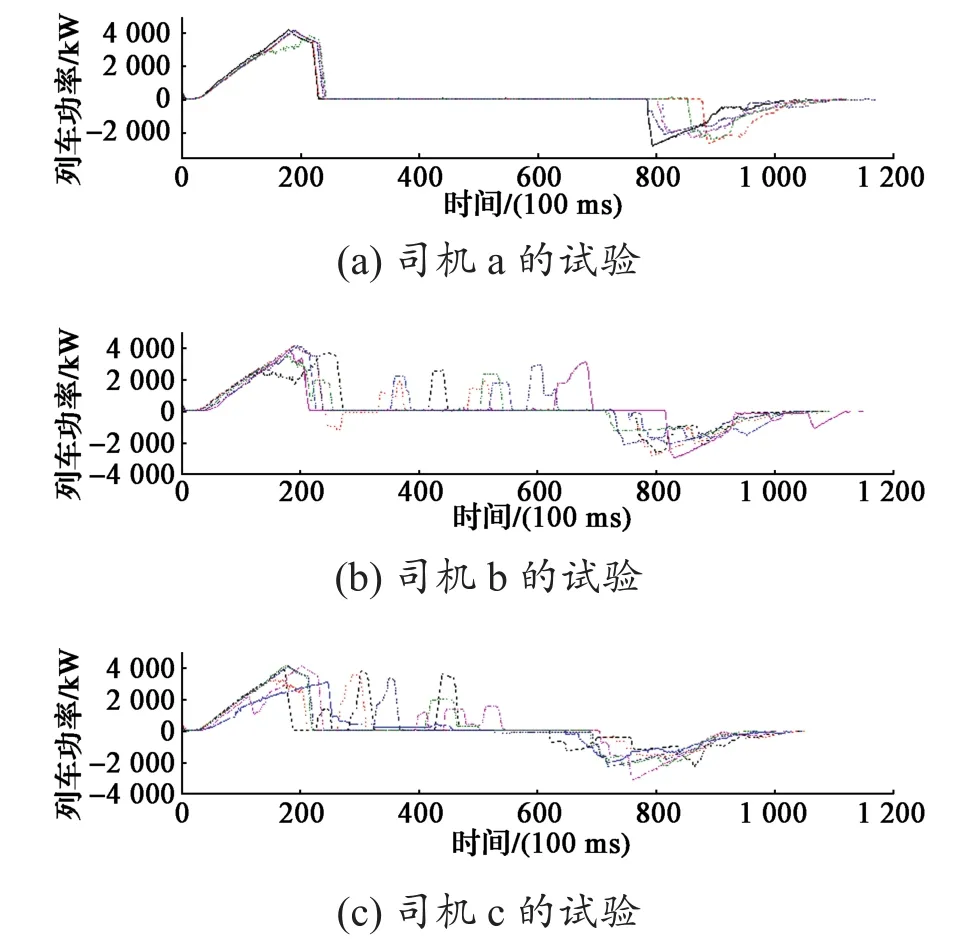
图3 列车3天的功率曲线Fig. 3 Train power curves in 3 days
列车功率曲线大致可分为牵引阶段、惰行阶段和制动阶段。以司机a的试验为例,其功率曲线具体如下:
(1)牵引阶段。司机在零时刻将司控器控制手柄推至全牵引位,列车进入牵引加速阶段,其功率近似线性增加;当列车运行速度逼近运行上限时,司机减小牵引运行级位,牵引功率下降。
(2)惰行阶段。列车运行速度达到上限,司机将司控器切换至惰行位。列车功率迅速降低到100 kW附近(具体功率范围主要由列车辅助用电决定,同时受地形上下坡影响),列车速度缓慢下降。
(3)制动阶段。列车即将到站,司机将司控器切换至制动位并调整制动级位,直至列车平稳进站、完成停车。
由图3可以看出,各司机的行驶习惯差异较大。如,司机a开行时间最长,司机c开行时间最短;司机b和司机c在惰行期间通过短时间改变列车运行级位来对列车速度进行调整。
同一司机重复开行的列车功率曲线特性也存在差异。要求各位司机尽可能保持驾驶习惯不变,在此前提下,在总运行时间不超过120 s的行驶过程中,同一司机在6次重复开行过程中制动起始时刻最大相差了10 s;司机b和c的牵引、制动特性在不同的重复开行趟次中存在较大差异,这是由于动态调整了列车运行级位所致。
纵观列车功率曲线,除了因司机切换列车运行级位状态而导致的功率变化,大部分时间列车功率大致保持平稳变化,而这是对列车实施功率实时预测的可行性基础。
3 基于LSTM的预测模型设计
本节基于图2的LSTM网络拓扑来设计列车功率预测模型,设计前先进行数据预处理和数据集设置。
3.1 数据预处理
为了消除不同数据间取值范围造成影响,先对所有列车功率数据进行归一化处理:

式中:Pnorm——归一化功率;P——功率原始数据;Pmin——功率最小值,本文Pmin=-3 200 kW;Pmax——功率最大值,本文Pmax= 4 200 kW。
3.2 数据集设置
数据集分为训练集、验证集和测试集。本文数据集包含了3位司机各重复6次共18组试验数据,每组试验数据包含1 000多个连续时序数据。其中,训练集采用第1, 2, 7, 8, 13组数据用于模型拟合训练;验证集采用第14组数据,用于评估训练模型的准确率,以避免模型过拟合;测试集采用剩余的12组数据,用于评价模型性能。
由于列车功率在不同运行阶段下的绝对值相差较大。为了定量分析预测数据和实际数据的偏差程度,本文采用代表归一化数据绝对误差的方均根误差(root mean square error, RMSE)δ作为评价指标。

3.3 模型设计
本文基于Keras深度学习框架来搭建LSTM模型,其后台为TensorFlow。LSTM模型参数包括输入层神经元数量、隐藏层神经元数量、激活函数、损失函数和优化函数。
3.3.1 输入层神经元数量
预测采用连续输入x个点预测第(x+1)点的滚动预测方法。为了确定输入层神经元个数x的取值,用训练集和验证集数据训练不同输入层神经元个数神经网络。不同输入层神经元的预测误差如图4所示。
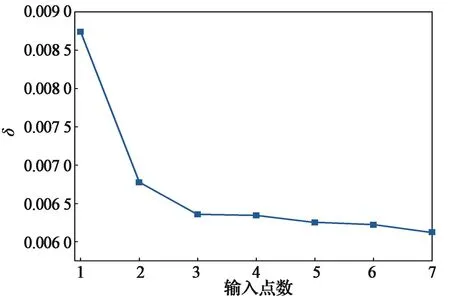
图4 预测模型输入点数和预测误差Fig. 4 Input number of predictive model and predictive error
预测误差随着输入点数增加而减小,但若输入点数过多,输入数据中遇到信号丢包的概率也会增大;且当输入点数大于3后,预测误差区别不大,基本可认为处于同一水平,说明瞬时功率与该时刻前两点数据关系最大。综合考虑,本文采用输入5点预测第6点的预测方式。
3.3.2 隐藏层神经元数量
隐藏层神经元数量若过少,则无法提供足够的拟合能力;若过多,则训练时间长,容易引起过拟合。为防止模型无法为不同输入层神经元个数提供足够的拟合能力,在通过验证集防止过拟合的前提下,本文选择隐藏层神经元数量为28,略大于经验公式的[18]。
3.3.3 激活函数
激活函数采用双曲正切函数tanh,其与Sigmoid函数曲线类似,但值域为(-1,1),且收敛速度比Sigmoid的更快[19]。
3.3.4 损失函数
损失函数采用均方误差函数(mean square error,MSE)。MSE为RMSE的平方,两者均可用于评估误差,仅存在量纲区别,3.2节采用RMSE是为了保持和列车功率的量纲一致。
3.3.5 优化函数
优化函数采用默认的Adam函数。
3.4 预测效果评估
预测效果评估包括3方面:通信参数指标、预测效果、掉包工况预测效果。
3.4.1 通信参数指标
预测算法用于补偿通信延时和解决丢包问题,只有明确通信延时和丢包指标后再评价预测效果,这样预测评估才有意义。为了模拟城市轨道交通跨城环境,通过Ping命令测试2个相距40 km的4G模块的通信情况。通信测试时,发送760个数据包,结果成功接收到747个数据包,丢失13个数据包,丢包率为1.71%。Ping命令最短耗时为147 ms,最长耗时为277 ms,平均耗时175 ms。由于Ping命令是双方应答式通信,因此,可认为单向数据传输平均耗时约87.5 ms。
车地实验时,车载DCU经传感器采样到数据包生成并发出、地面接收数据包并解析都需要额外的时间,且平均延时长于87.5 ms。为了便于分析,将列车数据传输延时与采样时间保持一致,设为100 ms,与本次列车试验数据采集间隔一致。列车连续发送n个数据点,当接收方接收第(n-1)个数据点时,列车此时真实数据为第n点,延时误差为相邻数据点的差值。
3.4.2 预测效果
预测模型输出的列车功率数据和实际数据分别如图5和图6所示。可以看出,当列车功率特性平稳时,预测误差总体较小。列车功率存在突变点时,预测误差增大。列车状态切换时,预测数据在功率拐点处存在1个点的滞后。
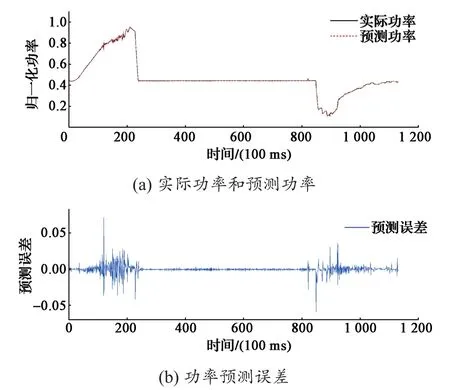
图5 实际功率和预测功率及预测误差Fig. 5 Actual and predictive power, predictive error
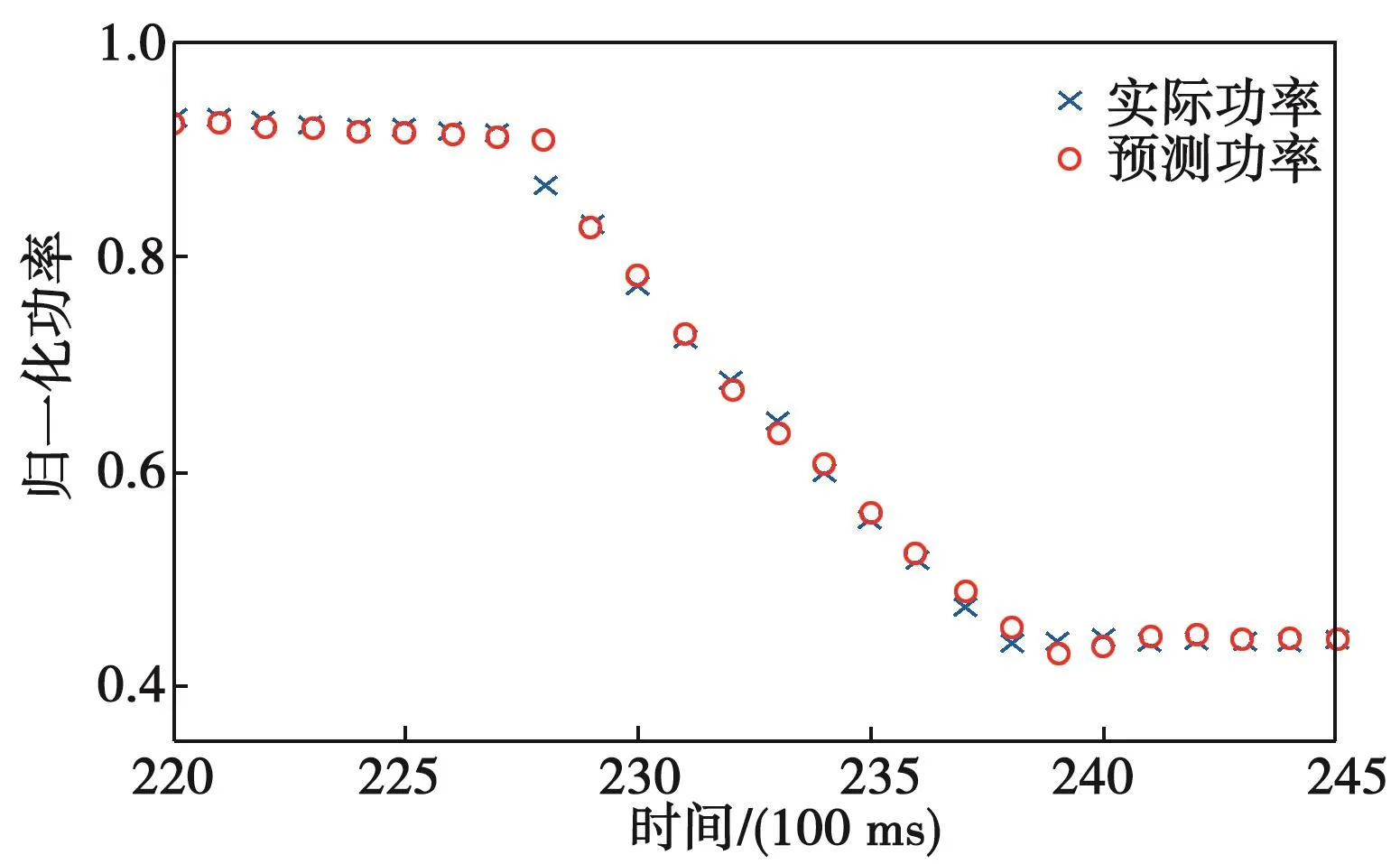
图6 实际功率和预测功率(局部)Fig. 6 Actual and predictive power (partial enlarged view)
为了对比通信延时误差和预测误差,分别计算各次试验的延时误差和预测误差RMSE(图7)。图7同时展示了司机驾驶行为对功率特性的影响。可以看出,司机a(试验序号1~6)的数据变化较为平缓,平均延时误差最小,预测优化效果较为稳定;司机b(试验序号7~12)的牵引加速曲线后半段差异较大,且惰行存在短时加速,平均延时误差高;司机c(试验序号13~18)的牵引加速曲线每次都存在较大差异,且牵引加速功率偏低,可通过后续惰行阶段的频繁加速来弥补。
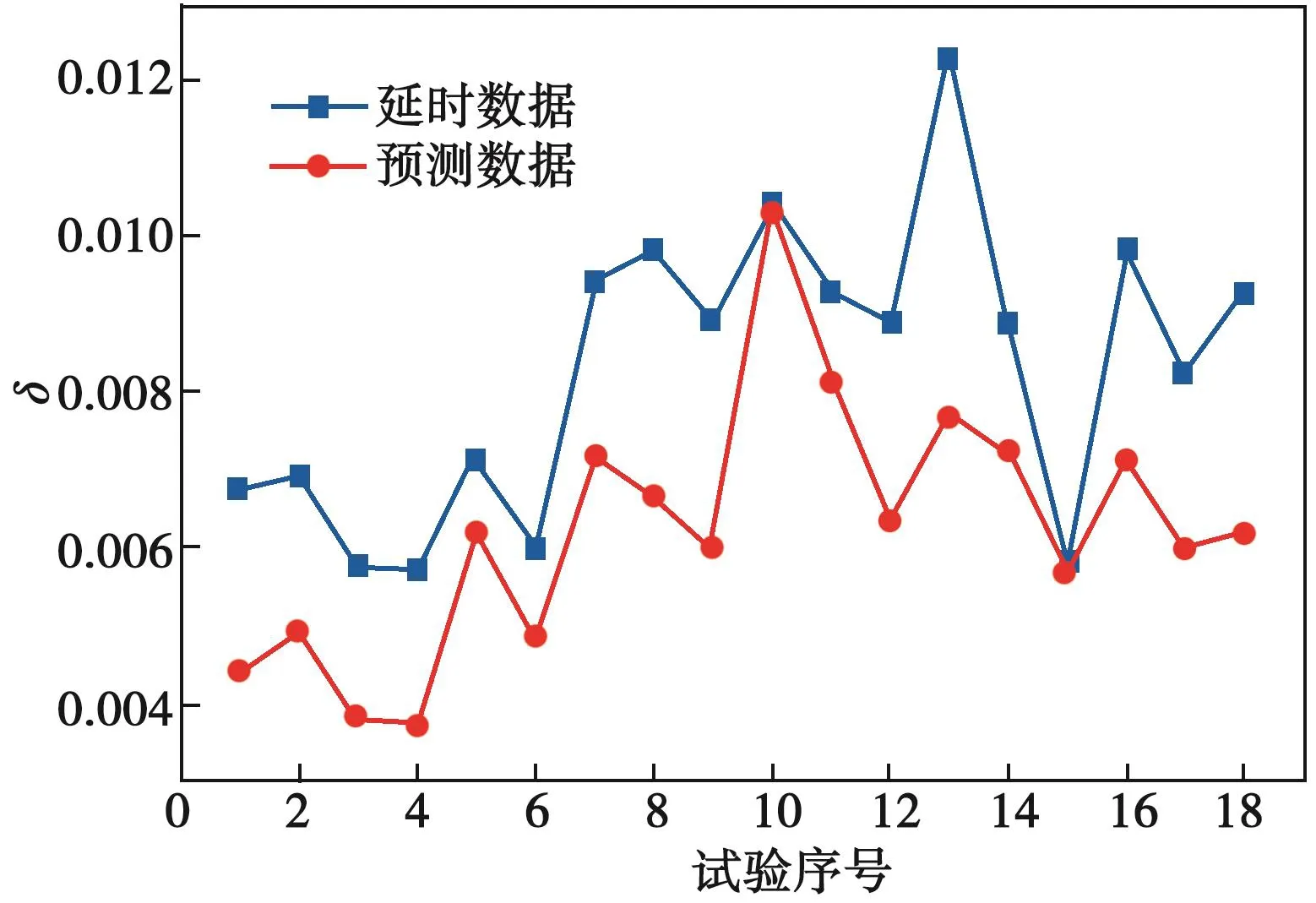
图7 延时数据和预测数据RMSEFig. 7 RMSE of delayed and predictive data
图7中,优化效果最差的为试验10和试验15,原始数据见图3(b)和图3(c)中实线。经查验,试验10惰行阶段50 s时刻附近存在多个超出正常惰行功率3倍的突变点;试验15在惰行阶段初期持续惰行20 s(超出正常惰行功率300 kW)和制动阶段都存在多次功率突变,劣化了预测效果。
由于训练数据参与了预测模型的训练,为公平起见,从结果中去除6组训练数据(试验序号1, 2, 7, 8,13, 14),得到的延时数据平均RMSE值为0.007 9,预测数据为0.006 2。换算为功率值,延时数据平均功率误差为58.73 kW,预测数据为45.88 kW。预测数据相对于延时数据误差改善了21.8%。
3.4.3 掉包工况预测效果
实际通信场景中,通信数据偶发掉包也是需要考虑的问题。假设n时刻应当接收数据包n,若没有收到,则视为掉包。从延时的角度考虑,当前最新数据仍为之前时刻接收的数据包(n-1),故掉包可以等效于增加一个数据包的延时。预测算法在掉包时,可将上一时刻的预测结果作为实际数据输入预测模型,对当前时刻数据进行滚动预测。
图8示出不同丢包点数下的预测数据和延时数据的RMSE。当丢包点数分别为0, 1和2时,等效通信延时分别为100 ms, 200 ms和300 ms;延时误差随着丢包点数的增加而急剧上升,分别为58.73 kW,103.60 kW和146.99 kW;预测数据分别45.88 kW,75.70 kW和109.03 kW,相对于延时误差减小了21.8%, 26.9%和25.8%。

图8 不同丢包点数下的预测数据和延时数据RMSEFig. 8 RMSE of predictive and delayed data with different dropout points
4 结语
为弥补通信导致的延时和丢包误差,本文设计了一种基于LSTM的列车功率在线滚动预测方法,其通过控制列车运行状态、能馈设备运行参数或其他能源设备状态参数,提高城轨列车能量管理系统数据的实时性,实时改善能量流,提升能源系统整体效率,从而提高能量管理水平。采用该方法后,延时功率误差可降低21.8%~26.9%。
受限于城轨列车的现场试验条件,本文未能实地测量列车在不同线路位置时(高架、隧道)通信参数的差异,线路和乘客对实际通信的影响也有待进一步研究。后续将研究自动驾驶策略下列车功率的预测算法,并增加其他相关信息(如线路条件、列车速度和工况),以提高预测精度。

