波纹度波数对深沟球轴承振动特性的影响
余光伟,方党生,蔡翔宇,周璐
(上海大学 机电工程与自动化学院,上海 200444)
球轴承结构简单,但其振动是一个复杂的问题。按激励源,球轴承振动可分为结构振动、内部激励以及外部扰动3类。结构振动主要由轴承自身结构引起,内部激励主要由轴承零件表面局部式缺陷、分布式缺陷等引起,外部扰动主要由轴承载荷、转速等工况条件引起[1-2]。国内外对球轴承振动激励的研究主要包括结构参数(球数、径向游隙、沟曲率半径系数等)、制造误差(波纹度、圆度、尺寸误差、表面缺陷等)和工况(载荷、转速、润滑条件等)3个方面。轴承制造商往往通过控制制造误差改善轴承动态特性,波纹度对轴承振动的影响尤为显著,是振动的主要激励因素。因此,以6201深沟球轴承为例,建立符合实际工程应用的轴承动力学模型和波纹度模型,分析波纹度对深沟球轴承动态特性的影响。
1 深沟球轴承动力学模型
1.1 接触特性
球与内、外圈沟道之间为点接触,基于线性回归的最小二乘法对赫兹接触理论进行简化,得到椭圆积分E,F,椭圆参数k的近似表达式为[3-5]
(1)
(2)
(3)
式中:∑ρi,∑ρe分别为内、外圈与球在接触点的曲率和。
主曲率有正负之分,凸面为正,凹面为负,曲率和可表示为
(4)
(5)
式中:Di,De分别为内、外圈沟底直径;Ri,Re分别为内、外圈沟道半径。
载荷与变形的关系为
Q=Knδ1.5,
(6)
式中:Kn为载荷-变形系数;δ为变形量;E′为等效弹性模量;E1,E2分别为球、套圈材料的弹性模量;ν1,ν2分别为球、套圈材料的泊松比。
由(1)—(6)式可得轴承内、外圈载荷-变形系数Ki和Ke,球与轴承内、外圈总的载荷-变形系数可表示为
(7)
1.2 动力学简化模型
假设轴承内圈固定,外圈旋转,测量球轴承振动值实际是测量轴承外圈振动,假设球均匀分布在内、外圈沟道之间且做纯滚动,不考虑球质量,将球视为弹簧和阻尼单元[6],球轴承可以简化为如图1所示的振动系统。基于牛顿第二定律,在轴向力Fa作用下,外圈三自由度振动微分方程为
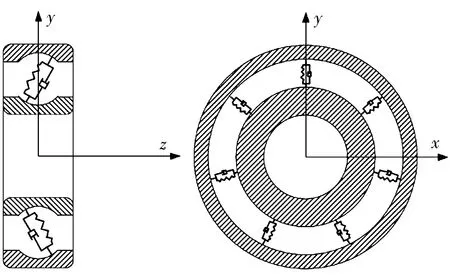
图1 球轴承的简化振动系统Fig.1 Simplified vibration system of ball bearing
(8)
式中:m为外圈质量;c为阻尼系数;x,y,z分别为外圈在坐标轴方向上的位移;Fx,Fy,Fz分别为作用在外圈上的弹簧力,即球与内、外圈的赫兹接触力之和。
作用在外圈上的弹簧力可表示为
(9)
hx=(Re-Ri)cosθj+x,
hy=(Re-Ri)cosθj+y,
hz=ze-zi+z,
ze=z0+Bdsinα,
zi=z0-Bdsinα,
式中:j代表第j个球;Z为球数;φ,ψ,χ分别为钢球位移向量与x,y,z轴方向的夹角;z0为球心相对坐标原点的初始位置;ωc为保持架角速度;t为时间;Bd为内外圈沟道中心距;α为初始接触角。
内外圈沟道中心距为
Bd=Ri+Re-Dw+Gr,
(10)
式中:Dw为球直径;Gr为径向游隙。
在外圈移动后,内外圈沟道中心距为
(11)
考虑内、外圈波纹度,第j个球的弹性变形量(外圈振动前后内外圈沟道中心距的差值)可表示为
(12)
式中:∏i,∏e分别为内、外圈波纹度值。
2 波纹度模型
影响轴承振动特性的因素很多,其中球波纹度、套圈波纹度是重要影响因素[7]。相对于沟道加工精度,球加工精度很高,G3级球的表面粗糙度Ra值已达0.01 μm。在此主要分析套圈波纹度对轴承振动特性的影响。
当套圈沟道表面不存在波纹度时,沟道表面为光滑曲面,球与沟道之间接触面的半径为恒定值。当沟道表面存在波纹度时,光滑曲面变为波纹曲面,球与沟道之间的接触变形和接触刚度发生变化,从而引起接触力变化[8]。
考虑球与内、外圈沟道之间存在间隙,轴承内、外圈波纹度可表示为[9]
(13)
Li(e)=ri(e)αi(e)mj,
λi(e)=πDi(e)/Ni(e)w,
式中:∏0为波纹度初始幅值;∏p为波纹度最大幅值;D为套圈直径;Nw为波纹度波数;αmj为第j个球与沟道的接触角。
对于外圈,
(14)
对于内圈,
(15)
式中:ωi为内圈角速度。
3 模型验证
以6201深沟球轴承为研究对象,其主要结构参数见表1,联立(1)—(15)式,采用四阶龙格-库塔算法求解三自由度振动微分方程。设定求解时间步长Δt=1×10-5s,转速为1 500 r/min,m=0.015 kg,Fa=70 N,Gr=4 μm,c=200 N·s·m-1[10]。

表1 6201深沟球轴承主要结构参数Tab.1 Main structural parameters of 6201 deep groove ball bearing
3.1 振动频率
通过上述模型仿真计算可得轴承外圈y方向的振动位移频谱图,由图2可知:外圈y方向位移频谱图在66 Hz处出现明显峰值,其他频率成分均为66 Hz的倍频成分。由于径向力的作用,在球轴承载荷区内,钢球奇偶交替变换,造成轴承外圈以外圈通过频率(BPFO)振动,即为球通过外圈沟道上一点的频率[8-9]。

图2 外圈在y方向的振动位移频谱图Fig.2 Spectrum of vibration displacement of outer ring in y direction
理论计算[5]可得,球通过外圈沟道上一点的频率为65.12 Hz,与仿真结果基本一致,验证了模型的正确性。
3.2 振动加速度
通过仿真计算可得外圈y方向上振动加速度(图3),振动加速度值均方根ai为0.16 m/s2,轴承振动加速度级可表示为
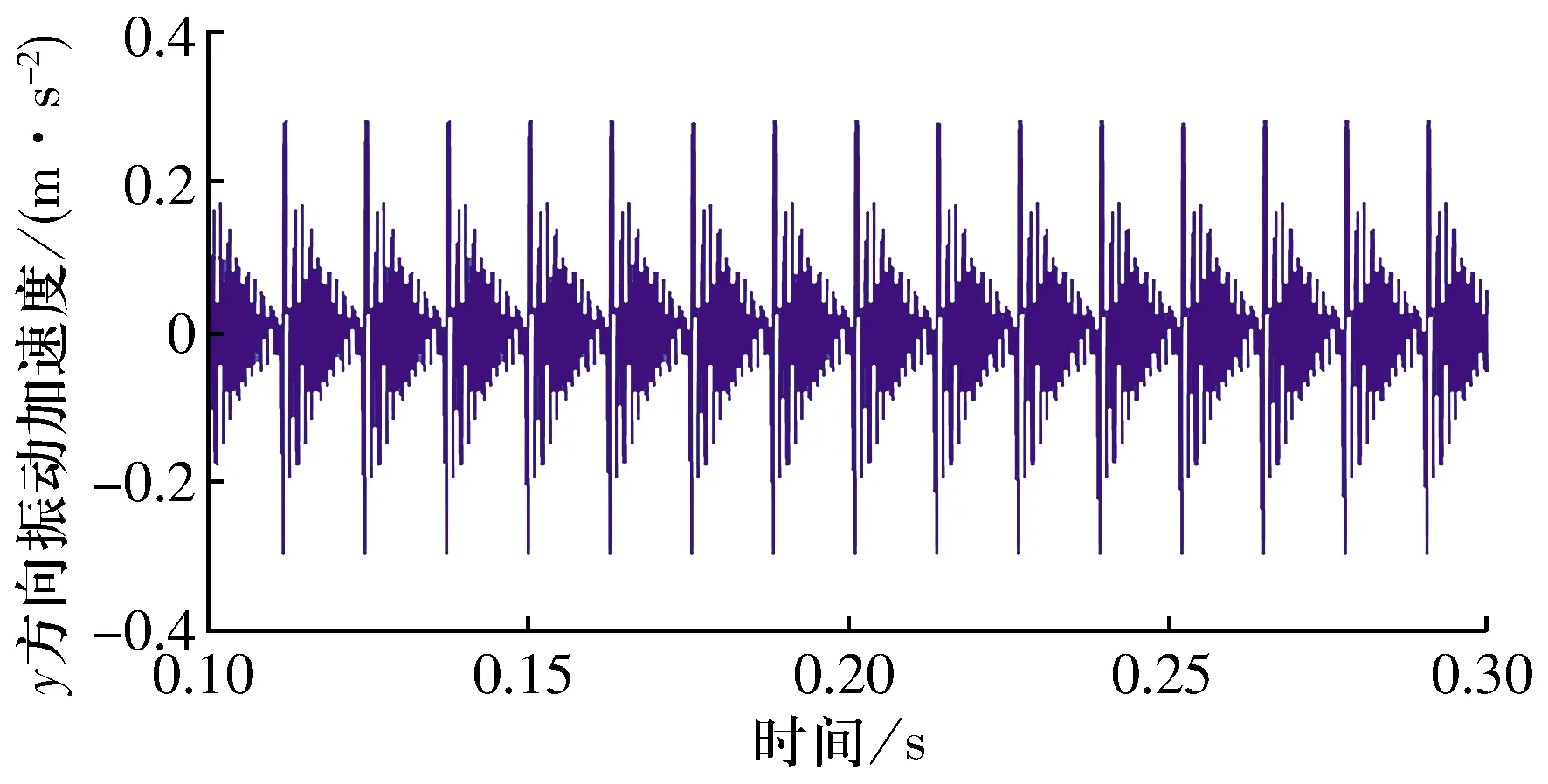
图3 外圈在y方向上的振动加速度Fig.3 Vibration acceleration of outer ring in y direction
(16)
式中:a0为振动标准参考值,一般取9.81×10-3m/s2。
通过(16)式可得轴承振动加速度级的仿真计算结果为24.19 dB。
取6套6201深沟球轴承,采用S092-3C轴承振动(加速度)测量仪测量轴承振动加速度,测量原理如图4所示。测量仪驱动转速为500~2 000 r/min,峰值测量范围为0~86 dB,有效值测量范围0~60 dB,采用16位数据采集卡。

图4 轴承振动加速度测量原理示意图Fig.4 Schematic diagram of measuring device for bearing vibration acceleration
参考GB/T 32333—2015《滚动轴承 振动(加速度)测量方法及技术条件》的规定,每套轴承正反两面各随机选取等距3个点测量[11],测得3点通频值取平均值,结果见表2。

表2 6201深沟球轴承振动加速度级测量结果Tab.2 Measurement results of vibration acceleration level of 6201 deep groove ball bearing
仿真结果与测量值误差为6.0%,误差在允许范围内,进一步说明了模型的正确性。
4 波纹度波数对深沟球轴承振动特性的影响分析
取轴承内圈波纹度初始幅值为0.01 μm,最大幅值为0.20 μm,外圈波纹度初始幅值为0.01 μm,最大幅值为0.30 μm,分析内外圈波纹度波数对轴承加速度峰峰值(最大值与最小值的差值)和有效值(RMS)的影响。
4.1 内圈
内圈波纹度波数为6,7,14,17,30,35,56,59时,轴承y方向的振动加速度随内圈波纹度波数的变化如图5所示,内圈波纹度波数为奇数时比偶数时的振动响应更明显。轴承y方向振动加速度的峰峰值和RMS随内圈波纹度波数的变化如图6所示,轴承y方向振动加速度的峰峰值和RMS随内圈波纹度波数增大而增大,且波纹度波数为球数整数倍时,变化曲线会出现局部峰值。
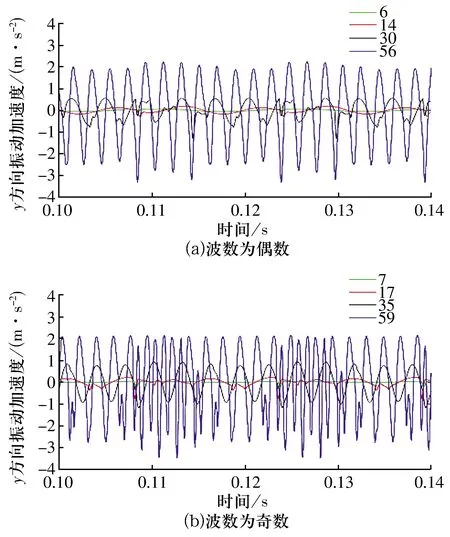
图5 轴承y方向振动加速度随内圈波纹度波数的变化曲线Fig.5 Variation curve of vibration acceleration of bearing in y direction with waviness wave number of inner ring

图6 轴承y方向振动加速度的峰峰值和RMS随内圈波纹度波数的变化曲线Fig.6 Variation curve of vibration acceleration peak-to-peak value and RMS of bearing in y direction with waviness wave number of inner ring
4.2 外圈
外圈波纹度波数为6,7,14,17,30,35,56,59时,轴承y方向振动加速度随外圈波纹度波数的变化如图7所示,外圈波纹度波数为奇数时比偶数时的振动响应更明显。
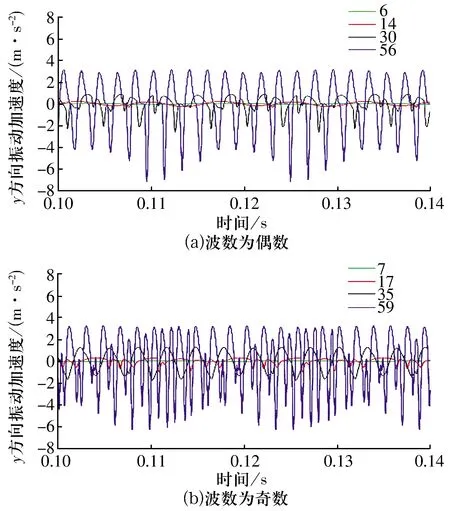
图7 轴承y方向振动加速度随外圈波纹度波数的变化曲线Fig.7 Variation curve of vibration acceleration of bearing in y direction with waviness wave number of outer ring
轴承y方向振动加速度响应的峰峰值和RMS随外圈波纹度波数的变化如图8所示,轴承y方向振动加速度的峰峰值和RMS随外圈波纹度波数增大而增大,且波纹度波数为球数整数倍时,变化曲线会出现局部峰值。对比图6可以看出,轴承y方向振动加速度的峰峰值和RMS随外圈波纹度波数变化略大于随内圈波纹度波数的变化。
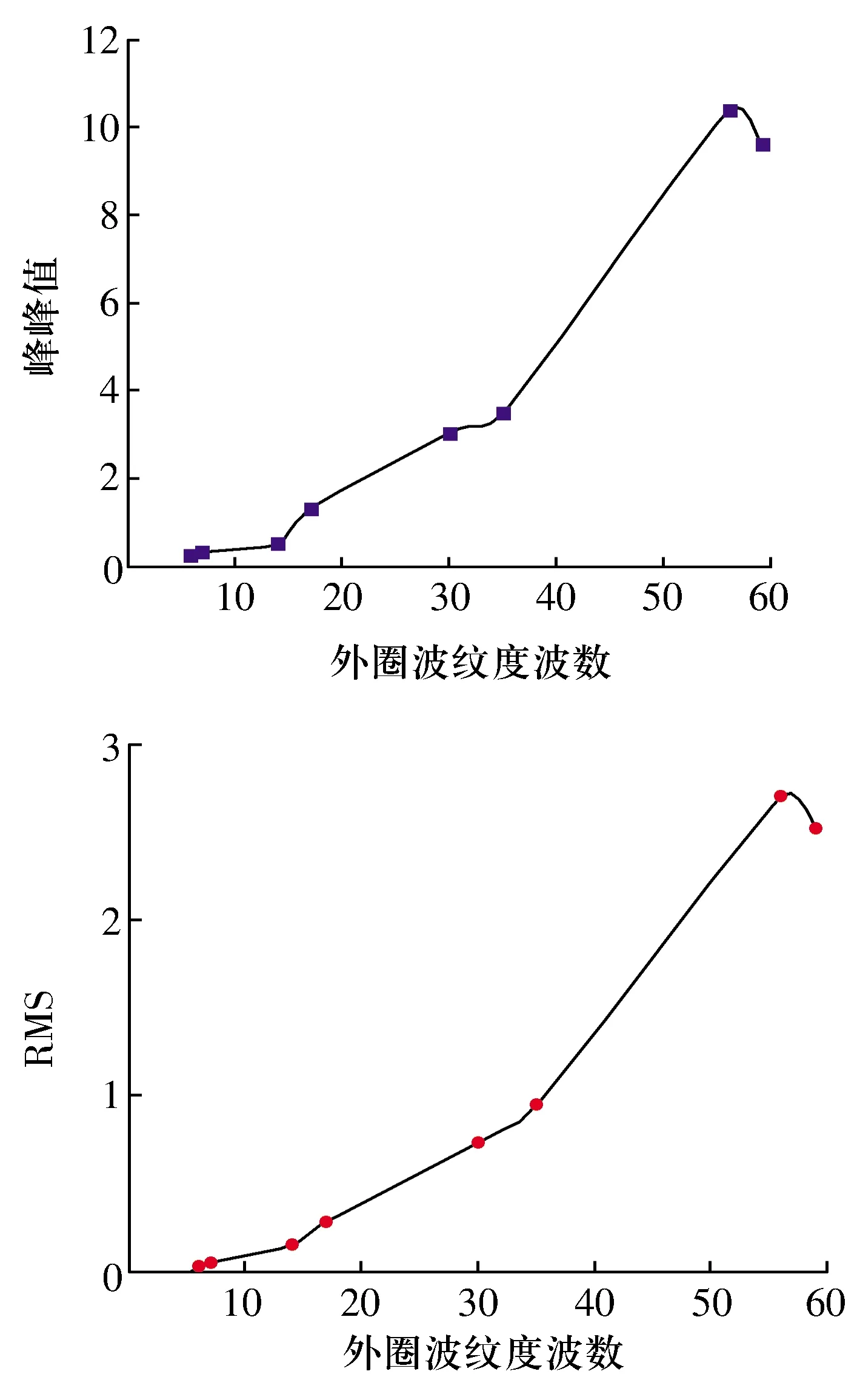
图8 轴承y方向振动加速度的峰峰值和RMS随外圈波纹度波数的变化曲线Fig.8 Variation curve of vibration acceleration peak-to-peak value and RMS of bearing in y direction with waviness wave number of outer ring
5 结论
建立了三自由度轴承动力学模型和波纹度模型,以6201深沟球轴承为研究对象,验证了模型的正确性,并分析了内、外圈波纹度波数对深沟球轴承振动特性的影响,得出结论:
1)内、外圈波纹度波数为奇数时均比偶数时轴承的振动响应更明显。
2)轴承振动加速度的峰峰值和RMS随内外圈波纹度波数增大而增大,波纹度波数为球数整数倍时,峰峰值和RMS随波纹度波数的变化曲线会出现局部峰值。
3)轴承y方向振动加速度的峰峰值和RMS随外圈波纹度波数变化略大于随内圈波纹度波数的变化。

