“和”“或”替代的子集原则与标记理论
李天一,彭家法
(安徽大学 文学院,安徽 合肥 230039)
汉语“和”表示联合或并列关系,“或”表示选择关系,和、或的使用条件是十分清楚的[1-3]。然而实际语料中,“无论/不管/不论”条件句[4-5]肯定否定并举做主语以及否定结构[6-8]中的“和”都可以换成“或”。
现有研究虽然指出了汉语和、或替代出现的结构,但相关的研究仍是零散的、不全面的。因此在现有文献的基础上,需要进一步关注和、或替代的结构有哪些,在可以替代的结构中二者的使用频率是否一样,有没有某种倾向性,这就需要对“和”“或”的性质和特点进行详细考察。
一、汉语“和”“或”替代使用的结构
以下将从否定结构和量化所有结构两方面来探讨汉语和、或相互替代的情况。
(一)否定结构中和、或的替代
吴静、石毓智、郑连忠、李占炳从语义逻辑的角度将否定词与逻辑学中的“否定”联系起来,将并列连词与“合取”“析取”联系起来。[6-8]虽然自然语言中的否定词与并列连词并不完全等值于逻辑学中的真值函项连接词[9],但是借助于这些形式符号可以帮助我们更直观地理解结构中各个成分间的语义关系。
(1)准确地使用会计科目,不得简化或用代号。
(2)不得加以检查和扣留。
例(1)虽然用的是“或”,但并不表示选择关系,而是表示联合关系,即对会计科目的使用,既不得简化,也不得用代号。我们可以借助德·摩根定律(De Morgan’s Law)来解释这一语义表达,根据德·摩根定律“否定析取”(p∨q)≡p∧q,此时的“或”作子集解读②。例(2)中的“和”可以换为“或”,但这与德·摩根定律“否定合取”(p∧q)≡p∨q无关,因为按照“否定合取”来解释,对应的语义表达是不得加以检查或者不得加以扣留,这明显与例(2)表达的意思不一致。例(2)的解读跟否定词和并列连词的语义辖域有关,它的语义辖域为“不得”取窄域,“和”取宽域,语义表达为不得加以检查并且不得加以扣留(p∧q)。如果将例(2)中的“和”换成“或”,此时的“或”作子集解读,即p∧q,替换前后语义辖域一致,二者自然可以相互替换。
简单来说,否定结构中的“和”不能按照表层的辖域关系去对应“否定合取”(p∧q),而应从深层的语义辖域出发p∧q。只有当“或”作子集解读p∧q时,否定结构中和、或的语义辖域一致,二者才可以相互替代。
(二)量化所有结构中和、或的替代
量化所有结构指包含全称量化词或表示所有义的结构,具体包括无论条件句、肯定否定并举做主语的结构、“即使/如果”假设句、全称量词句。首先看吕叔湘、吴静、石毓智所说的无论条件句、肯定否定并举结构中“和”“或”替代的情况:
(3)无论花朝与月夕,俊侣或良朋,赏心兼乐事,不回头便罢,一回头,这灰色的影子必定立刻扭扭搭搭地走了过来。
(4)接纳和不接纳都会引发尖锐冲突。
这两例不同于否定结构,它们无法用德·摩根定律来解释,只能从语义或子集解读上来解释。例(3)中“与”“或”“兼”的共现清楚表明了这里的“或”做子集解读。“无论……(都)……”是无条件关联词,即不管偏句的内容是什么,正句所表示的结果是一样的。[3]这一构式的意义使得和、或之间的区别消失了,例(4)也是如此。其他的例子如:
(5)智能卡安全可靠,即使失落或被盗,别人也无法使用。
(6)如果在不能吸烟的地方吸烟或乱丢烟头,都要罚几百新元。
(7)任何流行病或寄生虫病都可能造成毁灭性灾难。
前两例我们称为即使假设句。例(5)虽然没有明显的全称量化词,但可以用“即使……也……”这一构式来表示全称量化义。例(6)表示吸烟和乱丢烟头都是不可以的,这里的“或”作子集解读。全称量词句(7)的全称量化词取消了和、或的差异。
概而言之,和、或替代的结构可以分为两大类:否定结构和量化所有结构。量化所有结构或者有显性的全称量化词,或者有隐性的表示量化所有义的构式或词语。不管是否定结构还是量化所有结构,和、或的替代都要受子集原则的影响。
既然否定结构和量化所有结构中都存在和、或替代的现象,那么需要进一步思考的是在满足相关语义条件和子集原则的前提下和、或的替代使用是否总是对称的,二者有没有某种使用倾向。接下来本文将对不同结构中和、或替代使用的频数进行数据统计,从而进一步探究二者在使用上的细微差异。
二、不同结构中“和”“或”替代使用的语料考察
(一)语料的来源与筛选
首先,检索北大语料库,在《日出》《太阳照在桑干河上》等现当代文学作品中查找带有和、或的否定结构和量化所有结构。其次,筛选出可以替代的结构或句子,在可替代的结构中统计和、或的使用频数。最后,通过卡方检验计算相关显著性。
(二)不同结构中和、或替代使用的数据统计
下面将从两个角度来统计分析相关数据。一方面,保证同一结构中和、或替代使用的频数足够高,即不限制语料的来源,至少要保证期望频数大于等于5[10],数据统计结果如表1所示。另一方面,在保证同等数量语料的前提下统计不同结构中和、或替代使用的频数,为的是分析二者的替代使用在不同结构中的差异,数据统计结果如表2所示。
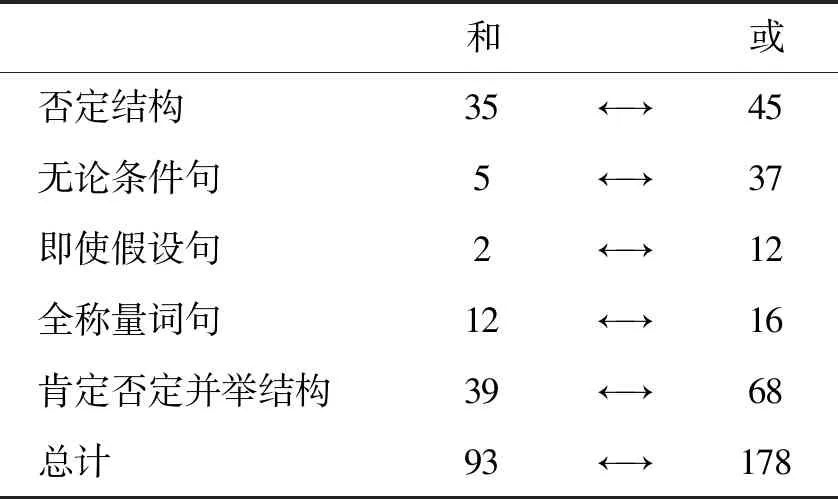
表1 同一结构下和、或替代使用的频数统计③
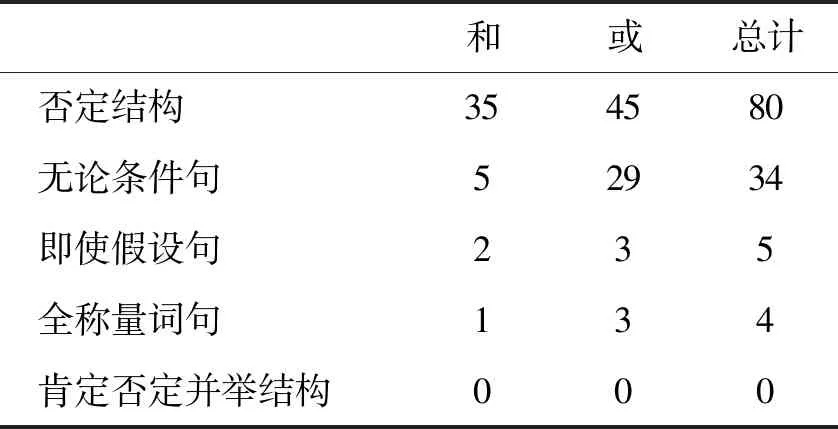
表2 不同结构中和、或替代使用的频数统计
如表1所示,否定结构中虽然使用“或”表示合取的数量多于使用“和”的数量,但二者的使用频数不存在显著差异。通过卡方检验,χ2=1.250且p=0.264>0.01说明在99%的显著水平上二者的替代使用不存在差异。
在无论条件句中χ2=24.381且p=.000<0.01,在即使假设句中χ2=7.143且p=0.008<0.01,这说明我们有99%的把握认为无论条件句、即使假设句中和、或的使用频数存在显著差异。即使统计“无论……还是……”中的“还是”可替换为“和”的情况,“还是”与“和”的使用频数也存在显著差异(p=.000<0.01),但“还是”与“或”的使用频数并不存在显著差异(p=0.166>0.05)。
全称量词句中和、或的使用频数基本一致,二者替代使用的频数无显著差异。需注意的是,虽然肯定否定并举的结构(接纳和/或不接纳都会引发尖锐冲突)中也有全称量化词“都”,但“或”的使用频数显然要高得多,χ2=7.860且p=0.005<0.01说明二者的使用存在显著差异,因此在统计时本文未将这一结构并入全称量词句中。
表1显示在可以替代的结构中“或”的使用频数大致是“和”的两倍,这说明在可以替代的情况下,“或” 出现的频率要更高一些。表2保证了所有结构的语料来源一致,总计一列显示否定结构中和、或替代的情况最多,其次是无论条件句,即使假设句、全称量词句和肯定否定并举结构中替代的现象最少④。χ2=124.057且p=0.000<0.01说明和、或的替代使用在后四种结构中存在显著差异。即使将这四种结构都归为量化所有结构,其与否定结构可替代频数的对比仍然表明二者存在显著差异(p=0.001<0.01)。
总之,否定结构和全称量词句中和、或替代使用的频数不存在显著差异,无论条件句、即使假设句和肯定否定并举结构中和、或的替代使用是不对称的。可替代的情况下,“或”的使用频数要明显高于“和”。否定结构中和、或替代的现象最为常见,无论条件句次之,其他结构相对较少。
(三)不同结构中和、或替代使用的结果分析
否定结构和量化所有结构中和、或替代使用的对称性和不对称性首先与语义辖域有关。否定结构中的“和”不能按照“否定合取”(p∧q)来解释,其对应的解读应从语义辖域上来诠释p∧q。当否定结构中的“或”作子集解读时,“或”可以直接按照“否定析取”来解释,此时它的语义辖域与否定结构中“和”的语义辖域一致。(p∨q)≡p∧q作为一个定律,不仅在汉语中使用,英语中的使用频率甚至更高。Jing[11]指出汉语默认使用“和”来表示合取解读或强解读(strong reading)p∧q,英语默认使用“or”来表示强解读,在不涉及语用因素的情况下,英语否定结构中的“or”更普遍地遵循着德·摩根定律。因此否定结构中和、或替代使用的非显著性与语言中普遍存在的德·摩根定律(p∨q)、否定词和并列连词的语义辖域有关。其次与结构本身的成分有关。在量化所有结构中,全称量化词“都”的使用在一定程度上削弱了和、或之间的差异,使得二者的替代使用未表现出显著差异,这在全称量词句中体现得十分清楚。
虽然全称量化词在削弱和、或的差异上有一定的作用,但在无论条件句、即使假设句中和肯定否定并举的结构中,和、或的使用频数仍然存在显著差异。因此不同结构中和、或使用频数的差异还与标记理论有关。本文认为汉语“和”的使用是无标记的,“或”的使用是有标记的,这基于以下事实:
首先,沈家煊归纳了6条判别无标记项和有标记项的标准,汉语没有形态变化,频率标准和分布标准是比较重要的。[12]Haspelmath从跨语言的角度出发,指出英语的连词“and”以及其他语言中与之对等的连词是使用频率最高的连词,析取连接词在连接名词短语或小句时的限制更少,这可能是由于析取标记使用频率低导致的。[13]“和”的高使用频率和“或”的使用限制表明“和”是无标记的,“或”是有标记的。沈家煊指出经济原则也对有无标记的形成有重要的影响。[12]无标记项的使用频率越高,人们出于经济原则便会在不违反准确表达的情况下采用更加简短的形式。汉语“Neg…和”结构(“不得加以检查和扣留”)句法辖域与语义辖域的不一致正是出于经济原则的考虑,在不违反语义解读的前提下采用无标记的“和”来表达。
其次,汉语史上先有合取连接词,后有析取连接词也可以作为一条证据。吴静、石毓智指出古代汉语中的“与”“且”既可以表示合取,也可以表示析取。[6]虽然上古汉语中就有“或”,但它较早表示的是“有的人”“有时”之意,并不表示析取关系[14-15],如“弃甲曳兵而走,或百步而后止,或五十步而后止”(《孟子·梁惠王上》)。需注意的是,古代汉语中表示合取的连词用的是“与”“而”“且”“及”等,不是“和”。
(8)a. 观书于大史氏。见易象与鲁春秋。(《左传·昭公二年》)
b. 子温而厉,威而不猛,恭而安。(《论语·述而》)
“和”作为并列连词的使用是比较晚的,它大概从晚唐才开始表连带义,后来逐步发展为并列连词。[16]
最后,将“和”的使用看作是无标记的、“或”的使用看作是有标记的,还可以从儿童习得中找到相关的证据。 Notley[17-18]、Gao[19]、Elena[20]假设跨语言的儿童在解读“Neg…and/or”结构时都是一致的,即小孩在理解否定词与合取、析取连接词共现的句子时都倾向理解为否定词取窄域的强解读或子集解读p∧q(强解读要求p和q都为假,整个命题才为真),即使本土语言使用者(成人)倾向理解为弱解读或超集解读(weak/superset interpretation)p∨q(弱解读只要求p或q一个为假,整个命题就为真),当小孩看到大人在特定的情境下将某个句子理解为弱解读时,他也能够基于正面证据积极调整解读倾向。这些研究最终证明跨语言儿童在学习“Neg…and/or”结构时符合Crain提出的语义子集原则(Semantic Subset Principle),即一个句子如果有A、B两种解读,A解读在更狭义的情况下使句子为真(如p∧q),那么在语言的发展过程中,A解读要先于B解读(如p∨q)习得。也就是说,合取或子集解读的习得要早于析取或超集解读的习得。既然小孩是从子集解读开始习得的,那么合取连接词相比于析取连接词要更容易习得。换句话说,p∧q是p∨q的子集,p∧q是p∨q的子集,合取或子集解读是无标记的,析取或超集解读是有标记的。
现在我们可以用标记理论来解释不同结构中和、或替代的不对称现象了。按照标记理论,不同结构中和、或替代使用的频数应该都是有显著差异的,然而二者只有在无论条件句、即使假设句和肯定否定并举的结构中存在差异。对于否定结构和全称量词句来说,和、或之所以未表现出预期的不对称性,这与普遍定律、语义辖域和“都”的差异削弱性有关。对于无论条件句、即使假设句和肯定否定并举的结构来说,这些结构也是默认用“和”来表达的,但因为句中已有了全称量化词或者表示所有义的构式,如果再使用“和”的话,便造成了语义的重复,因此形式上便多采用有标记的“或”来表达。此外“无论”“即使”与“或”共现时,句法上“无论”“即使”取宽域,“或”取窄域,语义则表达为合取解读,这与李占炳所说的英语现象是一致的,他认为英语为了规避否定词和并列结构共现时的辖域歧义问题,否定词后的并列结构往往用“or”而不是用“and”来表示对并列结构的整体否定[8]。这说明英语“or”在否定结构中的使用是有标记的,是为了避免辖域歧义;那么也可以认为汉语“或”在无论条件句、即使假设句中的使用是有标记的,是为了避免语义的重复。
总的来说,不同结构中和、或的替代使用具有不同的表现。否定结构和全称量词句中和、或的替代使用没有显著差异,这与德·摩根定律、语义辖域和全称量化词的差异削弱性有关。汉语“和”的使用是无标记的,“或”的使用是有标记的,按照标记理论,和、或的替代使用在不同结构中都应该存在显著差异,然而只在无论条件句、即使假设句和肯定否定并举的结构中存在差异,这与语义羡余和“或”的标记性有关。
三、结 语
否定结构和量化所有结构中存在和、或替代使用但语义不变的情况。不同结构中和、或的替代与子集原则有关。否定结构、全称量词句中和、或替代使用的频数不存在显著差异,然而在无论条件句、即使假设句、肯定否定并举的结构中,和、或的替代使用存在显著差异。不同结构中和、或替代使用的差异性和非差异性与标记理论、语义内容和全称量化词的特点有关。汉语“和”的使用是无标记的,“或”的使用是有标记的,这可以从频率标准、分布标准、经济原则、历时发展、儿童语言习得等方面得到相关证据的支持。
注释:
②否定结构中的和、或并不总是能够相互替代的,德·摩根定律只能解释可以替代的结构。对于不能替代的结构,如“他不吃苹果或橘子” 在没有语境或上下文的情况下就是个有歧义的句子,既可以理解为他两种水果都不吃,也可以理解为他不吃其中一种。前者可以用德·摩根定律来解释,后者则不能,因为它还可以在后面紧接着说一句“但我忘了他不吃哪一种”。
③箭头表示数据之间存在显著差异。
④肯定否定并举的例子对篇章体裁有一定的选择,表1中可替代的例子主要选自北语语料库中的微博、对话、报刊模块,文学作品中的用例极少。

