数理统计在计量检测中的应用

李慧轩

（鲁东大学 数学与统计科学学院，山东 烟台 264000）

计量、标准、检验检测和认证认可，是组成国家质量的基础设施。在经济社会的发展过程中，质量控制和质量管理涉及社会的各个方面。计量和检验检测过程中出现的各种数据，是实现质量控制和质量管理的重要抓手之一。如何对这些数据进行科学分析和运用，并通过数据分析结果，进行趋势或走向的预测和判断，是加强质量控制、实现有效管理的重要手段。

一、数理统计的基本概念

数理统计是一门统计分析科学，是统计学发展到一定阶段的产物。简而言之，数理统计是分析数据的一种方法，通过对随机现象进行有限次的观测和记录，对得到的有限数据进行分析、计算，了解事物内在规律，进而对事物的整体规律进行判断和把握。可以说，数理统计是认识事物、把握事物、利用事物的良好工具[1][2][3]。

二、数理统计在计量检验中的常用术语

计量是保证单位统一、量值可靠的活动。传统的计量是指计量技术机构对常用计量器具进行周期性检定，或者依据客户需求完成校准，是完成仪器量值溯源、确保仪器测定准确的重要手段。现代意义上的计量不仅是局限于末端计量器具的检定和校准，而是贯穿于产品生产的全过程、全链条、全寿命周期的计量，是关于测量和应用的一门学科。一台正常使用的仪器，一个产品的生产过程、使用周期，其量值溯源包含多个步骤，但最终都离不开数据计算和数据处理。在计算和处理过程中，会用到数理统计的各个表征量。

（一）示值误差

化学计量中，仪器测量值的示值误差一般有三种表示方式：绝对误差、相对误差和引用误差。绝对误差是指测量值与真实值之间的差值；相对误差是指测量值与真实值的差，再除以真实值；引用误差是指测量值与真实值的差，再除以仪器的满量程。因为真实值难以获得，一般以多次测量的算术平均值作为真实值。上述三种示值误差的计算公式如下：

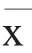
（二）测量重复性

一般而言，测量重复性是指测量结果的分散性。按照《通用计量术语及定义》中的定义，测量重复性是指在相同测量程序、相同测量系统、相同操作条件和操作地点下，短时间内对同一被测量对象重复测量，所得测量结果的一致性。多次测量的重复性一般以标准偏差s表示。测量重复性是引起测量不确定度的重要因素之一，在测量不确定度的评定中，常被当作A类不确定度的评定。其计算方法有极差法和贝塞尔公式法。

极差法：保持测量条件不变的情况下，对某一被测量对象进行n次独立测量，得到的一组测量结果中，最大的测量值与最小的测量值之差，称为极差，用R表示。当测量次数比较少时，在测量不确定度的计算中，若采用极差法计算测量重复性，s=R/C，式中的C为极差系数，是与测量次数相关的数值，通过查表可获得。

（三）测量不确定度

测量不确定度简称不确定度，是与测量结果相关联的一个参数，用于表征合理赋予被测量的值的分散性。测量不确定度的评定和计算步骤复杂，可以分为A类评定和B类评定。其中A类评定是指在规定测量条件下，测得的量值用统计分析的方法进行的测量不确定度分量的评定，主要是指测量重复性。B类评定是指除A类评定方法以外的其他不确定度评定方法，其评定主要基于标准物质的量值、校准用标准器的准确度等级、仪器分辨率、人员推断的经验值等等。A类、B类不确定度整合为合成不确定度，再乘以给定的包含因子（通常取k=2），就得到最终的扩展不确定度。

测量不确定度的来源是多方面的，如被测量的定义不完整、重复测量的方法不理想、取样的代表性不够、被测量受环境或温度的影响、测量标准器的分辨率不高、标准物质定值引入的不确定度，等等。值得一提的是，测量不确定度与测量误差有根本区别。测量不确定度与人们对被测量的认识及影响测量的过程有关，表示测量结果的分散性，是一个非负参数。而测量误差表示的是测量结果与真实值的差异，是一个有正有负的量值，其来源有系统误差和偶然误差。

三、计量校准中数据分析与应用实例

以概率论为基础理论，根据试验结果和观察随机现象得到的数据资料，对随机现象进行研究，这个过程能体现数理统计的特点。本文以煤矿束管监测系统红外线气体分析仪的一次校准为例，说明数量统计在仪器计量校准与检测中的应用。

煤矿束管监测系统主要用于煤矿井下自然气体的监测，整个监测系统主要由束管、抽气泵、流量控制系统、气相色谱仪、红外线气体分析仪等组成。其中气相色谱仪用于检测C2H2、C2H4、C2H6的含量，红外线气体分析仪用于 CO、CO2、CH4、O2的测量。相比于早期单纯的气相色谱法测量，由气相色谱仪联合红外线气体分析仪共同完成自然气体测量，具有分析时间短、线性范围宽、相互干扰少、可24小时连续分析等优点[8]。

（一）t检验法

通过聚乙烯材质的束管，利用真空泵将井下布置的各监控点的气体抽至地面，先后进入气相色谱仪和红外线气体分析仪，完成各种气体成分的分析。对各路流量计进行校准，通过多路流量计控制进样气体流量，是保证仪器测量数据准确性的前提。按照《浮子流量计检定规程》的要求，进行转子流量计检定时，检定流量点的设定按照规程中所述：在流量计的流量范围内，选择包括上限流量和下限流量在内的不低于5个均匀分布流量点进行检定。束管监测系统控制面板上所用转子流量计的量程为3L/min，根据转子流量计自身分度值设置，选择 0.3L/min、0.5L/min、1.0L/min、1.5L/min、2.0L/min、2.5 L/min等6个点进行校准。

对转子流量计采用标准表法进行校准，选择的气体介质和实验分析时所用的气体标准物质相同。将被检流量计串联安装在标准流量计的下游（也可以是上游），以标准流量计的读数为准，依次调节设定其流量值为 0.3L/min、0.5L/min、1.0L/min、1.5L/min、2.0L/min、2.5L/min，当标准流量计和被检流量计的流量达到稳定时，记录被检流量计的读数，连续测量7次，数值如表1所列：

表1 被检流量计的测量结果

以0.3 L/min的校准点为例，用数理统计的方法对校准结果进行分析，属于单样本的t检验问题。对表1中0.3L/min点的7次测量值进行计算，显著性水准α取0.05，单次测量的标准偏差和t值分别为：

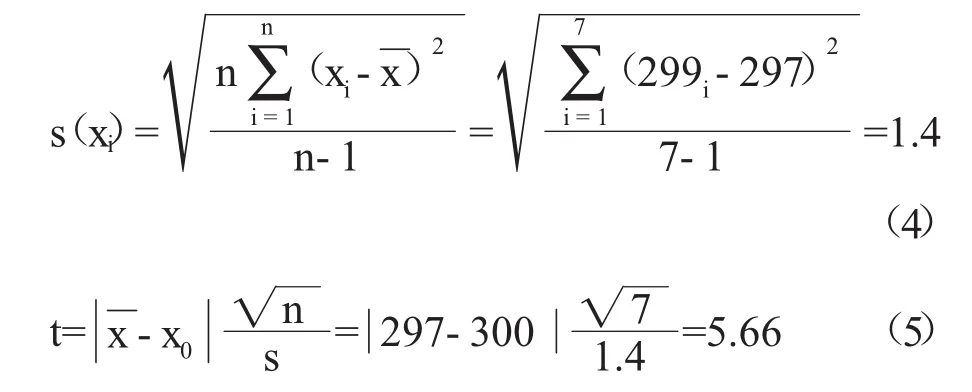
综上所述，丙泊酚镇静辅助硬膜外麻醉能够降低患者的心理和生理应激指标，明显缓解患者焦虑情绪，提高患者的舒适度及对麻醉的满意程度。

（二）F 检验法

束管监测系统内，进样气路控制面板中一般有4个进样口，可以采用球胆进样，也可以通过流量控制器控制标准气体钢瓶压力，然后直接进样。现以CO气体标准物质为例（浓度为1530 ppm），校准红外线气体分析仪，考察不同进样口和不同进气方式是否有显著差异。

采用F检验判断两次测量结果间是否存在显著差异，通过比较任意两组数据的方差s2，得到一个F值，然后取置信度为95%（即显著性水平为0.05），查表得到一个F表值，比较F值和F表的大小。若F值＜F表，则认为两组数据间无显著性差异，否则认为它们之间存在显著性差异，即存在系统误差，需要找出原因，加以解决[9][10]。

式中，s表示样本标准偏差。

1.仪器不同进样口校准测量结果的F检验

分别对4个不同进样口通入同一种气体标准物质，重复测量7次，得到的仪器示值和相对偏差列于表1。

2.同一进样口不同进样方式校准测量结果的F检验

针对4个不同的进样口，分别以气瓶连接直接进样和球胆进样两种方式对仪器进行校准，重复测量7次，得到的仪器示值和标准偏差列于表2中。

表2 不同进样口、直接连接CO标准气体气瓶仪器的测量值（ppm）

表3 同一进样口、分别连接气瓶和球胆时仪器的测量值（ppm）

观察表2中的数据，选择单次测量标准偏差较大的一组，即4#进样口，计算其F值。

采用同样的顺序和步骤，分别用CO2、CH4、O2标准气体进行实验，发现ULTRAMAT23型红外线气体分析仪的示值均无显著性差异。

四、结语

统计是认识和描述客观事物、解决问题的一种方法。统计学产生于应用，在应用过程中发展壮大。在化学计量工作中，统计更是发挥着不可替代的作用，一切检定、校准的测量结果，都需要进行统计计算，才能有效表明仪器量值是否准确，生产过程、终端产品质量是否得到有效控制。开发合理的校准方法和科学的统计计算，是实现计量技术服务、助推产业高质量发展的重要保障。

数理统计不仅在工程技术、产业发展中有着极为广泛的应用，而且在人文社会观察与规划、社会经济运行判断与决策等多方面都有不可忽视的作用。未来，随着经济社会的不断发展以及学科相互交叉融合，统计学会吸收和融合相关学科的新理论，不断开发出新技术和新方法，以满足人们对于系统及系统复杂性认识的要求，统计学的应用领域、统计理论与分析方法必将不断发展，在更多领域展现生命力和重要性。◆