方差累积和控制图的改进
郭莹莹
(燕山大学 理学院,河北 秦皇岛066004)
一、引言
控制图的提出,最初目的是对过程均值是否发生变化进行监控,之后逐渐用于过程方差的监控,因为尽管产品质量与目标值相差不大,其方差也具有较小幅度的偏移。在产品生产过程中,由于系统因素,样本在均值特性上可能没有明显变化,但在方差特性上会有很大偏移,如果方差的偏移量超出了规定要求,就必须对过程方差进行监控,过程方差增加会导致产品质量降低。当前对过程方差监控最普遍使用的控制图是休哈特(Shewhart)R图,S图和S2图。传统的休哈特控制图在过程发生比较大的偏移时敏感,在发生小偏移和中等偏移时不敏感。另外,当样本容量很小时,监控工艺效率低下。为了优化这些问题,学者们研究了带有运行规则的监控过程方差的控制图。
为了提高过程方差发生中、小偏移时监控的灵敏度,Page E S[1]于1954年提出了累积和控制图,一些数理统计学专家先后对累积和控制图进行了深入研究。Guoyi Zhang[2]针对传统休哈特S图的不足,提出了修正的S图,并介绍了改进的休哈特R图和S图;Rakitzis和Antzoulakos C等[3]提出了监测过程方差的运行和控制图;薛丽[4]对累积和控制图的参数K和H进行了研究和分析,讨论了基于三种不同原则的参数选取方法;胡灵雪和王志远等[5]建立了同时监控均值和方差的累积和控制图,提出基于马尔可夫链理论的新控制图的平均运行链长计算方法;孙明超和宋向东等[6]提出基于累积和控制图改进的累积得分控制图,设置改进控制图的初始响应值,改进了控制图与传统累积和控制图比较方法;杨静和宋向东等[7][8]对方差控制图进行改进,检测效率明显提高。
对于方差发生小波动的生产过程,累积和控制图相比休哈特控制图的监控效率更高。过程方差一旦发生小的偏移,累积和控制图就能迅速检测出来。在产品制造过程中,累积和控制图是一种很有效的监控工具。因此,对它的优化尤为重要。传统的休哈特控制图是在3σ原则上建立的,而累积和控制图是以序贯概率比检验为依据的。本文将累积和控制图与常规控制限联合使用,基于累积和方法,加入了常规控制限思想,根据总体服从正态分布时的方差特性设置了上控制限系数,并讨论了上单侧联合的常规-累积和S2图的平均运行链长表现,有效地提高了监控方差向上偏移的灵敏度,这在监控过程方差方面有一定的借鉴作用。
二、累积和控制图原理
(一)累积和控制图原理—序贯概率比检验

下面给出一个重要命题:
在使用时可近似取
其中α为犯第一类错误的概率即当H0为真时拒绝H0的概率;β为犯第二类错误的概率即当H0不真时接受H0的概率。
(二)累积和控制图的常用方法
1.截顶V型模板法

截顶V型模板运用于实践中,操作比较容易。决定截顶V型模板的形状有两个参数:f和h,f称为参考值,h称为判定距。如图1所示,f是截顶V型模板边界的斜率,h是截顶V型模板中点O处垂直高度的一半。

图1 截顶V型模板示意图
判断过程方差是否发生偏移时,把截顶V型模板放在累积和控制图上,中心点O与最新得到的点重合,直线OA与样本序号轴平行。若之前描的点均在透明模板的两条斜线内,则判断过程方差没有发生异常偏移;若有一点恰好在截顶V型模板的下斜线上或超出下斜线则判断过程方差异常增大;若有一点恰好在截顶V型模板的上斜线上或超出上斜线,则判断过程方差异常减小。
2.列表法
监控过程偏移的累积和控制图可看作重复的序贯概率比检验,构造累积和控制图的两个参数为K和H,K称为参考值,H称为决策值。检验过程方差是否发生偏移是检验统计量是否落入原假设H0的拒绝域。
监控过程方差向上偏移的累积和控制图检验统计量表达式为:
D+m=max{0,D+m-1+sm2-K},初始值 D0+=0
当D+m>H时,说明过程发生了向上的偏移,拒绝原假设H0,控制图发出警报,停止抽样。
(三)控制图的性能指标ARL
对于控制图,通常称从过程检测开始到它发出失控的报警信号为止,抽取的平均样本组数为平均运行链长(ARL)。
平均运行链长是评价累积和控制图性能优劣的一个重要指标,设计控制图时一般都希望在过程受控时平均运行链长不低于预设值,在过程失控时平均运行链长越小越好。要比较不同控制图的性能,通常是固定受控时的平均运行链长,失控时的平均运行链长较小的控制图控制性能更加优良。常用的计算平均运行链长的方法有马氏链法、积分方程法和随机模拟法,本文采用随机模拟的方法计算平均运行链长。
三、上单侧联合的常规-累积和S2图
在过程方差的监控中,过程方差增大说明产品的合格率下降。在某些产品的生产过程中,原材料劣质、机器零件不合格或磨损、操作工人操作失误等都会造成过程方差变大。可以使用上单侧联合的常规-累积和S2图监控过程方差向上的偏移,尽快发出警报,提高生产过程性能。
(一)上单侧联合的常规-累积和图设计
设过程质量特性X∶N(μ,σ2),样本量大小为m。我们希望当过程方差σ2由σ02偏移到σ12(σ12=ρσ02,ρ>1为偏移倍数)时,控制图能尽快发出警报。为了检验过程方差向上的偏移,将常规控制图上控制限(UCL)思想加入到累积和控制图中,取当前的观测值即样本方差si2,检验si2是否大于Bσ02,其中σ02是已知的过程方差,B为上常规控制限系数。如果si2不大于Bσ02,就将其按惯例加入累积和,如果 si2大于 Bσ02,则发出状态失控的信号。
上单侧联合的常规-累积和S2图将0直限作为控制下界,0直限到控制限上界的距离为控制距H,0直限到警戒限的距离为警戒距K。横轴表示样本组序号m,纵轴表示样本方差si2(i=1,2,3,…,m)与警戒距K的的累积和Cm(K)。设初始值为0,则有累积和:
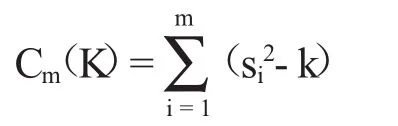
(二)上常规控制限的确定
下面计算上常规控制限系数,计算过程中将系数记为B。
当过程上偏时,不发出失控信号的的随机事件表示为S2 若用F(x)表示自由度为n-1的卡方分布的概率分布函数,则发出失控信号的概率为: p=p(ρ)=1-F[(n-1)(B/ρ)] 平均运行链长即为L(ρ),对于错误报警率α=0.002,当ρ=1即过程方差处于受控状态时,平均运行链长L(ρ)有 L(1)=500,计算 S2统计量的上常规控制限系数结果如表1: 表1 不同样本容量的上常规控制限系数表 将上述求得的控制限系数作为上单侧联合的常规-累积和S2图的上控制限系数,即先检验每组的样本的S2统计量是否大于Bσ02,若大于此值则发出报警信号,不大于此值则按上述标准计入累积和。 假定观测值服从正态分布,且总体均值相同,即xi∶N(μ,σ2),i=1,2,3,…。用 f表示概率密度函数,则两个假设可表示为: H0:σ02~f(σ02),i=1,2,3,… H1:σi2~f(σ12),i=1,2,3,… 第m次抽样,从而H1对H0的似然比为: 其中,K为上参考值,H为决策值。 可以定义上偏的联合的常规-累积和s2图的检验统计量为: zj=max{0,zj-1+sj2-K},j≥1 用下面的标准来判断检测过程是否正常: 1.检验 sj2是否大于 Bσ02,如果 sj2大于 Bσ02,则发出状态失控的信号,如果sj2不大于Bσ02,就将其按惯例加入累积和; 2.当Cm(K)≤0时,认为过程方差波动正常,但此阶段累积和计算中断,接下一个阶段的累积和计算; 3.当0 4.当Cm(K)≥h,认为过程方差向上偏移,发出报警信号。 采用随机模拟方法计算平均运行链长,并绘制平均运行链长曲线与传统的方差控制图的比较: 从表2可以看出,当过程方差发生上偏时,上单侧联合的常规-累积和S2图较传统的方差控制图有较短的平均链长,说明对于方差向上偏移的过程,上单侧联合的常规-累积和S2图检测效率优于传统的方差控制图。 表2 n=10时过程上偏的联合的常规-累积和S2图平均链长表现 图2 上单侧常规-累积和S2图与传统的方差控制图平均链长比较 图中给出了n=10时偏移从1倍到3倍时上单侧联合的常规-累积和S2图与传统的方差控制图平均链长比较,当方差偏移倍数在1.1倍到1.6倍间可以看出上单侧联合的常规-累积和S2图具有优越性,当方差偏移倍数大于2.5倍时,上单侧常规-累积和S2图几乎立即报警,说明联合的常规-累积和图在检测较小偏移时有较高灵敏性。 本文研究过程方差检测的累积和方法,将累积和控制图与常规控制限联合使用,基于累积和方法,加入了常规控制限思想。利用随机模拟方法计算联合的常规-累积和S2图的平均链长,并与传统的方差控制图的平均运行链长进行比较。结果发现,联合的常规-累积和S2图在检测向上偏移的方差过程具有更高灵敏性。因此,它的进一步研究是有实际价值的。◆

(三)上单侧联合的常规-累积和S2图检验统计量





(四)平均运行链长表现


四、结论

