WOD随机变量序列加权和的完全收敛性
章茜,蔡光辉
(1.浙江机电职业技术学院数学教研室,浙江杭州310053;2.浙江工商大学统计与数学学院,浙江杭州310018)
0 引 言
在统计学中,最小二乘估计、密度核估计、递归密度核估计、非线性核估计等统计量均为随机变量加权和形式,对随机变量加权和极限性质的研究很重要。在实际应用中,考虑独立性假设的不合理性,很多相依结构被相继提出。因此,研究相依结构的随机变量序列具有一定的理论和实际意义。
WANG等[1]提 出 了 宽 相 依(widely orthant dependent,WOD)随机变量序列概念,其定义为:
定义1[2]如果存在有限的实数序列{gU(n),n≥1},任取n≥1和xi∈(-∞,+∞),1≤i≤n,满 足P(X1>x1,X2>x2,…,Xn>xn)≤为上宽相依(widely upper orthant dependent,WUOD)随机变量序列;如果存在有限的实数序列{gL(n),n≥1},任取n≥1和xi∈(-∞,+∞),1≤i≤n满足

则称{Xn,n≥1}为下 宽相依(widely lower orthant dependent,WLOD)随机变量序列;如果{Xn,n≥1}既是WUOD随机变量序列,又是WLOD随机变量序列,则称{Xn,n≥1}为WOD随机变量序列,其控制系数记为g(n)=max{gU(n),gL(n)}。
WOD随机变量序列是较负相依(negativelyorthant dependent,NOD)序 列 和 扩 展 负 相 依(extended negatively dependent,END)序列[2-6]等更为广泛和一般的随机变量序列。自WOD随机变量序列概念提出以来,众多学者对其进行了研究,如蔡光辉等[7]在独立随机变量序列重对数律基础上,获得了不同分布WOD随机变量序列的重对数律;丁洋等[8]获得了WOD随机变量加权和的完全收敛性;TAO等[9]获得了WOD随机变量序列滑动平均的完全收敛性;LIU等[10]获得了WOD随机变量序列的矩完全收敛性;YAN[11]研究了负宽相依(WNOD)随机变量序列的几乎处处收敛性及在非参数模型中的应用;WU等[12]在R-h-可积条件下获得了WOD随机变量序列的一些极限性质。
完全收敛性的概念最先由HUS等[13]提出并进行研究,其在强大数定律和强收敛速度研究中具有十分重要的作用。CHEN等[14]获得了一类NOD随机变量加权和的完全收敛性,其结果为
定 理1[14]设1<α≤2,α<γ,{X,Xn,n≥1}
为同分布的NOD随机变量序列,且EX=0,E|X|γ<∞。设实数三角阵列{ank,1≤k≤n,n≥1}满足
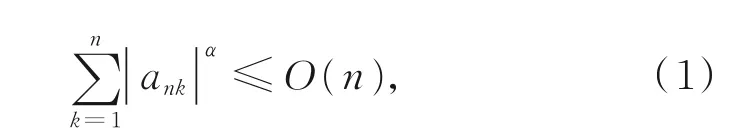
则

本文将定理1推广至WOD随机变量序列的情形,在证明方法上亦与传统的先对随机变量进行截尾的方式有所不同。
定 理2 设1<α≤2,α<γ,{Xn,n≥1}是WOD随机变量序列,且被随机变量X所控制,满足EX=0,E|X|γ<∞,控 制 系 数 为g(n)=(logn)αγ(1+δ),δ>0。设实数三角阵列{ank,1≤k≤n,n≥1}满足式(1),则对任意的ε>0,式(2)成立。
注1 定理2将定理1推广至WOD随机变量序列的情形,定理1是定理2的特例。
注2 与定理1相比,定理2取消了同分布这一条件。
注3 文献[8]研究的是经典的Baum-Katz型完全收敛性,定理2研究的是尾为n1α(logn)1γ形式的完全收敛性,是对Baum-Katz型完全收敛性的拓展。
本文中,C表示正常数,在不同情形下值可能不同。an≪bn表示an=O(bn),而an=O(bn)表示an≤Cbn,记logx=ln max{x,e},#A表示集合A中包含的元素个数。
1 定理的证明
为证明定理2,需要以下引理。
引理1[2]设{Xn,n≥1}为WOD随机变量序列,如果{fn(⋅),n≥1}为均非升(或均非降)函数,则{fn(Xn),n≥1}仍为WOD随机变量序列。
引理2[16]设随机变量序列{Xn,n≥1}被随机变量X所控制,则对任意的v>0,x>0,n≥1,有
(i)E|Xn|vI(|Xn|≤x)≤C{E|X|vI(|X|≤x)+xvP(|X|>x)};