无人机位置控制循迹算法设计及仿真*
◆殷惠莉 宋淑然 薛秀云 林景峰 姚俊光
0 引言
MATLAB是当前国际最流行的面向工程、数值和科学计算的高级语言。MATLAB环境下的Simulink拥有丰富的系统建模、仿真和分析动态仿真环境工具箱[1]。华南农业大学电子工程学院的各个专业都有开设MATLAB仿真课程,但是学生大多是根据课程教学要求按部就班学习,没有非常明确的目的,缺乏学习动力,学习效果一般。为充分利用虚拟仿真技术创新工程实践教学方式,进一步培养学生基于模型设计的思想和解决问题的能力,让学生了解前沿行业信息,全面提高学生的综合能力,指导学生参加MATLAB杯全球(中国赛区)大学生无人机竞赛。该竞赛是由MathWorks发起的无人机竞赛,旨在帮助学生在毕业前了解工业界先进的基于模型设计理念,并学习行业通用的标准软件。基于模型设计的方法正在改变工程师和科学工作者的工作方式,用建模仿真试验替代实物测试试验,可缩短工程设计时间与成本。
无人机是一种空中飞行器,无须安装飞行员相关设备,通常受控于无线电遥控或自身程序。当前,无人机正呈现智能化和集群化发展态势,各种无人机正渐渐进入公共服务体系,在军用和民用领域广泛应用,比如执行侦察、通信、精确打击等军事任务,航拍、城市管理、农业等民用任务[2]。
从系统角度看,无人机是一种多输入输出的欠驱动系统[3]。无人机的控制是通过输入四个可控变量来控制飞行时的六个自由度。可控变量对无人机的控制存在强耦合,易受干扰,这就造成其飞行控制十分困难。为了满足无人机的稳定循迹,汪勇等[4]采用激光雷达扫描识别高压电线,使得无人机随高压线的走向进行循迹,但是激光雷达检测容易造成点云数据缺失、噪点多、建模复杂等缺点[5]。同时,这种方法只能识别突出的物体,对于平面线段无法识别。蔡鑫等[6]采用摄像头捕获轨道图像,将整个图像分割成五个区域,根据五个区域的像素点的信息特征来识别路径,但是因为采用了大部分像素,增加了算法开销,同时还有可能引进错误的像素,从而增大算法的复杂度。无人机采用摄像头提取预期位置值时,其细微的姿态偏移可能会引起较大的预期位置的偏差。
本文在总结不同轨迹的图像特征的情况下,设计一种复杂度低且能稳定循迹的算法,这种算法提取部分像素,分析得出轨迹,通过位置控制实现循迹。
1 图像处理算法设计
视觉循迹的基本思路是通过区分图像中不同轨道的特征来判断轨迹。为了尽量减轻硬件开销,本文均采用灰度图分析。在一个灰度图像中,如果灰度局部发生剧烈变化,则以此为基础检测边缘。
二值化灰度图像后,算法通过基于一阶导数的Sobel边缘检测算法提取灰度图边缘。该算法引入类似局部平均的运算,对噪声具有平滑作用,能很好地消除噪声的影响。经过Sobel算法边缘检测模块处理后,可以输出图像的两个不同方向的梯度分量:一个是Gv垂直边缘梯度响应矩阵,即纵向边缘,该矩阵只显示竖线,为竖线矩阵;另一个是Gh水平边缘梯度响应矩阵,即横向边缘。
提取灰度图像边缘后,通过矩阵提取图像中某一行或者一竖的像素点,将多维信息转化为一维信息。经过以上数据处理后的一维矩阵中,只有有限个元素的值是非零的。这些元素的个数定义为特征点个数,这些非零元素的下标数值定义为特征点的值。
提取轨迹轮廓需要重点关注轮廓边缘和噪声点,噪声点[7]包括孤立点、端点、交叉点。通过提取像素矩阵后,轨道轮廓边缘具有连续性,会持续影响循迹决策。不具有连续性的噪声点很难对循迹算法造成持续干扰,从而可以忽略其不良影响。
位置控制与姿态控制之间存在耦合。为了达到解耦控制的目的,李斌斌等[8]设计了一种甲烷型过驱动四旋翼无人机。这种通过改变无人机的结构达到解耦控制目的的方法,增大了硬件的开销。在无人机姿态变化较小的情况下,为了消除耦合带来的影响,本文提出一种方法——斜线补偿。这种方法可以在不用引入硬件的情况下,在一定范围内消除位置变化和姿态变化引起的误差。
当发生耦合的时候,通过斜线补偿可以计算出由于姿态变化而引起的误差。误差值的计算公式如式(1)、式(2)所示,其中,Ex、Ey为计算出来的误差,K1与K2分别为解耦系数,X、Y分别表示X轴、Y轴上的实际值,pitch与roll分别对应各自姿态角弧度。

解耦系数依据实际调试时测试得到。该方法可以在一定程度上解决由于姿态变化而带来的影响。由于位置变化而引起的误差,其值可以通过式(3)、式(4)计算。

其中,Exs、Eys分别为X轴和Y轴上计算出来的误差,这个值会与预期值累加;W为轨道此时的宽度;Kxs、Kyx为X轴和Y轴上的误差系数,是一个正数。轨道的宽度可以根据特征点的值计算所得。要特别注意,如果无人机偏移轨迹不超过半个机身,就不需要计算其引起的误差。
综上所述,图像处理算法流程如图1所示,其中轨道此时在图像中所占像素点个数为L1。摄像头在轨道正上方时,轨道在图像中所占像素点个数为L2。
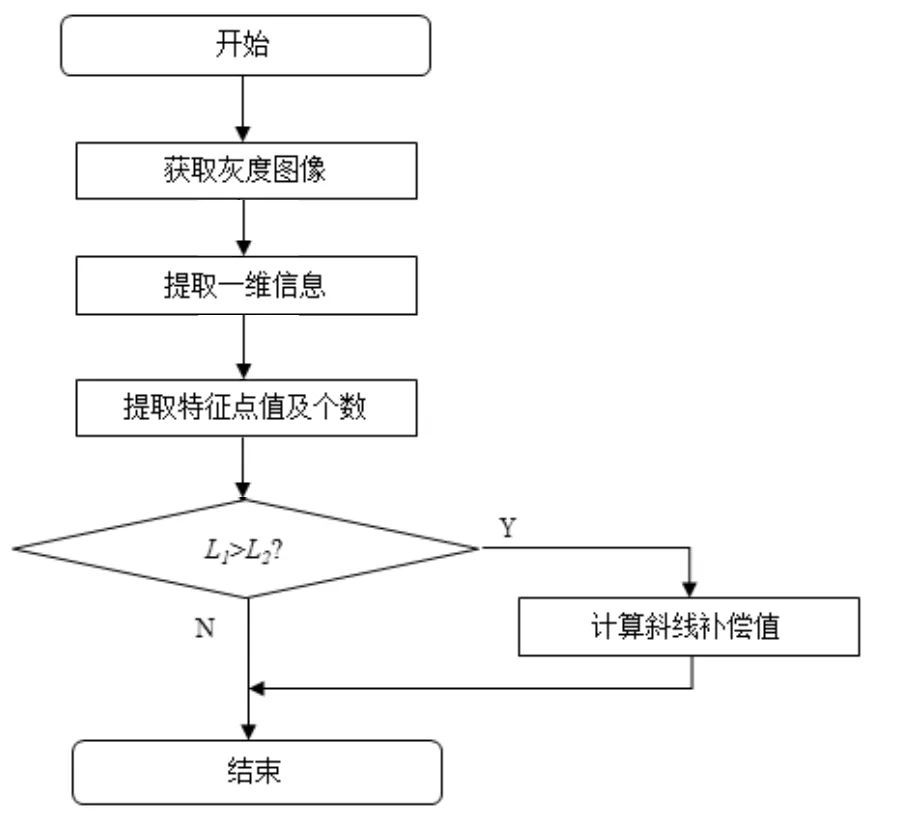
图1 图 处理流程
2 循迹算法设计
为了发掘各种轨道的共性及特性,需要从根本上分析各种轨道的不同之处。为了操作方便,将无人机的运动先简单地分为四种情况。同时从特征点个数的变化这个方面来考虑不同轨道的不同特征。
基本方向 如果不考虑高度变化,就可以将无人机运动的方向简单分为向前、后、左、右四个基本方向,其中向前为实际坐标中X轴的正方向,向右为实际坐标中Y轴正方向。斜线循迹可以看为两个方向上的运动的叠加。横向矩阵指的是沿着X轴垂直的方向通过矩阵提取图像中某一行的像素点。竖向矩阵指的是沿着Y轴垂直的方向通过矩阵提取图像中某一竖的像素点。
横向矩阵提取出来的特征点的信息可以反映实际坐标中X轴的变化,竖向矩阵提取出来的特征点的信息可以反映实际坐标中的Y轴的变化。如果要完成向左向右的基本方向的运动,采用横向矩阵时,可以向左向右运动,采用竖向矩阵可以向前向后运动。假如这里采用横向矩阵特征点,那么如果Y轴以固定距离输出,则无人机可以完成向左和向右两个基本方向,同时会根据特征点来调整在实际坐标中X轴的运动。向前向后的运动可以此类推。表1列出基本方向对应的运动方法。注意:该表中的X、Y轴为实际坐标轴。

表1 基本方向采用的不同矩阵及固定距离
基本运动 通过总结归纳,循迹的路线类型可以分为直线、钝角弯道、直角弯道、锐角弯道、圆弧。表2列出了这五种基本运动的特征点信息,从特征点个数的角度分析五种路线类型。从特征点个数的变化可知,直线和钝角弯道可以视为一种情况,圆弧和直角弯道有一段是相同的,它们都有从两个点变为一个点的过程,要保证转弯后可以继续走,就需要在两个点变为一个点时,采用另外一个矩阵提取出来的特征点。比如无人机要从向前转为向右,就要从采用竖向矩阵的特征点变为采用横向矩阵的特征点。锐角弯道最为特殊,会有从三个点变为两个点的过程,可以在这个过程发生时进行矩阵的切换。
转弯只会发生在横向矩阵与竖向矩阵切换时,而每一次切换都会有特征点的消失。因此,当采集到的图像信息表示需要矩阵切换时,就计算出上一个采样时间到这一个采用时间里丢失的点,以该点作为下一个需要逼近的目标,当逼近时,由于惯性,无人机会先继续保持原来的运动方向运动一段时间,这样完成转弯过程。
基本模式 在无人机飞行的过程中有四种飞行模式:
第一种是向前横切模式,即规定与无人机机体垂直的方向为横切,并且向前运动;
第二种是向后横切模式,即与无人机机体垂直的方向为横切,并且向后运动;
第三种是向左竖切模式,即规定与无人机机体平行的方向为竖切模式,并且向左运动;
第四种是向右竖切模式,即与无人机机体平行的方向为竖切模式,并且向右运动。
设置这四种不同的飞行模式是为了当轨道发生变化时无人机能及时作出调整,即由横切模式切换到竖切模式,或者由竖切模式切换到横切模式,或者做前后/左右模式的切换。其中横切的标志位是0或2,竖切的标志位是1。
基于以上分析,循迹算法流程如图2所示。其中初始化过程是确定最初的基本方向的过程。在初始化过程中分别采用横向矩阵和竖向矩阵,选取特征点个数最多的矩阵为初始基本方向。初始化只会在刚起飞的时候执行,执行一次后就不再执行。

图2 循迹算法流程
3 模型仿真
用Simulink设计轨道,轨道如图3所示,其中轨道宽度为100 cm,图中箭头所指方向为无人机起点。当直线与摄像机坐标中X轴平行时,特征点为48、69;当直线与摄像机坐标中Y轴平行时,特征点为62、83。无人机起飞稳定后,摄像机以200 ms为周期拍摄图片,图片矩阵大小为120×80。无人机高度固定为1.1 m,起飞到机身稳定高度所需要的时间为1.6 s,这段时间内完成初始化。仿真中Y轴对应的斜线补偿误差系数Kys为0.3,X轴对应的斜线补偿误差系数Kxs为0.1。解耦系数K1、K2均为0.35。如果解耦系数过大,无人机姿态很难发生改变,遇到转弯等轨道就无法正常循迹。如果误差系数过大,那么在循迹斜线的时候就会导致无人机剧烈晃动。解耦系数和误差系数太小,就无法达到解耦控制的目的。

图3 轨道图
图4所示为飞行仿真过程中,无人机在X轴和Y轴上与飞行原点的距离,正值表示沿轴正方向,负值表示沿轴负方向。由图4可以看出:在0~20 s内,在X轴上的距离直线上升,Y轴的则保持不变,此时无人机正沿着图4中第一段轨道循迹;在20~21 s完成直角转弯之后,在21~40 s内沿着第二段轨道循迹,此时在X轴上的距离保持不变,Y轴的则直线上升。在循迹最后一段斜线的时候,两轴实际距离均减小。整个过程仿真时间为83.88 s,飞行总距离为8.8 m,平均速度为0.105 m/s。
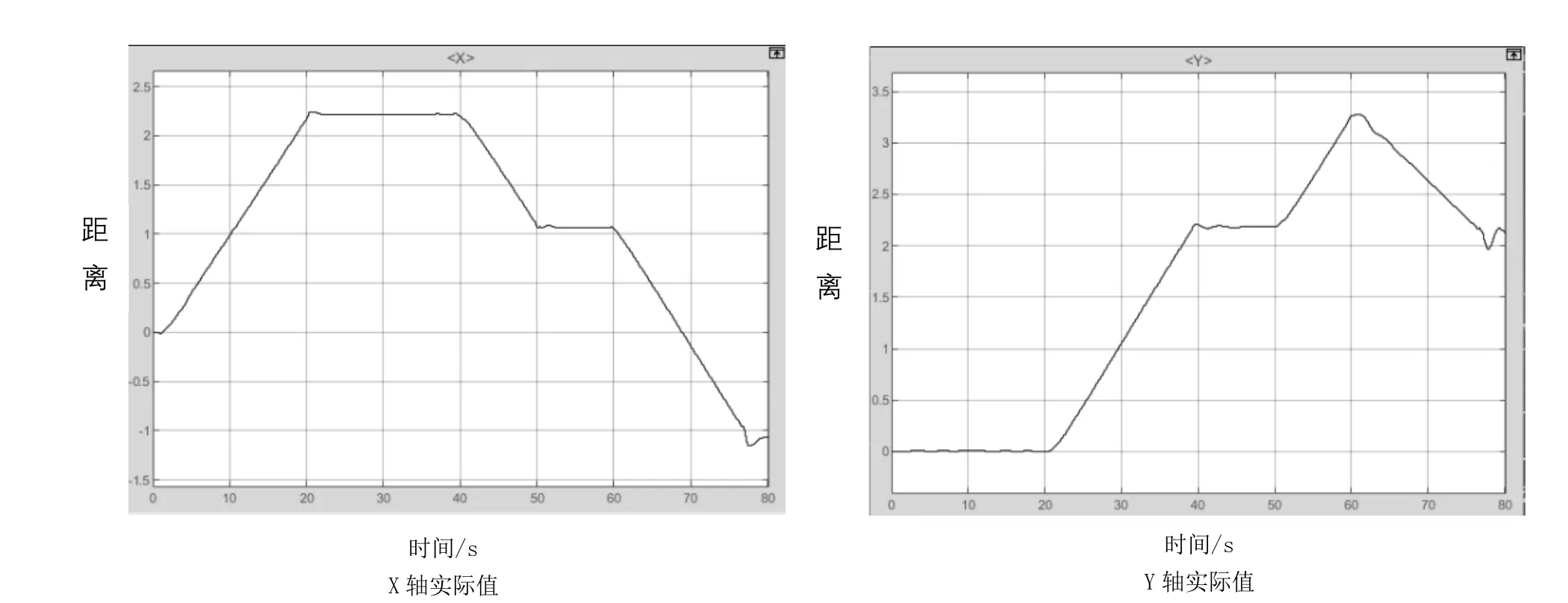
图4 轨道各轴实际值
图5所示为仿真飞行过程中的部分截图,整个过程无人机基本不偏离轨道,证实了该算法的可行性。图6为未采用斜线补偿时,无人机循迹斜线时的状态,可以看出此时无人机大部分机身已经偏离轨道。而在图5所示的整个循迹过程中,即使是循迹幅度比较大的斜线,也有超过一半的机身是在循迹线上的,有力证实了斜线补偿的有效性。

图5 采用斜线补偿算法仿真图

图6 未采用斜线补偿算法仿真图
4 结语
本文提出的基于图像分割的无人机位置控制循迹算法,可以通过采集图像中的极少部分像素来达到循迹的目的,减少其他有误差的像素造成的干扰。同时采用斜线补偿的方法在一定程度上消除由于位置控制和姿态控制耦合引起的误差。最后通过Simulink,完成包括前进、后退、转弯等情况的循迹仿真,效果良好。参与比赛的学生都表示,无论是否获奖,大家都通过大赛锻炼了自己的团队协作和沟通能力,充分认识到虚拟仿真技术的强大,掌握了图形化仿真的方法,初步了解到基于模型设计理念,激发了学习兴趣,找到了学习方向,更坚定了继续深入学习实践的信念。

