水面舰艇反潜防御中无人潜航器兵力需求研究 *
戚学文,夏青峰,王相
(中国人民解放军91776部队,北京 100161)
0 引言
随着智能化无人技术的发展及其在军事领域的应用,各军事大国充分认识到无人作战系统对于完善装备体系,乃至改变未来战争模式所具有的重大意义[1-2]。其中,舰载无人潜航器可同时携带主被动声纳、声纳浮标等多种搜潜设备[3-6],在大型舰艇周围形成隐蔽的反潜警戒屏障,根据需求为大型舰艇提供一定范围的反潜防护[7-9],且由于无人潜航器与敌方潜艇同处水下介质,较其他反潜兵力具有天然优势。但由于大型舰艇在执行远海作战任务时,自身可搭载无人潜航器的数量规模有限,因此在满足作战需求的前提下明确无人潜航器搭载数量规模,是对有限作战资源充分、合理利用的有效途径。本文以大型舰艇平台航渡中对潜防御问题为牵引,研究舰载无人潜航器在构建反潜防御屏障时的数量需求及其主要影响因素,对未来大型主战舰艇无人潜航器搭载方案及舰载无人潜航器性能的设计,充分合理利用舰载无人作战资源具有一定参考价值。
1 兵力配置基本要求
大型舰艇作为海上高价值目标,是潜艇攻击的最主要目标之一。鱼雷武器作为潜艇主要进攻手段,具有隐蔽突然、毁伤威力大等特点,为此大型舰艇在航渡中要确保安全通过潜艇威胁海区,必须构建严密的对潜防御屏障。其兵力配置的基本要求[10]为:①要根据受敌潜艇威胁扇面的大小,将警戒兵力环形或半环形配置在舰艇周围,构成严密覆盖敌潜艇鱼雷攻击威胁扇面的反潜屏障;②反潜防御区内反潜兵力的警戒扇面必须有一定的重叠,以保证反潜屏障的严密性。
基于上述要求,无人潜航器在使用中一方面需前出配置,做到先敌发现,并在敌潜艇占领鱼雷攻击阵位实施攻击前,引导大型舰艇发射反潜武器消灭敌潜艇[11-13];另一方面要基于现代核动力潜艇水下机动速度快,目标舰艇可能遭受全方位攻击的特点,综合考虑大型舰艇搭载无人潜航器数量限制,力求以最少无人兵力为大型舰艇构建严密的全方位反潜屏障。
2 兵力机动要素分析
编队航渡过程中,总体要求是多艘无人潜航器组成全方位环形防御圈,机动部署在目标舰周围一定范围海域,遂行对潜探测任务,保证在敌潜艇占领鱼雷攻击阵位之前,引导目标舰对其实施攻击。
定义1 潜艇攻击阵位线。受鱼雷武器航程的限制,潜艇发射鱼雷能够在其最大有效航程内命中目标的最远位置线。
定义2 无人潜航器最迟警戒线。为保证无人潜航器在敌潜艇占领攻击阵位前引导目标舰对其实施攻击,要求无人潜航器探测到敌潜艇的最迟界线。
如图1所示,O1为敌潜艇位于无人潜航器最迟警戒线时目标舰的相应位置点,O2为敌潜艇位于攻击阵位线时目标舰的相应位置点,O3为敌潜艇发射鱼雷命中目标舰的位置点。

图1 敌我机动要素分析图Fig.1 Maneuver elements of both sides
图1中,为满足作战要求,无人潜航器反潜屏障须在敌潜艇到达“最迟警戒线”之前对其发现,并在敌潜艇到达“攻击阵位线”之前引导目标舰对其至少完成1次有效攻击。需要指出的是,无人潜航器最迟警戒线并不是规则的圆形轨迹,下面通过建模对其进行解析计算。
3 兵力需求问题建模
由上述分析可知,无人潜航器兵力需求与所要构建的无人潜航器反潜屏障密切相关,而无人潜航器反潜屏障由敌潜艇攻击阵位线、无人潜航器最迟警戒线确定。因此,需首先以敌我双方作战平台机动要素与武器性能参数为输入,对敌潜艇攻击阵位线、无人潜航器最迟警戒线进行解析计算。为此,根据敌我双方机动要素建立几何解析模型,如图2所示。
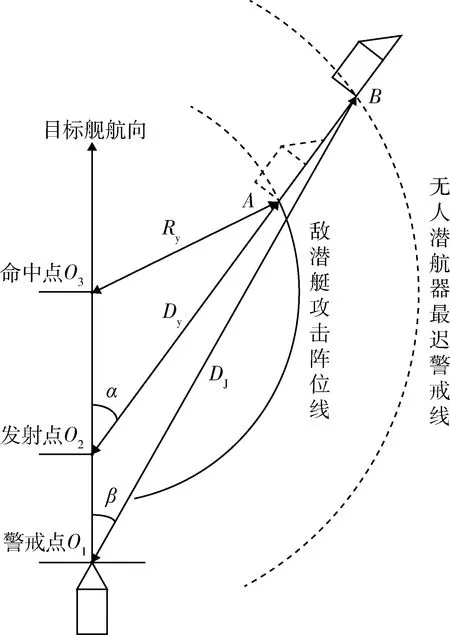
图2 无人潜航器反潜屏障几何解析图Fig.2 Anti-submarine barrier provided by unmanned underwater vehicles
考虑到水下平台的深度数值远远小于潜艇发射鱼雷最大有效射距Dy以及无人潜航器最小警戒距离DJ,因此在建模过程中忽略深度因素的影响。
3.1 敌潜艇攻击阵位线的确定
根据定义1,敌潜艇攻击阵位线即敌潜艇对目标舰发射鱼雷武器的位置线。设敌潜艇采用前置点射击模式。当目标舰位于图1中O2点时,敌潜艇于攻击阵位线某点占领阵位发射鱼雷,于O3点命中目标舰。忽略目标舰运动的情况下,敌潜艇攻击阵位线通常可认为是以鱼雷发射点O2为圆心,以鱼雷最大有效航程Ry为半径的圆。但由于鱼雷在水中航行速度与舰船航速差距不够显著,因此不能忽略鱼雷航渡过程中目标舰的运动[14],不考虑目标舰发现来袭鱼雷并作出相应战术机动(虽然实际作战中这种情况较少出现,但如此处理并不影响本文对问题的研究),鱼雷对目标舰的命中点O3应位于目标舰航向上O2点前方某点,并不与O2点重合。于是,需对潜艇位于目标舰O2点不同舷角时发射鱼雷的最大有效射距Dy进行求解[15]。

式中:Ry为鱼雷最大有效航程(通常取其最大航程Sy的80%);vy为鱼雷发射后航行速度;vj为目标舰运动速度。
由平面几何和三角函数解析可得:
α∈[0°,360°],
式中:α为鱼雷发射阵位A相对于目标舰相应位置点O2的舷角。
根据前文对敌潜艇攻击阵位线的定义,其可描述为当α∈[0°,360°]取值时,由与O2点距离为Dy的点构成的曲线。于是,由Dy的表达式即可确定敌潜艇攻击阵位线。
3.2 无人潜航器最迟警戒线的确定
如图2所示,对于敌潜艇而言,当其到达无人潜航器最迟警戒线上某点B后(此时目标舰位于O1点),最优机动方案为尽快到达攻击阵位线占领阵位对目标舰实施攻击,无人潜航器最迟警戒线与敌潜艇攻击阵位线间隔即为敌潜艇从最迟警戒线到达攻击阵位线间航线相对于目标舰前置点O2的径向距离。
设T为编队反应时间,即无人潜航器自发现敌潜艇至引导目标舰发射攻潜武器命中所需的时间,则:
T=T1+T2+T3,
式中:T1为无人潜航器发现并跟踪识别敌潜艇的时间;T2为无人潜航器识别敌潜艇后将目标信息传输给目标舰的时间;T3为目标舰接收信息后实施打击至武器命中敌潜艇的时间。
用vq表示敌潜艇占领阵位航渡速度,分析可知,敌潜艇从最迟警戒线到达攻击阵位线间航线相对于目标舰前置点O2的径向距离最大值为vq·T,此时敌潜艇沿其在最迟警戒线上位置点B与O2点连线方向机动至攻击阵位线,其攻击阵位即为该连线与敌潜艇攻击阵位线的交点(图2中A点)。于是,将敌潜艇攻击阵位线上某点沿其与O2点连线方向外推vq·T距离,即为该点对应的无人潜航器对敌潜艇最迟警戒位置点,由此基于敌潜艇攻击阵位线即可得到无人潜航器最迟警戒线。
无人潜航器最迟警戒线上某点到目标舰位置点O1的距离,设为在该方向上无人潜航器最小警戒距离,用DJ表示[16]。显然,DJ是一个与目标舰航速,潜艇航向、航速,潜艇初始阵位以及编队反应时间等因素相关的变量。由图2解析分析,DJ可表示为
DJ=vj·T·cosβ+
β∈[0°,360°],
式中:β为敌潜艇被发现时相对于目标舰当前点O1的舷角。
根据前文对无人潜航器最迟警戒线的定义,其可描述为由与O1点距离为DJ的点构成的曲线。于是,由DJ的表达式即可确定无人潜航器最迟警戒线。
3.3 无人潜航器数量需求模型
对潜防御无人潜航器的配置阵位,可由每一艘无人潜航器相对于O1点的配置方位φ和前出距离DQ表示。为便于描述,不妨假设每艘无人潜航器对潜有效探测距离相同,均为dw。则只有当无人潜航器探测圆全部覆盖其对潜最迟警戒线时,才能保证全方位反潜防护的严密性,确保目标舰安全。此时,每一艘无人潜航器有效探测圆与最迟警戒线有2个交点,该2个交点的连线即为无人潜航器有效探测圆的一条弦,显然其长度最大值即为圆的直径2dw。可知,当每一艘无人潜航器有效探测圆与最迟警戒线的交点C,D的连线恰好是其探测圆的直径,并且相邻无人潜航器有效探测圆所对应的交点连线首尾相接时,全部覆盖最迟警戒线所需的无人潜航器有效探测圆数量最小,即目标舰对反潜防御无人潜航器的数量需求也最小,如图3所示。
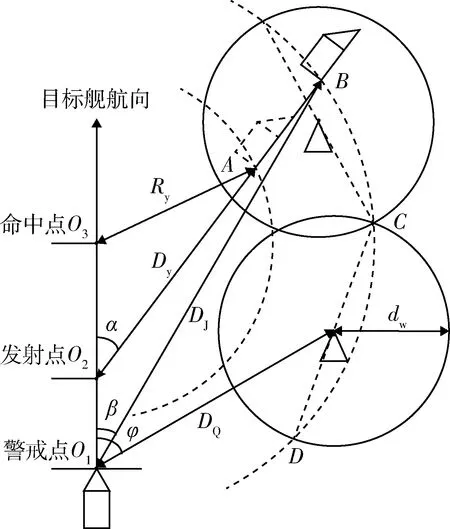
图3 无人潜航器数量需求解析图Fig.3 Number required of unmanned underwater vehicle
由于无人潜航器有效探测圆直径与最迟警戒线长度差距显著,可认为每个有效探测圆与最迟警戒线2个交点间所对应的最迟警戒线劣弧曲率较小。因此,目标舰对反潜防御无人潜航器的最小需求数量N可由最迟警戒线周长与有效探测圆直径的商进行估算。要求N的值为整数,且根据前文反潜兵力配置基本要求,为保证反潜屏障的严密性,无人潜航器警戒扇面必须有一定的重叠,因此应将估算结果向上取整。
于是,无人潜航器最小需求数量N可表示为
式中:L为无人潜航器最迟警戒线周长;[·]为取整函数。
由上述建模过程可以看出,舰载无人潜航器最小需求数量的影响因素包括目标舰运动速度vj,敌潜艇占领阵位航渡速度vq,鱼雷发射后的航行速度vy,鱼雷最大有效航程ry,编队反应时间T以及无人潜航器对潜有效探测距离dw,下面通过案例分析对各因素的影响情况进行量化计算,并由计算结果找出其中的主导因素。
4 案例分析
以上述各项影响因素为已知输入,计算无人潜航器最迟警戒线周长、无人潜航器最小需求数量,并分析每项因素对无人潜航器最小需求数量的影响情况。其中,敌潜艇设置为攻击型高速核潜艇。
4.1 参数设置
参考现有各类典型装备(武器)性能,设置对应参数值,作为模型计算的基本输入。具体为:vj=20 kn,vq=24 kn,vy=25 kn,Ry=30 n mile,T=0.4 h,dw=10 n mile(1 n mile=1.852 km,1 kn=1.852 km/h)。为分析其中某个变量对舰载无人潜航器最小需求数量的影响情况,令其他变量取值不变(取基本输入参数值),对指定变量设置取值区间。取值区间的设置,应考虑目前对应类别装备(武器)性能,力求涵盖其大多数型号的性能参数范围。
4.2 仿真数据
根据文中模型,应用Matlab R2019a软件进行仿真计算,得出无人潜航器最迟警戒线周长以及无人潜航器最小需求数量的计算结果。
(1) 目标舰运动速度vj影响分析
根据解析计算模型可知,当vj>vy时,Dy无实数解,导致L亦无实数解。因此设vj∈[10,24] kn,步长取2 kn进行计算,L与N的计算结果如表1所示。

表1 目标舰运动速度影响计算结果Table 1 Results affected by surface vessels’ velocity
为便于比较,将表1中数据绘制曲线,如图4所示。
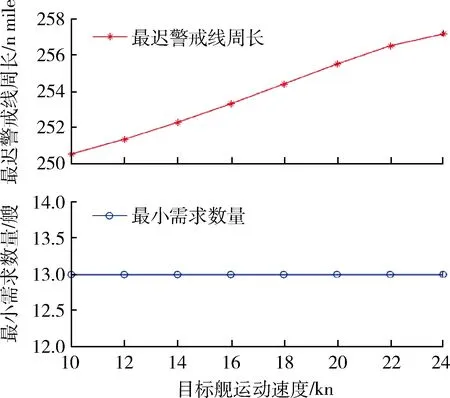
图4 目标舰运动速度影响趋势Fig.4 Trendline affected by surface vessels’ velocity
可见,无人潜航器最小需求数量N对目标舰运动速度vj的变化并不敏感,当vj取值在10~24 kn时,N的值恒为13艘,变化幅度为0。亦即,当目标舰运动速度vj增大2.4倍时,无人潜航器最小需求数量N不变。
(2) 敌潜艇占领阵位航渡速度vq影响分析
设vq∈[16,36] kn,步长取2 kn进行计算,L与N的计算结果如表2所示。
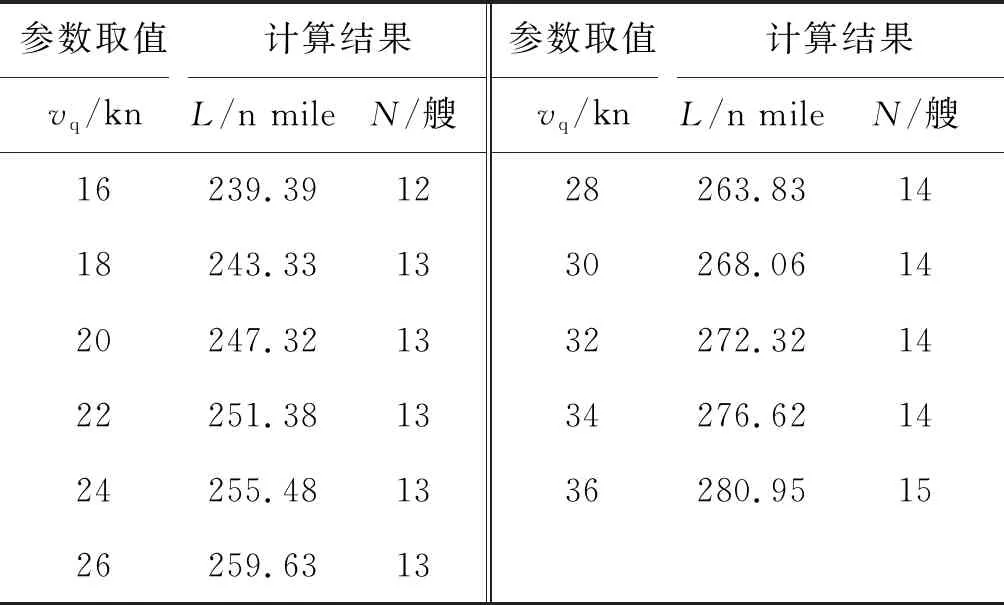
表2 敌潜艇占领阵位航渡速度影响计算结果Table 2 Results affected by enemy submarines’ velocity
为便于比较,将表2中数据绘制曲线,如图5所示。

图5 敌潜艇占领阵位航渡速度影响趋势Fig.5 Trendline affected by enemy submarines’ velocity
可见,敌潜艇占领阵位航渡速度vq对无人潜航器最小需求数量N的影响较为明显,当vq取值从16 kn增大至36 kn时,N的值从12艘增加到15艘,变化幅度为3。亦即,当敌潜艇占领阵位航渡速度vq增大2.25倍时,无人潜航器最小需求数量N增加25%。
(3) 鱼雷发射后的航行速度vy影响分析
设vy∈[20,40] kn,步长取2 kn进行计算,L与N的计算结果如表3所示。

表3 鱼雷发射后的航行速度影响计算结果Table 3 Results affected by torpedoes’ velocity
为便于比较,将表3中数据绘制曲线,如图6所示。
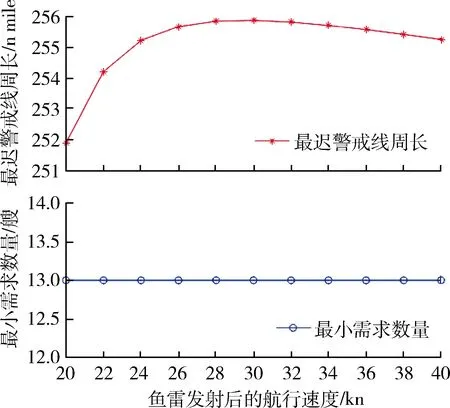
图6 鱼雷发射后的航行速度影响趋势Fig.6 Trendline affected by torpedoes’ velocity
可见,无人潜航器最小需求数量N对鱼雷发射后的航行速度vy的变化并不敏感,当vy取值为20~40 kn变化时,N的值恒为13艘,变化幅度为0。亦即,当鱼雷发射后的航行速度vy增大2倍时,无人潜航器最小需求数量N不变。
(4) 鱼雷最大有效航程Ry影响分析
设Ry∈[20,40] n mile,步长取2 n mile进行计算,L与N的计算结果如表4所示。
为便于比较,将表4中数据绘制曲线,如图7所示。

表4 鱼雷最大有效航程影响计算结果Table 4 Results affected by torpedoes’ maximum effective range

图7 鱼雷最大有效航程影响趋势Fig.7 Trendline affected by torpedoes’ maximum effective range
可见,鱼雷最大有效航程Ry对无人潜航器最小需求数量N的影响相当显著,当Ry取值从20 n mile增大至40 n mile时,N的值从10艘增加到16艘,变化幅度为6。亦即,当鱼雷最大有效航程Ry增大2倍时,无人潜航器最小需求数量N增加60%。
(5) 编队反应时间T影响分析
设T∈[0.2,1.0] h,步长取0.1 h进行计算,L与N的计算结果如表5所示。

表5 编队反应时间影响计算结果Table 5 Results affected by reaction time
为便于比较,将表5中数据绘制曲线,如图8所示。

图8 编队反应时间影响趋势Fig.8 Trendline affected by reaction time
可见,编队反应时间T对无人潜航器最小需求数量N的影响相当显著,若T取值从0.2 h增大至1.0 h,N的值从12艘增加到18艘,变化幅度为6。亦即,当编队反应时间T增大5倍时,无人潜航器最小需求数量N增加50%。
(6) 无人潜航器对潜有效探测距离dw影响分析
设dw∈[2,20] n mile,步长取2 n mile进行计算,L与N的计算结果如表6所示。

表6 无人潜航器对潜有效探测距离影响计算结果Table 6 Results affected by unmanned underwater vehicles’ effective detection range
为便于比较,将表6中数据绘制曲线,如图9所示。
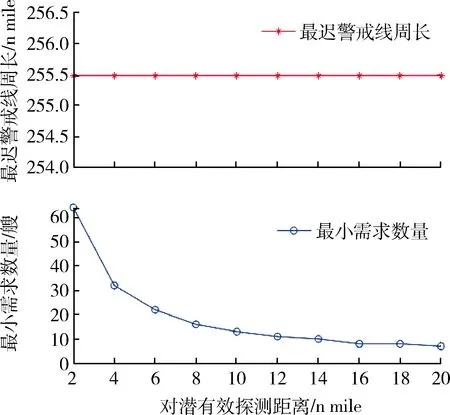
图9 无人潜航器对潜有效探测距离影响趋势Fig.9 Trendline affected by unmanned underwater vehicles’ effective detection range
可见,无人潜航器对潜有效探测距离dw对其最小需求数量N的影响非常剧烈,当dw取值从2 n mile 增大到20 n mile时,N的值从64艘骤减至7艘,变化幅度为57。亦即,当无人潜航器对潜有效探测距离dw增大10倍时,无人潜航器最小需求数量N减少89.06%。且当dw取值在10 n mile以下变化时,其对无人潜航器最小需求数量N的影响尤为剧烈。
4.3 结果分析
由仿真数据结果可以看出,在各类典型装备(武器)性能参数合理变化范围内,6项影响因素中,无人潜航器对潜有效探测距离dw对其最小需求数量N的影响最为剧烈,为1级主导因素;鱼雷最大有效航程Ry、编队反应时间T为无人潜航器最小需求数量N的2级显著影响因素;敌潜艇占领阵位航渡速度vq为无人潜航器最小需求数量N的3级次要影响因素;目标舰运动速度vj、鱼雷发射后的航行速度vy为无人潜航器最小需求数量N的4级非敏感影响因素。
在大型主战舰艇无人潜航器搭载方案设计方面,除考虑能够满足舰艇周围环形配置数量需求外,还应主要考虑dw,Ry,T3项因素,适当考虑vq的影响;在舰载无人潜航器性能设计方面,应注重增大其对潜有效探测距离,同时力求缩短跟踪识别、目标信息传输时间以减少其最小需求数量,使得载舰有限的搭载能力最大程度满足对潜防御需求。尤其是当舰载无人潜航器对潜有效探测距离水平较差时,更要引起注意。
5 结束语
本文针对水面舰艇航渡过程中,依靠舰载无人潜航器构建反潜防御屏障的兵力需求问题展开研究。基于敌我兵力机动要素分析,建立了敌潜艇攻击阵位线、无人潜航器最迟警戒线解析模型以及舰载无人潜航器最小需求数量估算模型。通过仿真计算,对6项影响因素进行分级,进而从大型主战舰艇无人潜航器搭载方案设计与舰载无人潜航器性能设计两方面提出建议。文中方法逻辑性强,算法复杂度低,便于操作,具有较强的可行性。下一步研究中,①考虑在目标舰发现来袭鱼雷并作出相应战术机动的情况下,进一步完善建模及计算方法;②探索载舰与无人潜航器水下协同探测、协同防御的建模,以期降低对载舰搭载能力的需求。

