放射性气载流出物浓度分布的影响因素分析
何堂将 李敏 孙世杰 刘旭东 于成波


摘 要:核设施运行时不可避免地会产生和排放出放射性气载流出物,气载流出物进入大气后将发生扩散,因此,掌握放射性气载流出物在扩散过程中浓度分布的影响因素是开展环境评价和辐射防护工作的基础和前提。现利用高斯烟羽模型,在高架源源强恒定条件下,分析大气稳定度、风速、地形等因素对近地面气载流出物浓度的影响。计算结果表明,大气越稳定,近地面浓度越小,最大浓度点距离越远;风速越大,近地面浓度越小,但最大浓度点距离不变;地区下降地形会使近地面浓度小于水平地形的浓度,并使最大浓度点距离增加。
关键词:反应堆;气载流出物;浓度;影响因素
0 引言
气载流出物自高架排风塔释放出来进入大气后,在大气湍流的作用下,迅速同周围大气混合,在横向及垂直方向上做无规则运动,这个过程称为“大气扩散”。在扩散的同时,放射性物质在风场的作用下随风运动,这个过程称为“输送”。气载物在大气中的扩散和输送过程称为“大气弥散”。放射性物质进入大气后在大气弥散时受到气象条件、地形、污染物本身的物理/化学性质等诸多因素影响,过程极其复杂,很难用严格的数学模型进行准确描述。目前主要基于统计理论、K理论和相似理论,在对实际扩散过程进行简化的基础上,开发了多种大气弥散模型[1]。其中,针对正常及事故工况,最常用模式为高斯烟羽模型,该模型可在多种气象条件下估算放射性物质释放到大气后下风向各点浓度,其有效性已得到实验验证。
本文拟采用高斯烟羽模型[2-3],对高架排风塔释放的放射性气载流出物在大气弥散过程中浓度分布的影响因素进行研究,计算得出大气稳定度、风速、地形对放射性气载流出物在大气中浓度的影响,为环境评价和辐射防护工作提供理论支持。
1 研究方法
1.1 模型建立
高斯烟羽模型是由湍流统计理论导出的正态分布假设下的一种扩散模式,也是目前应用最为广泛的一种大气扩散模型。它的求解需满足以下几个假定条件[4]:(1)湍流扩散为菲克扩散;(2)污染源强是连续的、均匀的;(3)在整个计算区域和计算时间内,风速、风向和大气稳定度恒定;(4)污染物质量不变,地面对污染物全反射。污染物在顺风方向两侧服从正态分布,且在顺风方向风对污染物的运输远远大于湍流引起的污染物扩散。
根据以上假设,可得出有风时连续点源的浓度扩散的高斯模型:
X(x,y,z)=exp-
+
(1)
式中:X(x,y,z)为在排风口下风向(x,y,z)点处的核素浓度(Bq/m3);Q为源释放的速率(Bq/s);u为平均风速(m/s);σy、σz分别为水平和垂直方向的扩散系数。
在实际应用时,大部分污染源是高架源,在弥散过程中存在地面反射作用,所以大气中的放射性气载物浓度一方面是排放口的贡献(实源),另一部分是地面反射的贡献(虚源)[5]。
(1)实源的贡献为:
X1(x,y,z)=exp-
+
(2)
(2)虚源的贡献为:
X2(x,y,z)=exp-
+
(3)
式(2)与(3)中H为烟羽释放有效高度(单位:m)。
实际浓度X(x,y,z)=X1(x,y,z)+X2(x,y,z),可得到高架连续点源扩散的高斯烟羽模型表达式:
X(x,y,z)=exp-
2·
exp-
+exp-
令z=0,便可得到地面浓度公式:
X(x,y,0)=exp-
2exp-
(5)
式中:X(x,y,0)为下风向x m、横向y m处的地面空气浓度(Bq/m3)。
1.2 扩散系数
大气稳定度是影响扩散的重要因素,是确认大气扩散的基础。根据帕斯奎尔(Pasquill)分类法将大气稳定度分为A、B、C、D、E、F六个等级,分别对应强不稳定、不稳定、弱不稳定、中性、较稳定、稳定,再由布里格斯提出的经验公式得出扩散系数与其对应。扩散系数如表1所示。
1.3 烟羽释放有效高度
烟羽抬升高度主要受烟羽与环境的温差及烟羽初始动能的影响。气载流出物的温度(17 ℃)与排风塔出口处的环境温度相差不大,因此不考虑温差的影响。仅考虑烟羽初始动能时,烟羽抬升高度可用Rupp方程计算:
Δh=1.5Vd/ (6)
式中:Δh为抬升高度(m);V为排风塔出口烟羽初速度(m/s);d为排风塔出口内径(m);为排风塔排出口处平均风速(m/s)。
考虑排风塔的高度H0,则烟羽释放的有效高度为:H=H0+Δh。
1.4 气象条件
计算地区属中亚热带湿润季风气候,选取地区气象站2018-04-01至2019-04-01间完整一年的气象观测资料。气象塔高45 m,基底海拔为525.4 m,设有地面、20 m、40 m三个观测梯度。观测期间平均气压95 300 Pa;平均風速0.67 m/s,瞬时风速极大值为6.7 m/s。
2 影响因素分析
2.1 大气稳定度
高架排风塔高度H0=125 m,排风塔出口内径d=2 m,排风塔出口排气速度V=5 m/s,平均风速=0.67 m/s,假设排风塔气载物源强Q=1×106 Bq/s,并假设高度为近地面。
根据公式(6)求得抬升高度Δh≈22.4 m,有效高度H=147.4 m。再根据公式(5)令y=0,可求得稳定度为A~D类气象条件下(E、F稳定度对地面浓度影响作用小,此处不考虑)近地面轴线方向上的浓度分布,如图1所示。
图1中,A类:最大值点坐标(524 m,14.98 Bq/m3);B类:最大值点坐标(877 m,12.5 Bq/m3);C类:最大值点坐标(1 461 m,11.0 Bq/m3);D类:最大值点坐标(4 198 m,5.1 Bq/m3)。其中,下风向距离为近地面点到排风塔的距离。由此可知,A~D类大气稳定度条件下,近地面放射性气载流出物浓度随下风向距离的增加,先增大再逐渐减小,大气越稳定,近地面浓度越小,最大浓度点距离越远。
2.2 风速
风速为0.67 m/s、1.1 m/s和6.7 m/s时,选择A类大气稳定度条件,其他情况与2.1节相同。根据公式(6)求得对应的有效高度H,并结合公式(5)令y=0,求得不同风速下的放射性气载流出物浓度,如图2所示。
图2中,风速为0.67 m/s、1.1 m/s和6.7 m/s时,近地面放射性气载流出物最大浓度分别为14.98 Bq/m3、9.1 Bq/m3和1.5 Bq/m3。由此可知,随着风速增加,近地面各点的浓度减小,近地面最大浓度点与排风塔的距离不变。
2.3 地形因素
天气稳定时,假定烟羽中心始终保持海拔高度不变,则污染源的高度为H-ht(H为有效源高,ht为评价点海拔与排放塔基底海拔之差),实源与虚源形成的浓度为:
X(x,y,z)=exp-
2·
exp-
+exp-
计算的地形呈下降趋势,简化来看,如图3所示,排风塔底部到最低落地点的直线距离约2 km,海拔差为-140 m。中间点的距离为800 m,中间平台长400 m,海拔差为-70 m。
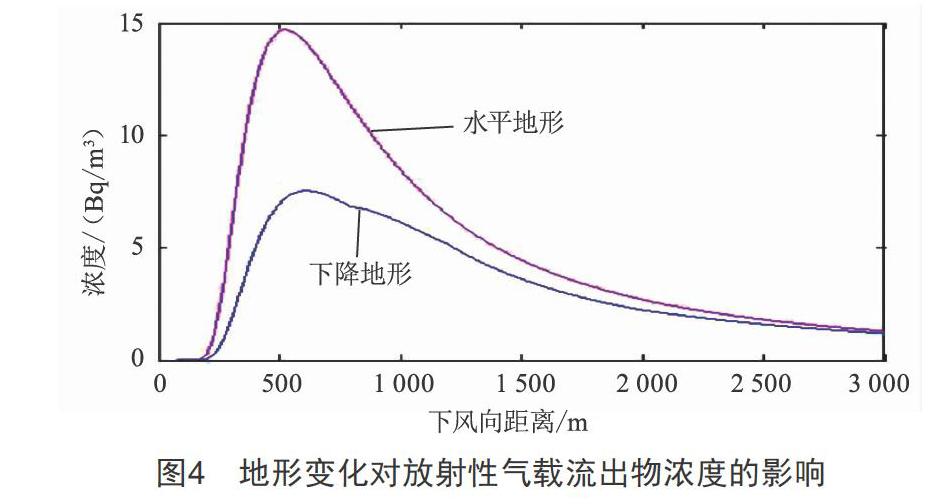
假设风速取0.67 m/s,A类大气稳定度条件,其他情况与2.1节相同。由公式(6)求得相应的有效高度H,并根据公式(5)令y=0和公式(7)令y=0与z=0,分别求得水平地形与下降地形情况的放射性气载流出物浓度,如图4所示。在水平地形时,最大值点坐标(524 m,14.98 Bq/m3);在下降地形时,最大值点坐标(614 m,7.7 Bq/m3)。由此可知,下降地形的近地面放射性气载流出物最大浓度值较水平地形小,距离较水平地形远。
3 结论
本文运用高斯烟羽模型对排风塔周边地区放射性气载流出物浓度分布的影响因素进行研究,得出如下结论:(1)在大气稳定度分别为A~D类时,大气越稳定,近地面放射性气载流出物浓度越小,最大浓度点与排风塔的距离越远。(2)随着风速的增加,近地面各点的浓度减小,近地面最大浓度点与排风塔的距离不变。(3)下降地形的近地面放射性气载流出物最大浓度值较水平地形小,与排风塔的距离较水平地形远。这些结论对于进一步研究放射性气载流出物浓度分布,为环境评價和辐射防护工作提供理论支持具有重要意义。
[参考文献]
[1] 姬文超.核电站气载放射性核素浓度和辐射剂量计算[D].广州:暨南大学,2008.
[2] 王淑莹,张良,崔晓哲,等.基于高斯烟羽模型的热电厂对空气质量影响案例分析[J].环境监控与预警,2020,12(4):28-32.
[3] 孙涛,汪根宝.利用高斯烟羽模型设计尾气放空烟囱的探讨[J].化工设计,2020,28(1):12-15.
[4] 刘爽.核设施事故排放气载放射性污染物扩散模拟研究[D].哈尔滨:哈尔滨工程大学,2017.
[5] 张兵.放射性物质大气弥散仿真研究[D].哈尔滨:哈尔滨工程大学,2004.
收稿日期:2021-03-23
作者简介:何堂将(1989—),男,广西凌云人,硕士研究生,工程师,研究方向:反应堆运行。

