基于BPNN-TD算法的城市轨道交通线网规模预测方法

靳旭刚，陈德玖，黄 丽，周天宠，杨立晨

（1.重庆市市政设计研究院，重庆 400020；2.北京交通大学海滨学院，河北沧州 061199；3.北京交通大学交通运输学院，北京 100044）

1 研究背景

随着我国经济的跨越式发展以及城镇一体化建设的加快，居民的职住分布情况恶化，交通拥堵等问题接踵而来。轨道交通系统以运量大、运距长、速度快等特点，得到了相关交通部门和出行者的青睐。因此，许多城市正在建设以轨道交通为主导的城市综合交通体系。而以公共交通为导向(TOD)的城市发展模式的不断推进与“公交都市”项目的不断落地[1]，也使得轨道交通在我国各大城市的客流运送任务中日趋重要。

当前，许多城市在“地铁热”的浪潮下大力建设轨道交通。截至2018年，中国已有近40个城市开通轨道交通。为了更加科学合理地推进国内各省市轨道交通的建设，近年国家开始逐渐缩紧对轨道交通建设的审批，提高建设门槛。在当前城市轨道交通建设的关键时期，如何全面掌握影响轨道交通发展的内外部因素，精准预测与城市结构、经济水平、土地利用、人口规模和交通需求等相匹配的轨道交通线网规模，是需要着重关注的问题。

国内外专家在城市轨道交通线网规模分析、预测等方面已经开展了研究，并取得了一定成果。2009年，徐瑞华等[2]以多路径选择为研究条件，对轨道线网上的客流分布建立了分析模型与算法，并最终提出线网合理规模的理论值。2012年，De-Los-Santos等[3]在轨道网络中利用出行时间相关指标评估乘客的鲁棒性，并分析轨道交通网络的合理规模。2015年，卢皓月等[4]将交通、经济和社会等效益进行综合量化分析，进而分析三者效益与线路规模间的关系，建立符合效益最大化的轨道线路合理规模的模型。2016年，孙波成等[5]针对传统轨道网络计算方法的取值难度大、主观性强等缺点，运用 Logit模型，结合规模经济理论，构建综合模型来进行匡算。2016年，陈坚等[6]针对不同预测方法的结果差距较大、操作欠佳等问题，分析城市轨道交通合理规模的影响因素，寻求最优化预测方法，最终得出一种基于改进熵权系数的合理规模计算模型，并以重庆为例进行实证验算。2017年，周玮腾等[7]提出，线网规模的预测通常依赖于客流网络时空分布的预测，将推算城市轨道网络客流时空分布的方法论统称为客流分配理论。

根据以往文献分析可知，相关研究多是基于轨道交通线网物理结构与评价指标对城市轨道线网规模进行分析，而轨道线网规模预测则主要利用单一的预测方法进行研究，且预测方法多为传统、主观的测算模型。当前研究缺乏利用数据学习的客观算法，需要结合多种预测模型进行结果调整，提高模型预测的准确性与科学性。为此，笔者在分析城市轨道线网规模影响因素的基础上，结合BP(back propagation)神经网络模型与交通需求法，对轨道网络合理规模进行预测，从而为城市轨道交通系统整体建设的合理性与科学性提供理论支撑。

2 指标分析

2.1 轨道交通线网规模影响因素

随着我国对公共交通建设的进一步加强与关注，公交都市、TOD发展模式等相继提出与落地，我国城市轨道交通网络系统呈现出复杂网络系统发展的特征，轨道交通的发展也受到政策、经济、城市规模、出行需求等多种因素影响[8-9]。

2.1.1 政策因素

轨道交通规划是城市发展和民生建设的重要内容，也是城市公共交通治理体系和综合架构的组成部分，因此受到政府的宏观政策调控。当前，我国城市轨道交通领域已出台多项有关建设发展的政策，如2003年《国务院办公厅关于加强城市快速轨道交通建设管理的通知》和2018年《关于进一步加强城市轨道交通规划建设管理的意见》等。

2.1.2 经济因素

据研究分析，城市的经济实力与其交通投资规模、居民可接受出行成本成正比关系。轨道交通建设属于昂贵的城市交通建设工程，是大客流城市交通工具，其建设可行性首先会受到城市经济水平的影响。因此，若城市没有一定的经济基础，便无法满足城市轨道交通建设的法规要求。这里选取GDP、第三产业增加值来表征城市社会经济发展水平。

2.1.3 城市规模

选取人口规模及用地规模来刻画城市发展规模。人口规模通常与城市轨道交通的客流量成正比[10]，用地规模也常与公共交通建成里程成正比。轨道交通的规划建设要与城市规模发展相适应，形成相互促进、共同发展的关系，故这里以城市常住人口和建设用地面积来表征城市规模。

2.1.4 出行需求

城市轨道交通的出行需求可在一定程度上映射居民出行选择行为、轨道交通服务水平等，是轨道交通建设及规划布局时需要考虑的重要影响因素，因此选取轨道交通日均客运量来度量其服务水平。

2.2 轨道线网规模影响指标选取

基于以上轨道线网规模影响因素的分析，并考虑近年来轨道建设相关政策的积极态势，选取GDP、第三产业值、人口规模、建设用地规模和日均客运量作为轨道交通线网规模的影响指标。

首先，通过查阅《中国城市建设统计年鉴汇总》《广州市国民经济与社会发展统计公报》等统计资料，准确获取 1999—2018年广州市轨道交通线网长度及各指标实际数据，如表1所示。然后，将从表1所获取的相关数据导入SPSS Statistics V21.0软件中，利用相关性分析功能，计算轨道线网长度和影响指标间变量的相关性，结果如表2所示。

表1 广州市轨道交通线网规模及影响指标数据Table 1 Scale and influence index data of Guangzhou rail transit network

通过表2可以看出，轨道线路长度与5个线网规模影响指标间的相关性系数均大于0.95，且影响指标间的显著性均为 0，表明变量间具有显著的相关性，也反映了选取指标的合理性与有效性。

表2 线路长度及线网规模影响指标间的相关性Table 2 Correlation between line length and network scale impact indices

3 预测模型

由于城市轨道网络规模的发展受到多方面因素的影响，呈现难以解析的非线性关系，所以较难用精准的数学模型去刻画。而 BP神经网络算法具有解决多重因素交叉影响的复杂非线性问题的能力[11]，以及良好的容错和泛化能力，故笔者考虑选取 BP神经网络模型作为轨道线网规模的主要预测方法。此外，为了兼顾传统轨道线网预测方法的优势，选取交通需求法对预测结果进行调整。

3.1 BP神经网络模型

BP神经网络模型的运作思想是基于数据通过反向传播误差值，对模型输入层、隐含层和输出层的权重矩阵进行多次迭代训练，从而达到优化模型的效果。BP神经网络模型基于模型输出值y与目标输出值t之间的均方误差循环调整权值ω，最终使模型的均方误差E最小，计算公式如下：

使用链式法则，计算敏感系数sm，有

式中，ns为迭代次数，m为网络层数。

权值和阈值b的调整公式分别为

式中，α为学习速率。

笔者基于python软件构建BP神经网络模型，基本步骤主要包含数据预处理、网络结构建立、模型参数选取和迭代训练等，步骤流程如图1所示。

图1 BP神经网络模型算法流程Figure 1 BP neural network model algorithm

3.2 交通需求法

交通需求法是一种以满足交通需求为标准进行交通线网规模推算的传统预测方法，具有良好的泛化能力与实际应用经验。可考虑采用该方法对预测结果进行调整，算法计算公式如下：

式中：L为轨道线网规模；Q为交通总量，万人次；α为公交客流比例，%；β为轨道与公交出行的比值，%；λ为轨道交通换乘系数；γ为线网负荷强度，万人次/(km·d)；Q′为轨道交通日客流量，万人次/d。

3.3 基于熵权优化的线网规模预测调整

熵权法是一种基于模型指标的变异程度、结合信息熵概念构建出各模型指标的熵权系数，利用熵权系数调整指标权重，最终确定科学合理的指标权重值[12]，其核心计算公式如下：

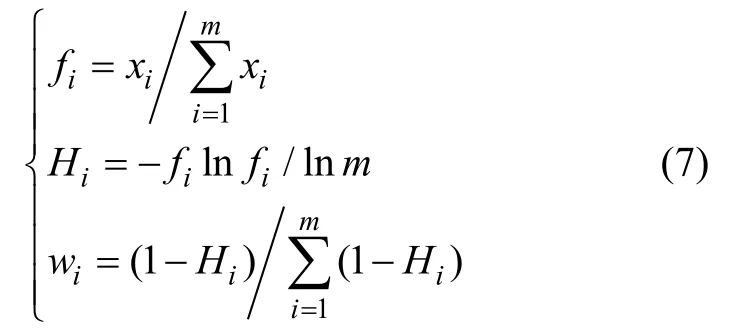
式中，m为线网规模预测模型数量，xi、Hi和wi为第i种模型计算的结果及其熵和熵权。

利用熵权向量，结合交通需求法，对 BP神经网络模型的预测结果进行调整，计算公式如下：

4 案例分析

为量化验证上述构建预测模型的有效性，选取广州市轨道交通线网规模为研究对象，并以近期 2023年的轨道线网规模为预测目标。下面将基于表1的数据，结合基于熵权法的线网规模预测模型进行研究。

4.1 BP神经网络模型预测

为进一步提高 BP神经网络模型的数据处理和拟合计算能力，模型的学习率选为0.01[13]，并利用控制变量法，分别对模型的隐含层数、神经元数、激活函数等参数进行比选确定。

首先，确定模型的隐含层数量。在其他模型参数不变的情况下，设置1和2个隐含层，迭代次数为5 000次，将指标数据输入模型后分别执行10次，获得模型拟合误差均值为0.004 6和0.003 6。因此，模型选取双隐含层结构。

其次，确定各隐含层中的神经元数量。在模型通常采取的神经元个数区间[10，20]中，取10、15、20这3个参数进行模型误差分析。由于输入指标的个数确定为5，则仅需要确定 2个隐含层、隐含层与输出层之间的神经元个数(5，yi，zi)，i=1，2，3。下面基于 3种参数组合进行模型拟合误差值的计算，结果如图2所示。

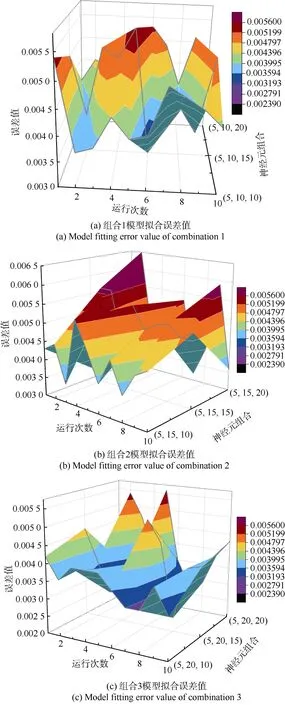
图2 不同神经元组合的模型拟合误差值Figure 2 Model fitting error values of different neurons

从图2中可以看出，以上3组神经元组合的拟合误差值均可达到一定小的误差范围。整体而言，组合2的模型拟合误差值最大，组合3的模型拟合误差值最小。其中，(5，20，10)组合的模型误差最为稳定，且平均误差值最小，故选取此组合作为模型的神经元参数值。

最后，确定模型中神经元的激活函数。不同函数具有不同的收敛速度与饱和性，通常使用的激活函数包含sigmoid、tanh和softmax函数等。同理，分别使用3种传递函数进行模型迭代计算，获得的模型拟合误差均值分别为0.006 5、0.004和0.003 5，故选用表现最优的softmax函数作为模型激活函数。

笔者将广州市 1999—2015年的轨道交通网络长度和GDP、第三产业值、人口规模、建设用地规模、日均客运量的历史数据作为训练集，对构建的 BP神经网络模型进行训练。然后，将2016—2018年的历史数据作为模型的测试集，利用训练后的模型进行计算性能分析，预测结果如图3所示。

从图3中分析得出，所构建的BP神经网络模型预测广州市轨道线网规模的结果与实际值误差较小，进一步表明该模型具有良好的预测性能。

图3 广州市轨道交通线网实际值与预测值Figure 3 Actual and predicted values of Guangzhou rail transit network

基于表1中广州市各指标的历史数据，分别利用指数平滑模型、线性回归模型，计算2023年广州市GDP、第三产业值、人口规模、建设用地规模和日均客运量值，分别为 28 013.5亿元、20 762.2亿元、1 013.6万人、1 553.7 km2、981.4万人次/d。将以上指标数据作为BP神经网络模型的输入值，经过10 000次迭代运行，最终得到2023年广州市轨道线网规模的预测值为735.5 km。

4.2 交通需求法预测

经指数平滑法，计算得到2023年广州市轨道交通的日均客运量约为981.4万人次/d，而预测年轨道交通负荷系数可参照指标相近且轨道交通建设运营时间更长的北京市，取值为1.3，则利用式(6)计算得到2023年广州市轨道线网规模的预测值为754.9 km。

4.3 基于熵权优化的预测结果调整

根据式(7)，分别计算BP神经网络模型和交通需求法预测结果的熵权系数，结果如表3所示。

表3 不同模型预测结果的熵权值Table 3 Entropy weights of different model results

因此，根据熵权优化的轨道线网规模预测模型，计算出 2023年广州市轨道网络规模的预测值为745.2 km，相比《广州市城市轨道交通第三期建设规划(2017—2023年)》中提到的2023年广州市轨道线网总长792 km降低了5.91%。造成这一现象的原因主要有以下两点：广州市轨道交通线网规模计划里程和发展规划仍有调整优化的空间，预测结果可为广州市近期轨道建设和发展提供指导意见；近年来政府积极推进城市轨道交通的供给侧发展建设，导致广州市轨道线网规模的历史数据随时序增长不稳定，而受到模型自身泛化能力和“学习”能力等方面的限制，使得基于数据学习的BP神经网络模型结果存在一定的拟合误差。

5 结语

轨道交通线网规模是城市轨道交通网络规划的核心组成部分，也是影响城市战略布局的重要因素。笔者简要分析了影响轨道网络规模的多种因素，利用相关性分析法，提取了GDP、第三产业值、人口规模、建设用地规模、日均客运量5个模型指标，并结合熵权优化的 BP神经网络模型与交通需求法，构建城市轨道线网规模混合预测模型，最终以广州市为例进行研究分析。具体结论如下：基于 BP神经网络模型和交通需求法，对各模型的预测结果进行标准化，采用信息熵理论，对各模型预测值进行权重分配，兼顾了各计算方法的优势，弥补了单一方法的不足，使得测算结果更加准确有效。

基于熵权法的综合模型预测的合理结果为745.2 km，与广州市2023年轨道交通的实际规划值792 km存在一定的偏差，表明实际规划建设仍可进一步优化调整，并需要更合理的预测方法指导。

本研究量化分析了广州市轨道线网的合理预期规模，基于权值优化整合了两种定量预测模型，可为相关部门的轨道交通规划、设计与决策提供更有效的技术支撑，有利于更加精准地从供给侧提供轨道交通服务。