超超临界汽轮机可倾瓦轴承改造的研究与应用

鲁豫鑫，汤 昀，何新友

(1.上海电气电站设备有限公司汽轮机厂，上海 200240；2.浙江浙能嘉华发电有限公司，嘉兴 314000)

但在汽轮机机组的实际运行中，由于转子经常会受到某些外力或外因(如汽流力、基础非均匀性沉降、长期运行后的动静磨损等)的干扰，同时汽轮机1号轴承仅支承高压转子一半的载荷，比压较低，且为椭圆瓦形式，无法快速有效地抑制振动，因此1号轴承的相对振动偏大。

本文基于滑动轴承流体动力润滑理论，对椭圆轴承和可倾瓦轴承进行建模和求解，从轴承功耗、最小油膜厚度、润滑油需油量、刚度系数、阻尼系数等多方面进行了对比分析，并通过某超超临界汽轮机机组的现场改造试验结果，验证了可倾瓦轴承降低机组振动的效果，为今后电厂解决同类问题提供参考。

1 椭圆轴承与可倾瓦轴承对比

1.1 结构介绍

椭圆轴承和可倾瓦轴承的常见结构和油膜示意如图1所示[1]，模型如图2所示。从结构上看，椭圆轴承由上、下两半瓦组成，每半瓦各有1个收敛的楔形间隙，单个轴承最多可以形成两个动压油膜。而可倾瓦轴承得益于瓦块可以摆动的特性，在每个瓦块上都可以单独形成1个收敛的楔形间隙，即每块瓦形成1个油膜[1]。在转子受到外部扰动时，与扰动方向相反的油膜力就会增大，这可对扰动产生抑制作用，从而减小振动值。

(a)椭圆轴承 (b)可倾瓦轴承

(a)椭圆轴承 (b)可倾瓦轴承

1.2 设计参数对比

考虑到改造前机组原椭圆轴承的比压较低，对稳定性不利[2]，更改为可倾瓦轴承时，将轴承宽度减小，以提高轴承比压。且可倾瓦轴承靠瓦背面的垫块自定位，因此将轴承底部的球面垫块更改为圆柱面垫块。

超超临界汽轮机1号轴承所使用的椭圆瓦和拟改造的可倾瓦轴承参数如表1所示。

表1 椭圆轴承和可倾瓦轴承结构参数及说明

1.3 动静特性计算对比

基于流体动力润滑理论，将反映润滑油黏度随温度变化的温黏方程(1)引入传统的Reynolds方程(2)中，计入温度对润滑油黏度的影响，并结合能量方程(3)以考虑轴承油膜的温度分布，建立径向动压滑动轴承的理论分析模型。

μ=μ0e-α(t-t0)

（3）将“套路”与新思路有效结合，实现解题效率的最大化。还有些情况下单一应用“套路”或构建新思路都难见成效，我们可以尝试将它们“融为一炉”。

(1)

式中：μ为润滑油的黏度；t为润滑油的温度；t0为润滑油基准温度；μ0为润滑油基准温度下的黏度；α为温黏指数。

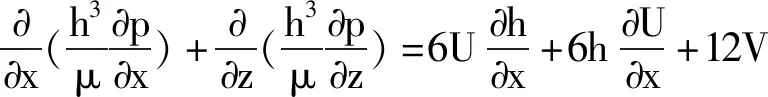
(2)

式中：x为沿轴颈圆周方向的坐标；z为沿轴向的坐标；h为径向油膜厚度；p为油膜压力；U、V分别为轴颈上某点对轴瓦上对应点的相对速度的切向分量和径向分量。

(3)

式中：ρ为润滑油密度；cv为润滑油的比热容。

利用有限差分法对上述模型进行迭代求解，可以获得轴承的油膜压力和温度分布，再通过积分可求得轴承功耗、润滑油流量等参数，并利用微小扰动法[3]求得轴承刚度阻尼系数等动静特性参数，计算流程如图3所示。

图3 计算流程图

2种轴承在3 000 r/min的转速下，最小油膜厚度和最高油膜温度计算结果如表2所示。可以看出，更换可倾瓦轴承后，虽然轴承宽度减小导致了比压增大，但由于可倾瓦轴承的设计间隙比较大，预负荷较小，计算得出的轴承最小油膜厚度有所增大，所以最高油膜温度基本与改造前的椭圆轴承相同。

表2 椭圆轴承和可倾瓦轴承油膜参数

2种轴承的功耗和润滑油量对比分别如图4和图5所示。可以看出，更换轴承形式后，功耗和需油量均有所下降。在3 000 r/min的转速下正常运行时，功耗较原轴承降低23.8%，润滑油需油量降低24.7%。功耗降低可以提升汽轮机效率，而需油量减小表示更换轴承时无需对润滑油系统进行重大变更。

图4 椭圆轴承和可倾瓦轴承功耗随转速变化曲线

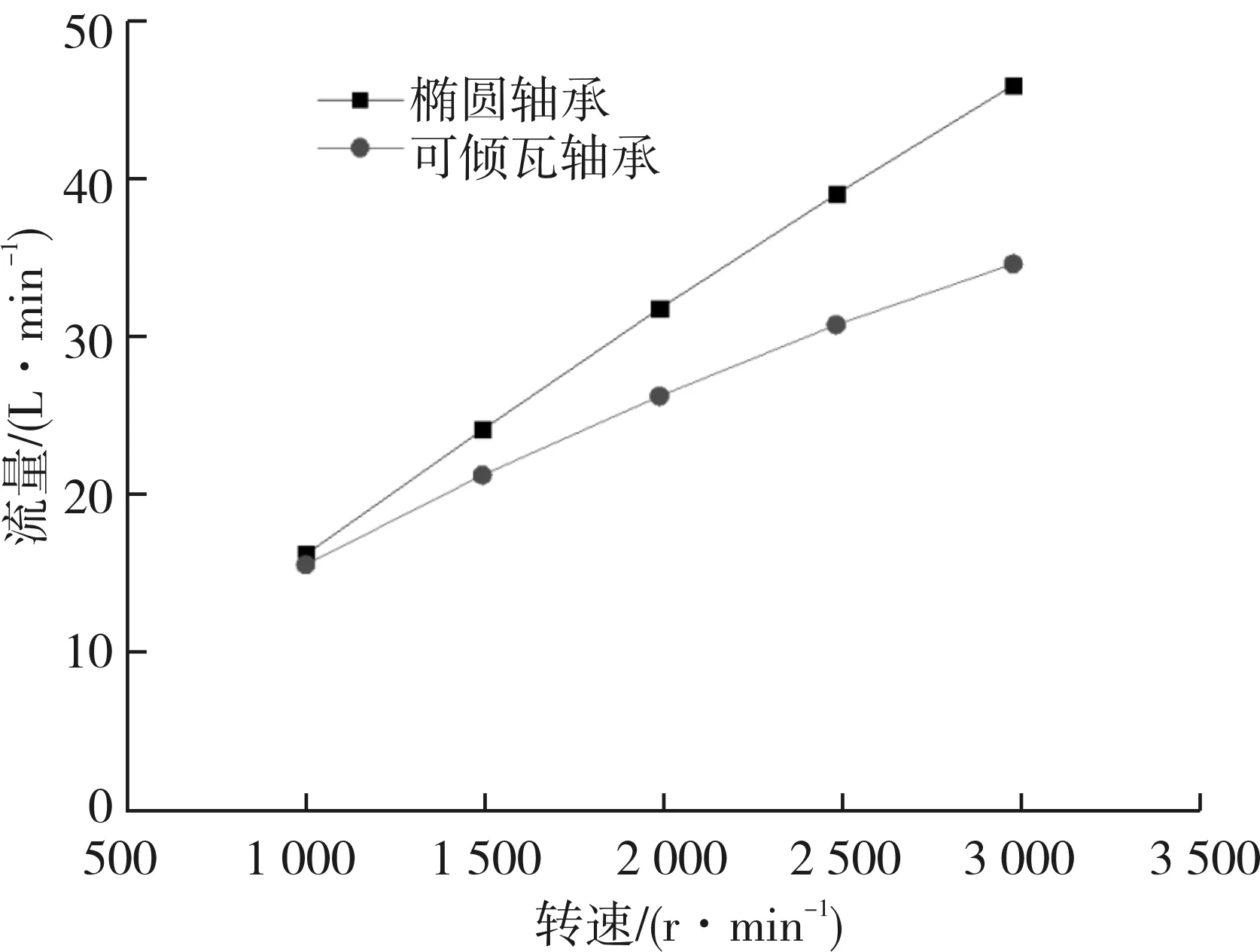
图5 椭圆轴承和可倾瓦轴承润滑油量随转速变化曲线

对轴承稳定性的判定需要用到油膜的8个动力特性系数[4]：4个刚度系数k表示油膜力对轴心位移的影响；4个阻尼系数b表示油膜力对轴心变位速度的影响。

2种轴承的刚度系数计算结果对比如图6和图7所示。可以看出，椭圆轴承竖直方向刚度较大，水平方向刚度很小，而可倾瓦轴承得益于可以形成多个油膜的结构，其水平刚度和竖直刚度系数相等，相比于椭圆轴承，竖直刚度虽减小了20%～27%，但水平刚度提高了4.5～5.7倍。在交叉刚度方面，椭圆轴承的交叉刚度随转速增大而减小，直至负值，而可倾瓦轴承的交叉刚度一直保持在0左右，即轴承的交叉刚度不会促进转子涡动，故稳定性极佳[4]。

图6 椭圆轴承和可倾瓦轴承主刚度系数随转速变化曲线

图7 椭圆轴承和可倾瓦轴承交叉刚度系数随转速变化曲线

2种轴承的阻尼系数计算结果对比如图8和图9所示。同样可以看出，椭圆轴承竖直方向阻尼较大，水平方向阻尼较小，而可倾瓦轴承得益于可以形成多个油膜的结构，其2个方向的阻尼系数相等，相比于椭圆轴承，竖直方向阻尼系数减小了44%～47%，但水平方向阻尼系数提高了2.5～5.3倍。在交叉阻尼方面，椭圆轴承的交叉阻尼随转速增大而迅速减小，而可倾瓦轴承的交叉阻尼一直保持在0左右，即转子水平或竖直方向的轴心扰动不会对另一方向产生影响。

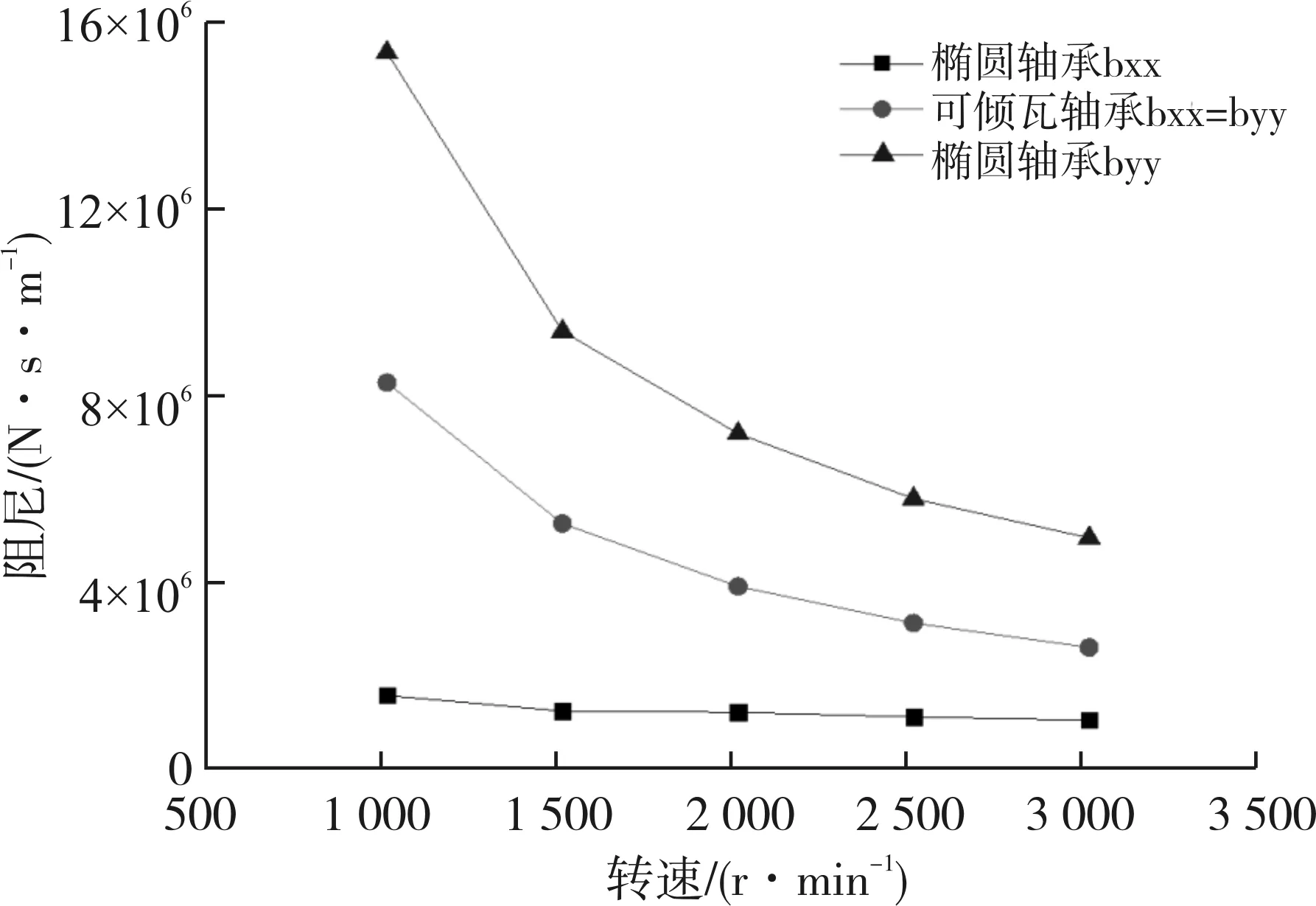
图8 椭圆轴承和可倾瓦轴承主阻尼系数随转速变化曲线

图9 椭圆轴承和可倾瓦轴承交叉阻尼系数随转速变化曲线

将轴承的刚度阻尼系数代入转子系统的运动微分方程(4)[5]中，可以求解得到系统的运动特性，进而可以得到判定系统稳定性裕度的参数，即对数衰减率，公式如式(5)所示。

(4)

式中：q为系统的广义位移；M、B、K为系统的质量、阻尼和刚度矩阵；F为作用在系统上的广义外力。

(5)

式中：δ为对数衰减率；qi、qi+1为相邻2次振动的最大位移。

对数衰减率表征为在受到外界干扰后，相邻2个振动周期的振幅比值的对数[5]。椭圆轴承和可倾瓦轴承在转子系统中的对数衰减率如表3所示。可以看出，采用可倾瓦轴承后，对数衰减率增大了13.7%，对振动的抑制作用增强。

表3 椭圆轴承和可倾瓦轴承的对数衰减率

2 实际应用

根据理论计算结果，对该超超临界汽轮机组进行了实际改造。

改造前后的现场试验振动数据分别如图10和图11所示。可以看出，改造前的1号轴承最大相对振动已超过传感器量程250 μm，平均值为92.99 μm；改造后振动的最大值为99.1 μm，平均值为52.04 μm。相对振动的平均值降低了44%。

图10 改造前机组振动曲线

图11 改造后机组振动曲线

3 结 论

本文基于滑动轴承的流体动力润滑理论，对可倾瓦轴承和椭圆轴承进行了多方面的对比分析，重点关注其动静态特性。根据工程的实际应用效果得出了以下结论：

1)相对于椭圆轴承，可倾瓦轴承拥有更好的稳定性和抑振性，将其用于超超临界汽轮机的1号轴承，可以有效降低振动，提高机组的安全性；

2)超超临界汽轮机组的1号轴承更改为可倾瓦形式后，流量和功耗相对减少，无需更改润滑油系统的设备。