燃气轮机透平叶片的外表面传热特性分析

崔耀欣，赵锦杰，何 磊

(上海电气燃气轮机有限公司，上海 200240)

为了提高燃气轮机的性能和做功能力，降低燃料消耗，提高燃气轮机热效率，透平前平均温度从20世纪50年代的1 100 K发展到今天接近1 900 K。为保证热部件在高温燃气环境下仍然可以安全可靠地运行，必须对透平叶片采取复杂的冷却方式[1]。为了提高冷却设计的准确性，必须对燃气与叶片表面之间的换热情况进行更为精准的分析。

朱彦伟等[2]结合试验和数值模拟，对叶片的外换热进行了影响因素分析，研究结果显示马赫数是影响外换热的最主要因素。何磊等[3]、Chen等[4]采用商业软件CFX对表面粗糙度对气动性能的影响进行了分析，发现表面粗糙度的增大会造成压气机的效率和压比一定程度的降低，这与Bogard等[5]的发现类似；Blair[6-8]试验研究了湍流度从0.25%到7%对平板外侧传热系数的影响，结果表明湍流度最大增加约20%；Ames[9]对带内部冷却结构、无气膜的空心的C3X叶片进行了系统的表面传热系数的影响研究，针对影响它的各种因素进行对比分析，得到了可供参考的数据库。

随着现代CFD技术的不断发展，数值模拟已经从传统的二维计算软件STAN5发展到含有各类湍流模型和修正模型的CFX和Fluent等软件[10-11]，这些软件对流动中有附面层流动、角涡、马蹄涡和二次流等各类现象的预测更加准确。目前对三维叶片结构的传热系数的准确预测得到了不少工程应用，它的优势是可以得到比传统的二维计算更详细的传热系数分布情况，并且对端壁的换热也有较好的预测效果[12]。

本文在前述对于叶片外换热研究的基础上使用数值模拟软件对温差、湍流度和端壁等影响外换热的因素进行了详细的研究，总结了其对外换热特性的影响规律，旨在为透平叶片表面传热系数的研究提供一定参考。

1 数值方法

1.1 几何模型和网格划分

几何模型采用燃气轮机透平叶栅几何模型。为了避免回流现象影响计算收敛，叶栅通道进出口均延长了一定长度。具体的几何模型见图1。

图1 叶栅通道的几何模型

计算网格采用结构化网格，对叶片外表面进行边界层加密处理。近壁面第1个网格单元中心的近壁面距离满足壁面函数律的条件，所采用的网格已通过无关性验证。该叶栅模型网格见图2，节点总数为424 250，单元总数为443 750。网格质量良好。

图2 叶栅通道的六面体网格

1.2 数值计算方法

本文的数值模拟不仅包含主流大部分区域的湍流状态，也对叶片表面附近的层流及其分离的流动状态进行了设计，所以采用工程中广泛应用的雷诺平均数值模拟(RANS)方法[13-14]，选取多个不同的湍流模型。其中对于k-ω湍流模型及SST湍流模型而言，需要保证第1层网格节点y^+在1左右。表1给出了研究过程中选取的各个湍流模型。

表1 CFX中选取的湍流模型

壁面黏性阻力系数的定义为:

(1)

式中：τw表示壁面切应力，在数值计算结果后处理中为沿着流向的切应力。壁面局部努赛尔特数的计算公式为：

(2)

壁面传热系数的计算公式为：

(3)

(4)

式中：Tw为叶片壁面温度，Tb为气体温度，H为传热系数，λ为金属导热系数，Tf为定性温度(确定物性参数)，工程应用上Tb、Tf一般取进口温度。

图3给出了CFX在不同湍流模型下的传热系数分布。结合表交典型的MarkⅡ型叶片和C3X叶片表面的传热分布特征[15]，压力面边界层由前缘处向后逐渐增厚至一定厚度后，会发生边界层分离。而吸力面上的边界层流动变化比压力面明显，从前缘开始，随着层流边界层的发展，其厚度逐渐加大，传热系数逐渐减小；进入转捩区域，边界层内的扰动加大，换热加强，即传热系数逐渐增大；当转捩结束，进入完全湍流阶段后，湍流边界层沿流向发展，厚度逐渐增大，从而导致换热减小。因此，从传热系数的变化过程可以判断转捩过程的起始及结束。从图3中可以看出，k-ω湍流模型对这种边界层的变化捕捉显示不够明显，而SST、一方程转捩模型和二方程转捩模型都能捕捉到这种变化趋势。

图3 不同湍流模型下的中径处壁面传热系数分布

一般情况下认为壁面黏性阻力系数最小值为转捩起始点，紧接着的极大峰值点为转捩结束点。因此对壁面黏性阻力系数的捕捉也是判断转捩过程的一种方法。图4给出了CFX不同湍流模型下的壁面黏性阻力系数分布。从图4中可以看出SST湍流模型和SST一方程湍流模型基本能捕捉到转捩过程，且其结果符合叶片黏性阻力系数分布的一般规律。

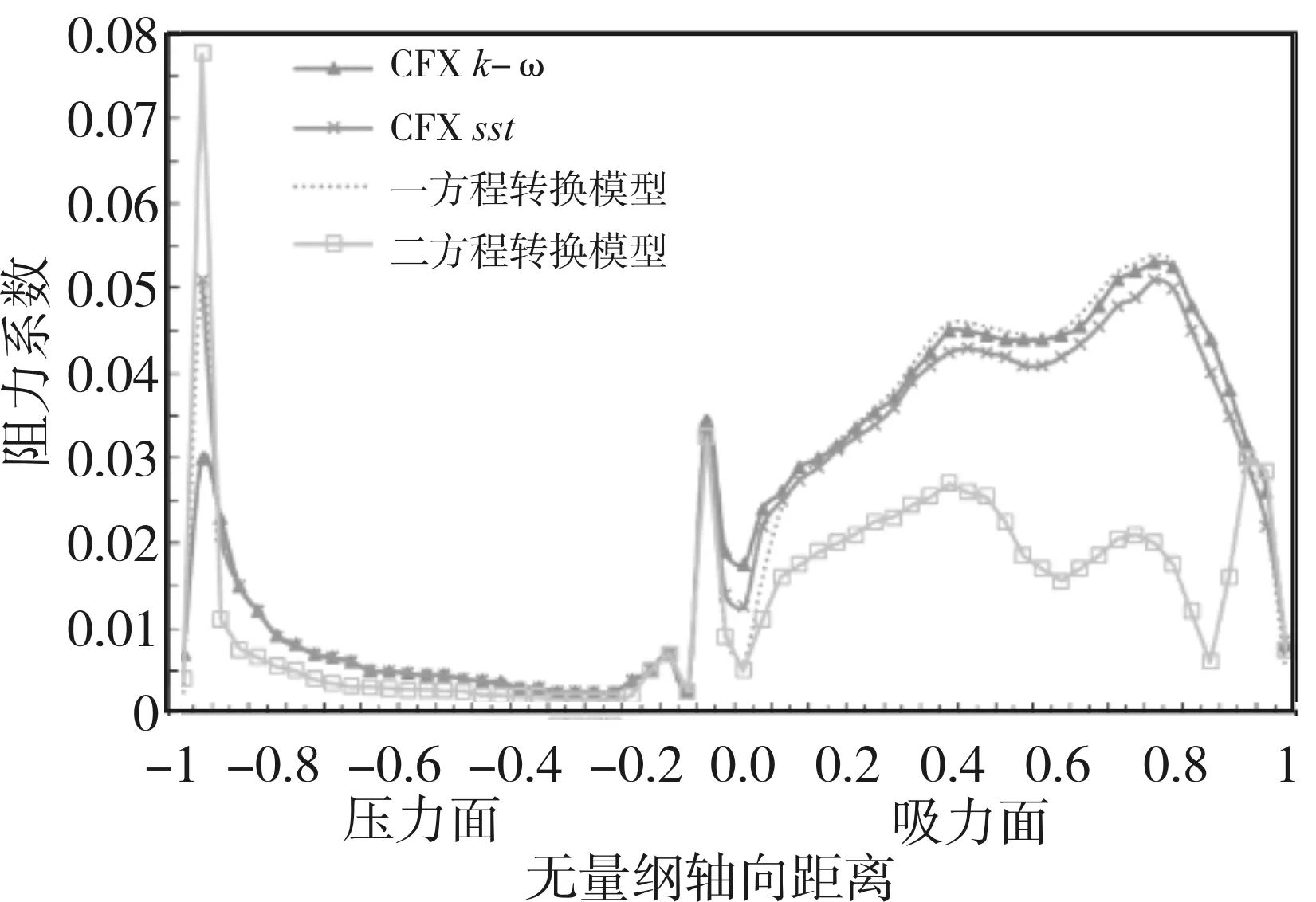
图4 不同湍流模型下的中径处壁面黏性阻力系数分布

2 计算结果及分析

2.1 温差对表面换热的影响

由于叶片表面跟主流存在着一定的温差，为了了解温差对叶片表面传热系数分布的影响，保持主流温度不变，研究了Tw/Tg(Tg为主流温度)为0.68、0.78、0.88和0.98四种工况对表面换热的影响。图5给出了叶片不同Tw/Tg下中径处壁面传热系数分布。从图5中可以看出在绝大部分层流区(即转捩未开始阶段)，Tw/Tg对表面换热的影响基本可以忽略，但在湍流区，总体换热水平随着Tw/Tg的增大而减小，这与上文提到的NASA报告[9]基本一致。从图5中可以看出Tw/Tg=0.98时的传热系数相对于其他3条曲线明显偏低。由于Tw/Tg过大会导致叶片和主流的温差过小，这样的计算结果会导致误差增大，因此本文建议后续叶片计算主要采用的Tw/Tg范围为0.7～0.8。

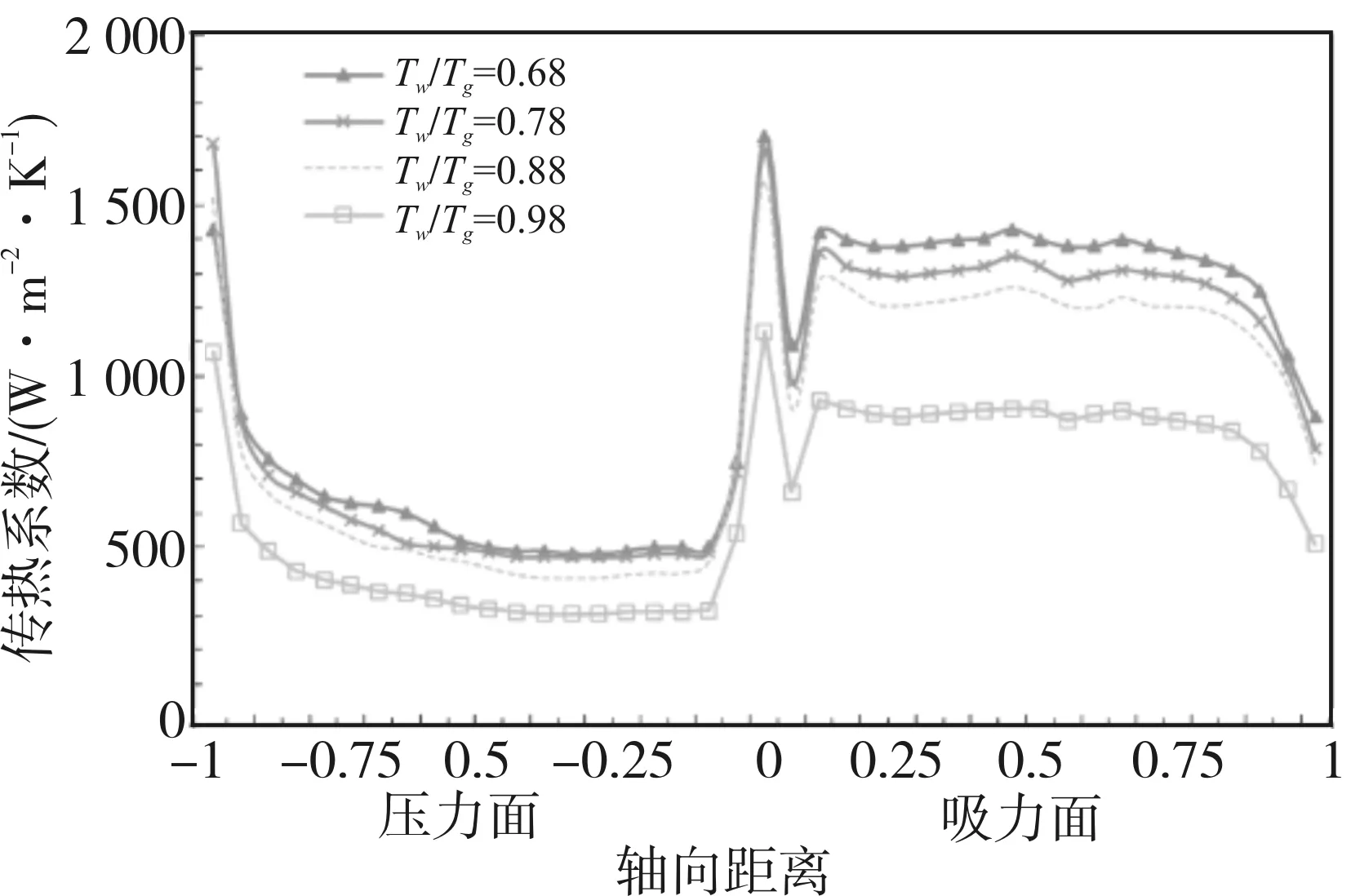
图5 SST湍流模型中径处壁面传热系数分布

2.2 湍流强度对换热的影响

为了研究湍流度对叶片表面换热的影响，数值计算选用了SST湍流模型，结合Goebel等[16]对比较接近实际工作条件的燃烧室出口湍流强度进行的实验研究，选取进口湍流度分别为6%、10%和20%进行数值模拟。

图6和图7给出了湍流度为6%时叶片表面的热流密度分布。从图6中可以看出叶片表面的热流密度变化比较剧烈，前缘驻点附近区域热流密度最高，驻点以后由于层流边界层作用，热流密度逐渐减少，到转捩点后，层流转变为湍流，热流密度开始剧增。从图6中也可以看出吸力面平均热流密度比压力面大，主要原因是由于通道涡和前缘马蹄涡压力面分支组成的二次流到达吸力面，具有较高的湍流强度，以致换热增强。热流密度间接反映了叶片表面传热系数的分布，图8和图9给出了叶片表面的传热系数分布。传热系数分布与热流密度分布规律类似。

图6 压力面热流密度分布

图7 吸力面热流密度分布

图8 压力面传热系数分布

图9 吸力面传热系数分布

图10给出了不同湍流度对叶片中径处传热系数分布的影响。从图10中可以观测到前缘附近的传热系数最高，从前缘到尾缘，传热系数首先逐渐降低，然后又逐渐升高，这与附面层转捩位置有关，吸力面的平均传热系数比压力面大。同时，从图10中可以看出湍流度对叶片表面传热系数的影响比较小，只在吸力面距离前缘0.2附近有些变化。较大的湍流度有较大的传热系数。

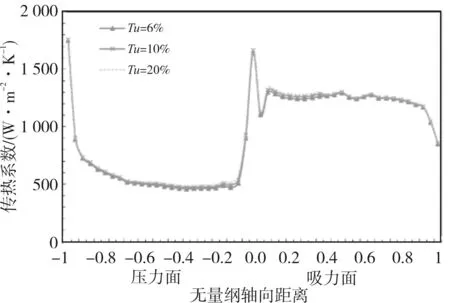
图10 SST模型叶片中径处的表面传热系数分布

2.3 端壁对换热的影响

流体通过直立在平板上的圆柱体时，其端壁边界层卷起成涡，流体经过圆柱体两侧形成类似马蹄形的流线，简称马蹄涡，压力侧马蹄涡分支会演变成通道涡，并向吸力面侧马蹄涡分支靠近。York等[17]指出端壁问题的基本特性是多样及复杂变化的，吸力面侧马蹄涡分支围着通道涡盘绕，而不是黏附在吸力面上。旋涡还把入口边界层气流带向叶片的顶部。这些复杂的二次流分布可能造成沿端壁横向的传热特性变化剧烈。

图11给出了透平叶片端壁的静压系数分布云图。从图11中可以看出主流的压力分布均匀，通过叶栅通道后会形成从压力面到吸力面方向的强大压力梯度。从图11中可以辨别出端壁通道涡路径方向。

图11 叶片端壁上的静压系数分布

叶片端壁上的传热系数分布如图12所示。由于前缘马蹄涡的存在，马蹄涡的卷吸作用强化了前缘附近端壁的换热，靠近叶片区域吸力面侧传热系数较高，压力面侧的高温气体被马蹄涡卷至下一叶片的吸力面。从传热系数梯度的突变区域可以看出旋涡的路径，传热系数从压力面到吸力面逐渐递增。端壁上的最低传热值发生在压力面附近，传热系数低值区域呈弧形从鞍点区域延伸到压力面，又从压力面进到后缘附近的通道内。从图12中可以看出叶片尾流区域是传热最强的区域。在叶片尾缘部分，通道内的压力梯度会引起气流在压力面上向下流动、吸力面上向上流动，叶片尾缘区域的主流气体被此压力梯度影响，高换热区域在叶片尾缘部分也呈现由压力面向吸力面流动的趋势。

图12 叶片端壁上的传热系数分布云图

图13给出了叶片吸力面和压力面的传热系数的详细分布情况。从分布图中可以看出，压力面上传热分布呈现很好的二维性。因为压力面侧旋涡引起的大尺度影响非常小，所以通道涡向吸力面的移动对压力面影响不大。而其在吸力面上的径向影响与Goldstein等[18]发现的规律类似，在轴向距离0.3左右，吸力面分支旋涡被推离端壁并沿着吸力面移向通道涡的上方，引起传热分支在叶高方向的强烈变化。当旋涡顺着叶片吸力面上移，并被通道涡带至下游时，当地的传热系数达到峰值。叶片吸力面尾缘部分传热系数三维分布如图 14所示，图中给出了其最大值的位置。

(a)压力面

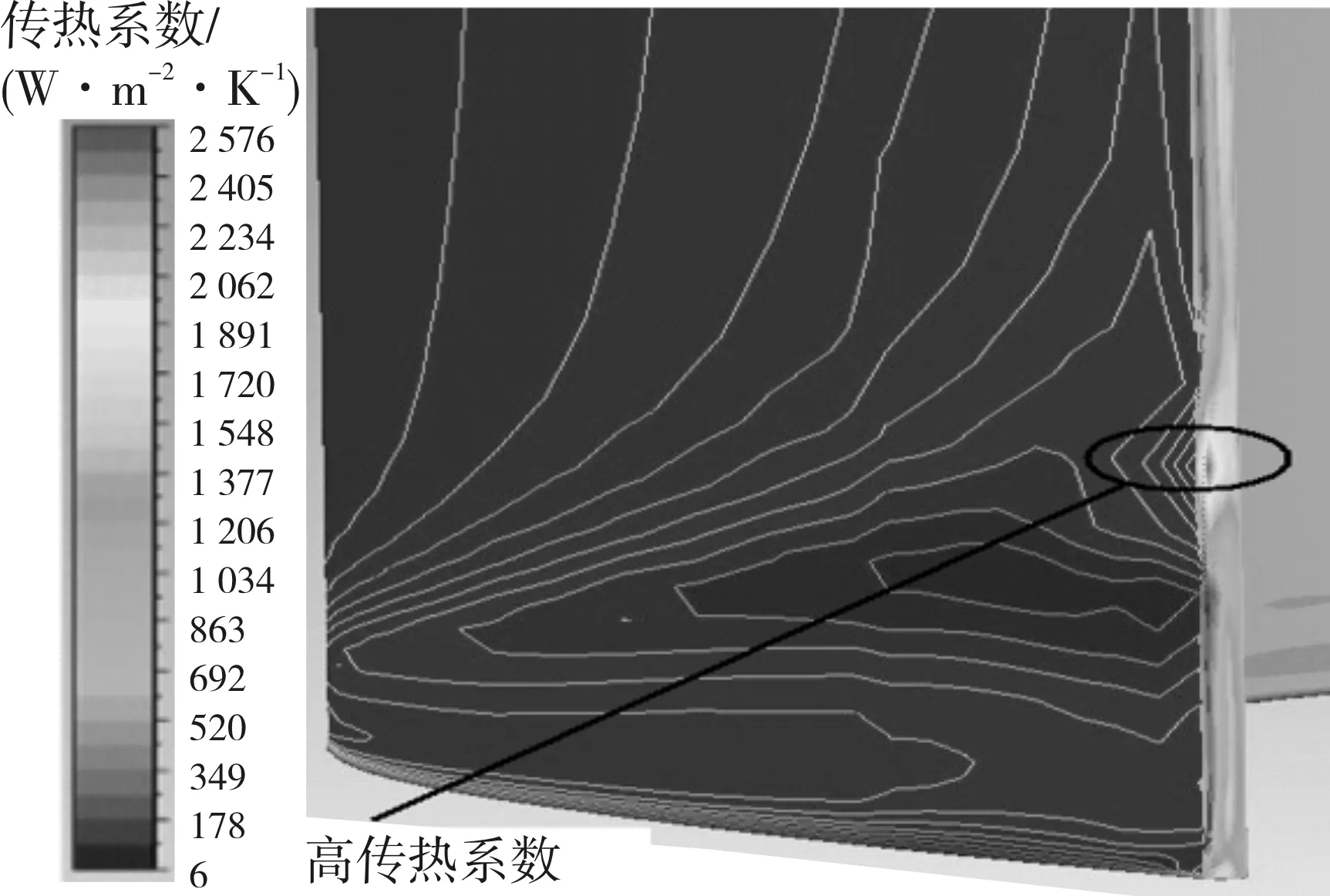
图14 叶片吸力面尾缘部分传热系数三维分布

3 结 论

本文针对叶片表面换热问题，通过采用数值模拟的方法，研究了温差、湍流强度和端壁的影响，得出如下结论：

1)叶片表面与主流的温差对叶片表面的换热分布影响较小，仅在吸力面的湍流区对传热系数有些许影响。通过比较不同的壁面温度计算结果，发现本文壁面温差较小的结果与其他文献的计算结果偏差较大，因此计算过程中温差不能取得过小(建议温度比Tw/Tg的范围为0.7～0.8)，否则会导致计算误差增大。

2)叶片外表面传热系数受湍流度的影响不大；叶片表面的传热系数变化比较剧烈，前缘驻点附近区域换热最剧烈，驻点以后由于层流边界层作用，换热逐渐减弱，到转捩点后，层流转变为湍流，换热开始剧增；吸力面平均传热系数比压力面大，在叶片设计过程中需要针对前缘滞止点和吸力面后缘外传热系数较大的地方(0.8～1处)进行冷却。

3)由于前缘边界层引起的马蹄涡卷吸作用，叶片端壁前缘区、吸力面及叶片尾流区的换热强度较大；叶片压力面传热分布呈现出很好的二维性；在吸力面0.3轴向距离附近，表面开始受马蹄涡的影响，换热分布呈现三维特性；通道涡从压力面向吸力面移动，并顺着吸力面上移，最大换热值出现在叶片尾缘近端壁处。