基于小波变换和残差神经网络模型的轴承故障诊断

杨腾，宁芊，陈炳才

（1.四川大学电子信息学院，成都610065；2.大连理工大学计算机科学与技术学院，大连116024）

0 引言

大型机电设备是复杂的非线性动态系统，具有不确定性、非线性、时变等特点，故障状态复杂，干扰因素多[1]。滚动轴承作为机电设备的重要组成部分，故障如若发现排查不及时，或是诊断出错往往会导致生产延误和维修费用过多，甚至成为生产作业人员人身安全的重大隐患[2]，因此准确及时的检查与诊断滚动轴承的故障以最大限度地降低性能下降和避免危险的发生是必要的，也是故障诊断研究者们近年来不断追求的。

早期故障诊断一般先对收集到的滚动轴承振动信号进行分析处理，选取合适的特征信号进行提取[3]，然后再输入到支持向量机（SVM）、模糊C均值聚类等机器学习算法中进行故障诊断和分类。传统的特征特征提取可分为三类：基于时域分析的信号特征提取，基于频域分析的信号特征提取以及基于时频分析的信号特征提取[4]。Yan提出的一种多域特征支持向量机优化分类算法在滚动轴承故障诊断中的应用[5]，从时域、频域、时频域等多域方面提取故障特征信息然后利用基于粒子群优化的支持向量机分类模型，实现了滚动轴承多故障状态的识别。Li提出了一种基于置换熵、集成经验模式分解和支持向量机优化的轴承故障诊断模型[6]，通过整体经验模态分解（EEMD）将振动信号分解为一组固有模态函数，利用特征空间中簇间距离（ICD）优化的SVM对故障类型和故障严重程度进行分类。然而基于特征提取的信号处理技术比较依赖人为的特征选取和先验知识，在一些时候可能遗漏原始故障特征，而且泛化性能较低使人们开始寻找新的方向[7]。

随着深度学习热潮的兴起，其在自然语言处理、图像识别等领域的广泛应用也给轴承故障诊断研究者们带来了新的方向。深度学习从收集的信号中自动的提取有用特征而不再依赖人工特征提取，使用端到端的形式将原始信号数据和深度学习网络相连实现对滚动轴承故障的诊断分类[8]。近年来，较为公众熟悉的深度学习基本模型框架包括深度置信网络（DBN）、卷积神经网络（CNN）、堆叠自动编码机（SAE）、递归神经网络（RNN）[9]。Xu提出了一种新的自适应快速深卷积神经网络能从振动信号中自动学习复杂有用的特征，利用指数线性单元激活函数和全局平均池构造了深度卷积神经网络结构，具有广阔的接受域[10]。Wu提出一种用于轴承故障诊断的自适应深度转移学习方法，使用基于实例转移学习的长短时记忆递归神经网络（LSTM）模型，生成辅助数据集，引入GWO（Grey Wolf Optimization）优化算法，自适应地学习联合分布自适应的关键参数，其模型在标记故障数据不足的情况下依然具备很好的有效性和鲁棒性[11]。ZHANG提出一种基于改进的卷积神经网络的轴承故障诊断方法，将一维原始数据转换为二维图像数据，通过CNN神经网络消除专家经验对特征提取的影响自动的提取特征并对故障进行诊断[12]。以上所构建的神经网络多是对滚动轴承信号单一域上的诊断，不能很好的学习到其他域的特征，所以其泛化性和准确性依然存在提升空间。

为了解决以上问题，本文提出一种基于小波变换和残差神经网络模型的变负载轴承故障诊断模型。该模型将采集到的振动信号通过小波变换将一维时域信号映射到二维时频域中，将得到的二维时频信号进一步压缩后作为改进残差网络的输入，由网络自身对信号进行特征提取并进行诊断。

1 小波变换

小波变换由法国学者Morlet于提出，传统的快速傅里叶变换将时域信号变换到频域上，能直观的从频域上对信号进行分析，但是无法得知信号在不同时间点上的频率信息，小波变换使用面积固定而形状可变的窗函数通过多辨率分析能很好的平衡时间分辨率和频率分辨率。连续小波变换公式（1）如下：

其中w(a,b)为小波变换系数，φ(t)ϵL2(R)为基本小波或母小波，其傅里叶变换∅(w)满足条件（2）：

对母小波进行伸缩、平移将得到一系列小波函数：

2 实验数据处理

2.1 轴承原始数据处理

凯西西储大学（CWRU）滚动轴承数据中心的数据被广泛应用于滚动轴承诊断领域和信号分析领域，大量论文期刊也以此作为训练数据，为避免数据非同一分布带来的实验误差，本文所有数据均使用CWRU数据集。驱动端轴承故障由电火花在内圈、外圈、滚动体三个位置点触加工形成：内圈损伤、外圈损伤、滚动体损伤三种故障位置类型，故障位置损伤有三种不同损伤尺寸分别为：0.007inch、0.014inch、0.021inch，共计九种故障类别，加上滚动轴承正常工作状态共计十种轴承状态标签。

在模拟实验中使用型号SKF-6205的驱动端作为实验对象，信号采样频率为12KHz。根据轴承工况的不同，数据集共四种分别为：0hp、1hp、2hp、3hp。每个样本由2048个振动点表征（使用随机抽取的方式从长度为10万左右的振动点序列中随机的抽取一段连续的长度为2048的振动点，若重复抽取则舍弃重新抽取）。图1是1hp工况下轴承不同状态标签下的样本时域波形图。鉴于篇幅限制仅展示正常状态以及损伤尺寸0.007inch的三种故障状态。

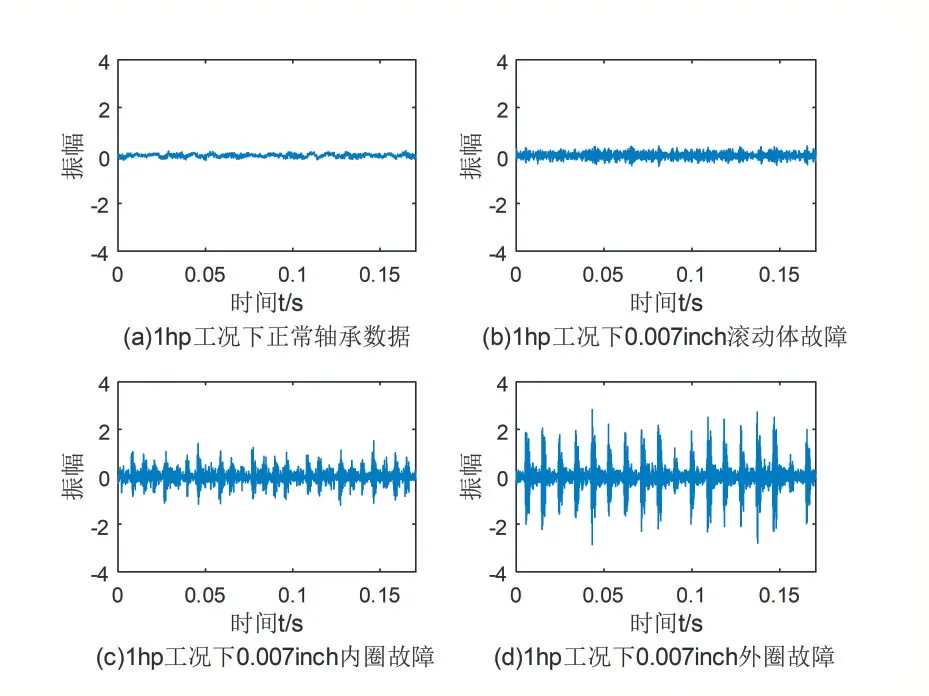
图1 不同故障类型样本的时域波形图

图2是时域样本经过小波变换后得到的时频图，其中采样频率12K，尺寸序列长度为256，使用小波名为cmor3-3。从图中我们能够直观的看到不同故障状态的能量分布具有良好的分辨性，其中轴承正常状态下的能量集中在低频分段且在整个时间轴上波动较小，故障状态下则集中在高频分段并且在时间轴上出现明显波动对比明显。小波变换后的时频图展示出良好的时间分辨率和频率分辨率。

图2 不同故障类型样本的小波变换时频图

由于小波变换直接输出的时频图维度较大，若直接将其作为网络模型输入计算量巨大，所以我们将其维度压缩至128×128，使深度神经网络能够更快的训练模型，更快的诊断故障，提高模型实际应用的实时性。图3为压缩后的小波变换时频图，从图中可以看到对比压缩前的时频图压缩后的时频图特征基本保留完整，未出现明显的特征丢失。

图3 不同故障类型样本的小波变换时频压缩图

2.2 轴承原始数据处理

每种工况下滚动轴承有正常状态、内圈故障状态、外圈故障状态、滚动体故障状态，除正常状态外其余三种状态均有上述提及损伤尺寸共十种轴承状态。每种轴承状态使用800个样本作为训练集200个样本作为验证集。单一工况数据集信息如表1所示。

表1 单一工况下的数据集

为验证本文模型在不同工况下的适应性，设置0hp、1hp、2hp、3hp四种变负载数据集，并使用不同负载数据集进行交叉验证。数据集设置可见表2。

表2 交叉验证数据集

3 相关模型介绍

3.1 残差网络

众所周知，在深度神经网络中网络的深度是至关重要的，为追求更高的精确度研究者们往往会选择扩大训练集样本或是更深的网络结构，然而选择更深的网络结构同时带来的两个问题：梯度消失/梯度爆炸以及网络的退化问题。前者可以通过归一化初始化、中间归一化层得到解决，但是对于后者研究者们发现对一个网络逐渐增加其的深度，模型的准确度逐渐达到饱和然后迅速退化。

为解决模型网络层数过深而导致的退化问题，K.He等人受传统深度卷积神经网络（VGGNET）的启发于2017年提出了残差网络（ResNet）[13]。VGGNET使用多个卷积核尺寸为3×3的卷积层堆叠构成卷积组，代替传统的大卷积核卷积层，有效的减少了参数，加快了网络的学习速度。ResNet在VGGNET的基础上采用一种“shortcut connections”链接方式如图4，假设将一组堆叠的神经网络层的映射近似为恒等映射，即该组神经网络层的输入为X，堆叠的非线性层映射为F（X），其输出H（X）则表示为：H（X）=F（X）+X，当H（X）近似为X时，这组堆叠的网络层可看做一个恒等映射，F（X）则被看做一个残差函数有：F（X）=H（X）-X，因此在神经网络中添加若干恒等映射既加深了网络深度也不会导致网络的退化。故模型仅需最小化F（X）将化残差函数逼近于0即可解决网络过深带来的性能退化问题。

图4 快捷连接

恒等残差块如图5（a）所示其输入的激活和输出的激活具有相同维度，由三个二维卷积核组成，三个卷积核紧连着BatchNorm对数据进行归一化处理，最后一个卷积层和前两个卷积层的不同点在于其没有在BatchNorm归一化后直接联接修正线性单元ReLU激活函数，而是和恒等残差块的输入通过shortcut connections进行整合再使用RuLU进行激活。

随着网络结构的深入激活函数输出的feature map的维度逐渐增大，当输入输出的维度不一致时恒等残差块不再适用，于是使用图5（b）所示的卷积残差块结构。卷积残差块在shortcut connections添加一个卷积核和BatchNorm归一化将输出和输入对齐到相同维度再使用RuLU进行激活处理。

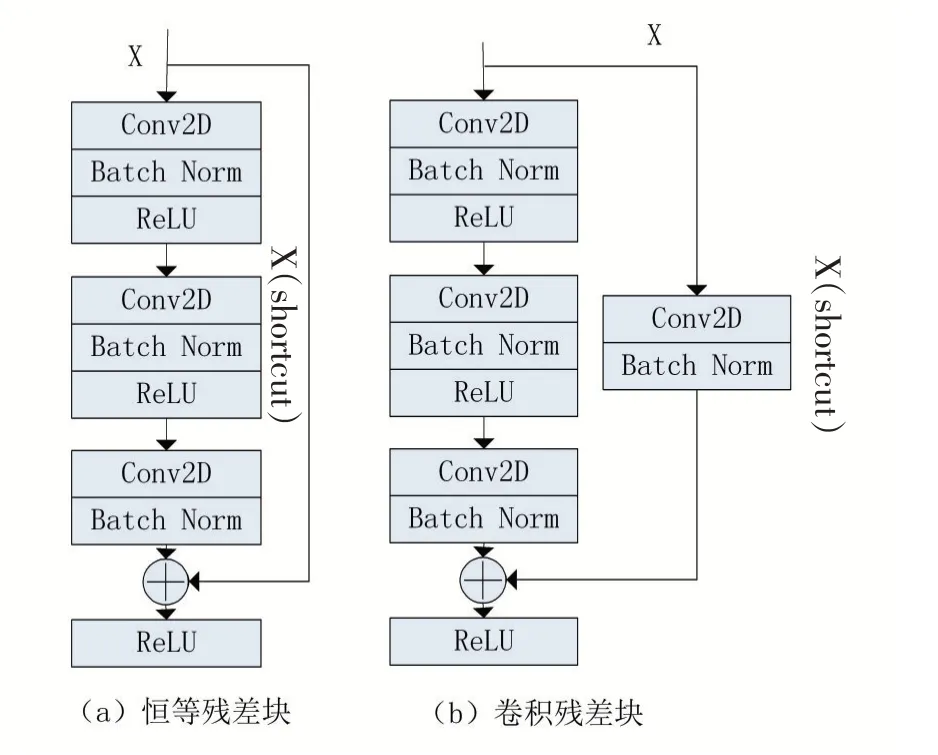
图5 两种残差块结构

3.2 DropBlock层

Dropout层是一种常见的正则化方法，在残差神经网络中一般应用与全连接层。Dropout每次迭代都会随机的使网络输入节点或者是上层网络的激活失效，相当于修改了网络结构，能够模拟不同网络结构的神经网络，提升网络模型泛化性和鲁棒性。为提升模型对变负载轴承故障检测的泛化性和鲁棒性仅在全连接层使用DropOut正则化是不够的，因此本文模型在卷积层后链接一个DropBlock层用以对卷积层的特征图（feature map）进行随机失活处理。Golnaz Ghiasi在文献[14]中认为Dropout正则化在卷积层中仅失活单个元素，而卷积层的特征图中相邻位置元素在空间上共享语义信息，网络仍可以通过其相邻元素学习到对于特征，因此提出一种新的正则化方法DropBlock，Drop-Block通过按块丢弃的方式将特征图中的语义信息成块失活，通过设置丢弃块的大小调整网络性能，当丢失块被设置为1×1时DropBlock将等效于Dropout。

3.3 全局平均池化层

CNN中使用全连接层将特征图转化为特征向量通过softmax层进行分类的方法存在权值参数过多的问题，有些网络甚至会有多个全连接层，而过多的权值参数会导致网络训练慢、过拟合等问题，为解决这一问题作者提出使用全局平均池化代替全连接，通过使用和feature map大小相同的平均池化窗口对整个feature map进行平均池化，一个feature map将输出一个参数进而从结构上对网络进行正则化防止过拟合。

4 本文模型

4.1 网络结构

本文提出的网络模型如图6所示。由残差单元组conv_x、池化层和分类层相连组成，其中残差单元组由卷积残差块、恒等残差块连接组成，每个卷积残差块、恒等残差块包含两层卷积核大小为3×3的卷积层。

图6 网络结构图

该网络模型的输入是3维数据，维度为（128，128，1）其中128×128为一个轴承样本小波变换后时频图的维度大小，1代表时频图是灰度图的形式。网络的输入首先使用卷积核为3×3的DropBlock层对数据进行随机失活，失活范围区间设置（0，0.5），不同批次的输入数据由于失活率是随机的因此模型具有更强的泛化性和鲁棒性。然后经过一个由64个7×7的大卷积核组成的卷积层对输入数据特征进行提取，同时添加批归一化层以减少数据分布带来的影响，在经过一层自动填充的池化尺寸为3×3均值池化层。然后经过4层残差单元组，每层残差卷积组之间使用池化核为3×3的平均池化层连接，最后通过全局平均池化层进行池化运算再通过失活率为0.5的Dropout层和维度为10的Softmax分类器得到故障诊断结果。

4.2 参数设置

具体的参数设置由试验和故障诊断领域的相关经验决定，池化层的数量都是和上层的残差单元层数量保持一致。DropBlock层的丢失块大小设置3×3保留率在0到0.5之间，Conv2D和均值池化层卷积核大小分别为7×7×64、3×3×64卷积步长均为2×2，Dropout层保留率为0.5。表3详细给出了每组残差卷积组的卷积参数设置。

表3 残差组参数设置

4.3 实验结果对比

为了验证本文提出模型中全局平均池化层和随机失活在相同工况和不同工况下对滚动轴承诊断的影响，在保持其他网络结构和参数不变的情况下，将使用全局平均池化层和随机失活的诊断准确度和去除全局平均池化层和随机失活的诊断准确度进行对比，为保证结果的有效性和准确性对两种网络结构均进行5次测试取平均值，对比结果如表4所示。

表4 全局平均池化和DropBlock对网络模型的影响

从表4中可以看到，在本文模型在相同工况下的准确度均略低于没有全局平均和随机失活的网络模型，平均降低0.11%。但在不同工况交叉验证的情况下诊断准确率均优于没有全局平均和随机失活的网络模型。从平均诊断准确度上看本文模型也更具优势。结果表明全局平均池化和随机失活在牺牲少量准确度的代价下减小了过拟合提高了网络的泛化性。

为验证本文提出模型的优越性，分别将本文所提方法在不同工况进行五次训练及测试，与文献[15]（离散小波变换+CNN，简称DWT+CNN）以及文献[16]（数据二维图像化+LeNet-5，简称IMA+LeNet-5）所提方法进行对比，对比结果如表5所示。

从表5中可以看到，本文方法仅在以0hp与3hp进行交叉验证时准确率分别为89.84%和92.68%，这是由于0hp和3hp样本数据分布差异过大导致，在其余情况下准确率均在95%以上。DWT+CNN仅在训练集为1hp交叉验证0hp时的准确率达到99.58%比本文方法高出0.38%，在其他情况下准确率均低于本文方法。IMA+LeNet-5在所有情况下不同工况下的准确率均低于本文方法，足以验证本文提出模型的优越性。

表5 经典模型效果对比

5 结语

本文为解决滚动轴承在不同工况下的故障诊断问题提出了基于小波变换联合残差神经网络的模型结构，利用小波变换将一维数据处理为二维时频图，暴露更多时频特性使网络更容易提取有效特征，同时对比传统残差的网络模型增添了平均池化层和DropBlock随机失活减小了过拟合具有更高的泛化性。

但是网络模型较大导致训练时间较长，提升不同工况诊断准确率是以牺牲少量相同工况诊断准确率为代价的，同时在数据分布差异较大的情况下准确率并不令人满意。希望在以后的研究中能简化网络模型同时进一步提高在数据分布差异较大的不同工况下的准确率。