基于平面立体的三视图绘制正等轴测图教学探析
朱仕成


摘 要:三视图是高中通用技术学科具有深刻内涵的技术图样语言,也是高中数学的重要内容。通过绘制正等轴测图来识读三视图是提高学生通用技术学科“图样表达”核心素养的重要载体。对通用技术《技术与设计1》苏教版教材中三视图、正等轴测图的教学内容重构,基于平面立体的三视图绘制正轴测图的教学中引入数学三维坐标(x,y,z)概念,创造坐标描点绘图法,实现二者互为转换的融合教学探索。
关键词:通用技术;三视图;正等轴测图;坐标
1 问题来源
“图样表达”是普通高中通用技术学科核心素养之一,是运用图样形式对意念中或客观存在的技术对象进行可视化的描述和交流[ 1 ]。 而三视图、正等轴测图已成为一种具有深刻内涵的图样语言,可以快捷、高效、丰富地呈现设计方案。能识读一般的机械加工图是学生用技术语言实现抽象与具体思维转换能力的重要评价指标。新版的通用技术《技术与设计1》苏教版教材将“绘制简单形体的正等轴测图”置于“绘制三视图标注尺寸”之后,增加了由叠加法绘制形体的正等轴测图来识读三视图的内容。弥补了旧教材对“绘制正等轴测图帮助学生识读三视图的作用”的忽视。同时,三视图作为高中数学新教材新增内容,曾是高考的常考知识点.识读三視图的试题经“考”不衰。很多学生能将“长对正,高平齐,宽相等”记得烂熟,也对简单几何体的三视图了如指掌,可处理这类问题时仍力不从心,无从下笔[ 2 ]。
平面立体的三视图还原是识读三视图的基本功。 如何帮助学生能从具体案例中抽象出识读三视图的一般方法,迅速实现由二维平面到三维空间的转换,从而发展学生空间想象能力呢?这一问题是所有高中通用技术老师和数学老师的聚焦点。笔者经过深入研究,发现引入坐标概念,基于平面立体的三视图绘制正等轴测图,应用坐标描点绘图法,具有简单易行、立竿见影的效果。
2 引入坐标概念
令正等轴测图的三维笛卡尔坐标(x,y,z)的x值为长度值,y值为宽度值,z值为高度值,原点o(0,0,0)。三视图中主视图所在坐标系为xoz,原点o(0,0)设置为过最右侧点的竖直线与过最下边点的水平直线相交点,x值为长度值, z值为高度值;相似的俯视图所在坐标系为xoy,原点o(0,0)设置为过最右侧点的竖直线与过最上边点水平线相交点,x值为长度值, y值为宽度值;相似的左视图所在坐标系为yoz,原点o(0,0)在设置为过最左侧点的竖直线与最下边点的水平直线相交点, y值为宽度值,z值为高度值。这样使三视图与正等轴测图之间通过坐标建立起一一对应联系,通过坐标描点绘图可以快速实现由二维平面到三维空间的转换。如图1所示是正立方体的三视图和对应的正等轴测图(伸缩系数简化为1,下同)。
在教学中,教师结合图1讲解正等轴测图三维笛卡尔坐标(x,y,z)的建立及其与三视图的对应关系。引导学生根据三视图投影规律“长对正、高平齐、宽相等”,准确标出正立方体正等轴测图中未标出坐标的轮廓线交点的坐标(x,y,z)。
评述:三视图三个视图的二维笛卡尔坐标系原点的设置是关键,必须明确使它们的“长、高、宽”方向的值与正等轴测图三维笛卡尔坐标(x,y,z)的“x值、y值、z值”相等。即正等轴测图的三维笛卡尔坐标(x,y,z)的x值为长度值,y值为宽度值,z值为高度值。 从而建立起二维平面到三维空间转换的桥梁。
3 绘制正等轴测图
基于平面立体的三视图绘制正等轴测图,可根据三视图上的基本尺寸采用坐标描点法绘制完成。
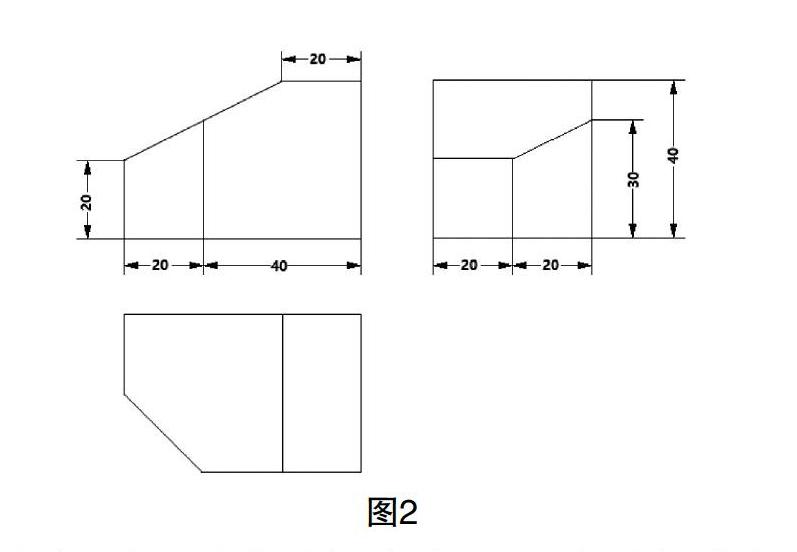
案例1:根据如图2所示平面立体三视图,画出它的正等轴测图。
其绘图步骤如下:
(1)根据形体的结构特征,建立三维笛卡尔坐标系,轴间角互为120°,z轴在竖直方向上,确定x轴、y轴、z轴在图纸上的位置。
(2)根据三视图的投影规律“长对正、高平齐、宽相等”标出各点的三维笛卡尔坐标(x,y,z)。按照 “抓主视,分线框,对投影,标坐标”的方法逐个标注各点的坐标。
(3)绘制坐标平面上的点,连接相应的轮廓线。如图3所示。在逐个坐标平面上按坐标进行描点,再用细直线连接。
(4)绘制坐标空间上的点,连接相应的轮廓线。如图4所示。作竖直线必须与z轴平行,用刻度尺或圆规截取高度。
(5)去除辅助线,虚化或去除不可见的轮廓线,加深轮廓线。
评述:该案例是由一个长方体通用两次切割形成的,在机械制图教学中一般采用“抓主视、按线框、对投影、想形状”的方法,绘制正等轴测图来还原三视图,这需要学生具有较强的空间想象力,并且熟悉基本几何形体的三视图,这对于空间想象力差、基础薄弱的学生有一定的困难。高中数学上常用的拔高法也相对较复杂。而上述笔者创建的坐标描点绘图法,对基础差的学生也能迅速绘制出来。
案例2:如图5所示是某三棱锥的三视图,画出它的正等轴测图。
分析:根据前述坐标描点绘图法建立正等轴图的三维笛卡尔坐标系;依据坐标(x,y,z)的x值为长度值,y值为宽度值,z值为高度值,以及三视图“长对正、高平齐、宽相等”投影规律,依次描出各点在坐标空间的位置,再对照三视图用直线段进行连接,如图6所示,最后去除辅助线、去除或虚化不可见轮廓线,加深轮廓线即可。
评述:该案例是一个简单的组合体结构,传统采用叠加法进行绘制,难点在于上方三棱柱的摆放位置。若弄不清三视图的方位关系,往往容易画错。而应用坐标描点绘图法则可一气呵成,有效避免类似的错误。
4 结束语
通过上述三视图、正等轴测图的融合教学,可以深化学生对三视图投影规律“长对正、高平齐、宽相等”的理解和熟练应用,辨析三视图与正等轴测图的关系,正确绘制简单形体的正等轴测图。在平时的课堂教学中,教师要关注学生的独立思考,给学生足够的思维时间或实践机会。特别是绘制图样的实践教学,不能只注重教师的讲,而忽视学生的学。教师要紧扣概念,通过实践引领学生深剖概念的内涵与外延,真正落实“做中学,学中做”的课程理念。
参考文献:
[1]中华人民共和国教育部.普通高中通用技术课程标准(2017年版)[S].北京:人民教育出版社, 2018:4-5.
[2]何业亮.割补法在三视图还原空间几何体中的应用[J].中学数学教学,2019(3):21-22.

