基于模型试验的重力式锚碇极限承载性能研究

李 薇，杨 华，尹小涛，乔文号，王 莹

(1. 云南交通职业技术学院，云南 昆明 650000；2. 中交铁道(武汉)建设科技有限公司，湖北 武汉 430071； 3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071)

0 引言

锚碇结构作为悬索桥荷载传递的终端，负责锚固承受巨大荷载的主缆，其承载能力和可靠性至关重要[1-3]。而重力式锚碇依靠自身承载，对周围环境的依赖性低，适应范围较广，既可适用于平地，也可用于山区，既能应用于岩性较好的场区，也适用于软弱岩层[4]。因此，重力式锚碇作为大跨度悬索桥锚碇的选型已经成为一种潮流和趋势。

随着国内外工程实践的积累，目前已经形成了一套相对保守的重力式锚碇勘察设计方法[5-7]。当前针对重力式锚碇承载性能研究主要包括试验研究、数值仿真和理论研究3个方面。试验研究方面主要通过现场摩擦试验和模型试验综合确定锚碇承载能力：赖允瑾[8]等以赣州赣江长江大桥为工程依托，开展现场原位相似试验，研究表明齿坎的存在能够改变基底的应力分布，减少锚锭的位移，大幅提高锚锭的承载性能并且最终改变锚锭的破坏模式。李永盛[9]等通过对江阴长江大桥北锚锭开展1∶100的室内相似模型试验提出了加强锚锭结构稳定性的措施，揭示了北锚锭的失稳模式为倾覆破坏；数值仿真模拟加载破坏全过程，得到应力变形分布特征和塑性区发展规律。林荣安[10]利用ANAYS有限元软件建立武汉阳逻长江公路大桥三维数值模型，研究各个部位应力分布状态，对锚锭进行优化并且对重力式锚锭工程进行综合安全评价。王龙飞[11]运用有限元软件建立香丽高速虎跳峡特大桥丽江岸重力锚模型，对荷载作用下锚锭的水平位移、竖向沉降、应力分布等进行分析，对重力锚各参数进行敏感性分析，为合理选择锚锭位置和主缆拉力设计提供理论指导。理论研究则主要依托于简化力学模型研究锚碇和地基的相互作用问题：尹小涛[12]依据悬索桥设计规范分析研究影响重力式锚锭安全评价的主要指标、计算方法和评价标准，提出了一种基于简化力学模型的重力式锚锭安全评价方法；朱栓来[13]分析了传统的抗滑稳定性系数法及分项系数法的现实及客观性，提出了锚锭设计采用分项系数法的合理性及必要性。当前基于传统摩擦承载重力式锚碇勘察设计方法相对保守，没有反映结构-地基联合作用的实际承载性能。

基于上述认识，本研究依托某特大桥左岸重力式锚碇工程，采用室内模型试验方法，评估重力式锚碇的承载性能，并提出反映锚碇倾覆失稳特性的转动指标，为类似工程的锚碇优化设计和安全评价提供借鉴。

1 工程概况

1.1 宣威岸重力锚工程概况

云南省某特大桥全长1 040 m，横跨宝山两个乡镇，主桥桥型采用628 m单跨双塔钢箱梁悬索桥，矢跨比为1/10,主缆横向布置2根，主缆横桥向中心间距为26 m，吊索顺桥向标准间距为12 m,主跨节段划分为(8.1+51×12.0+6.6)m，梁段最大节段重量约为140 t。

该特大桥左岸重力式锚碇工程，基底水平距离为56.0 m，单锚宽度为22.0 m，如图1所示。锚碇工程地质剖面如图2所示，主要覆盖层为第四系残坡积覆盖层、中厚层夹薄层白云质灰岩，支墩基底发育溶蚀沟槽，基底标高1 796.5 m；基底为中风化白云质灰岩，基底标高1 789.5 m。最大设计荷载为191 064 kN，支墩和锚碇底部摩擦因数分别为0.3和0.6，地基承载力容许基本值为500 kPa。勘察设计部门现场测定的岩土体参数见表1。

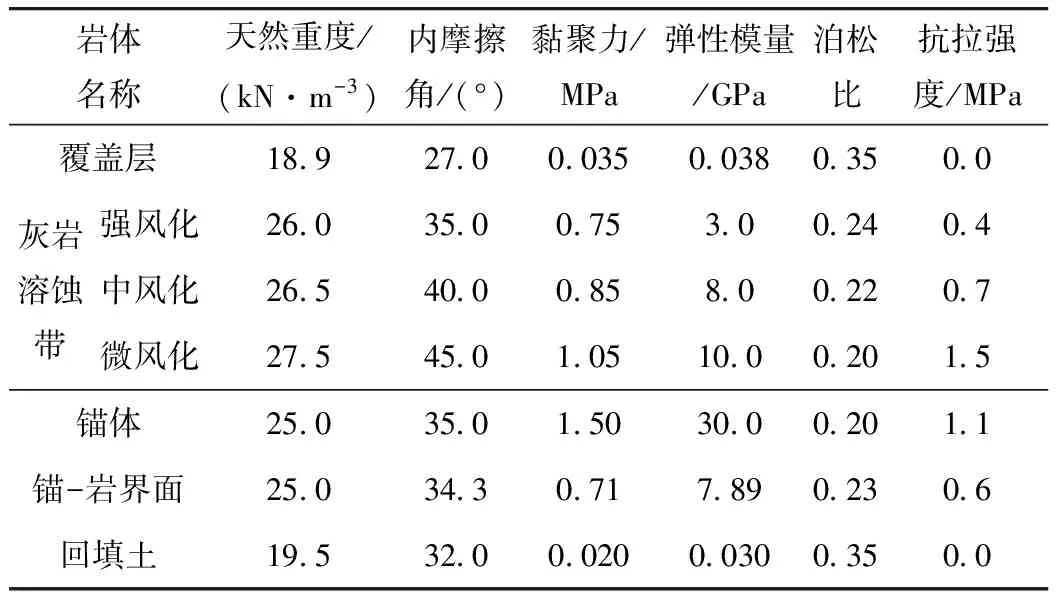
表1 锚碇和岩土体参数Tab.1 Parameters of anchorage and rock mass

图1 重力式锚碇几何尺寸Fig.1 Geometric dimensions of gravity anchorage

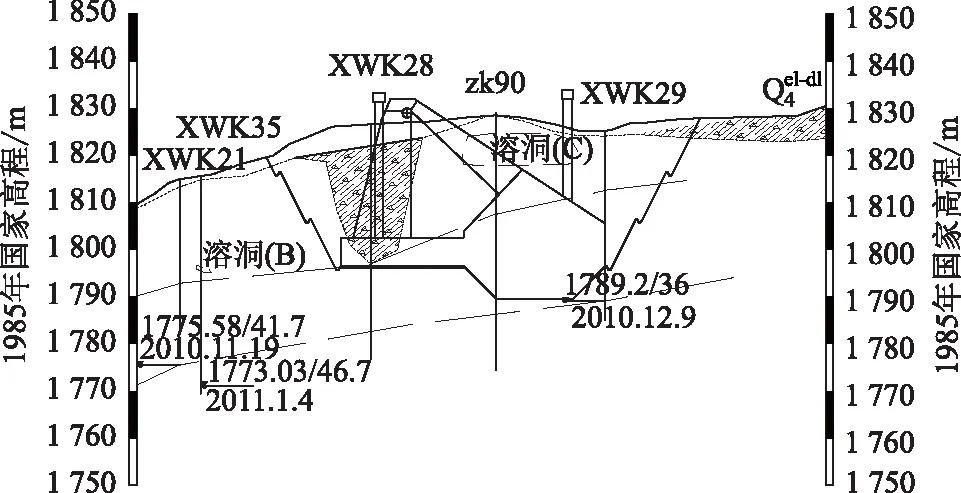
图2 重力式锚碇工程地质剖面Fig.2 Engineering geological section of gravity anchorage

1.2 重力式锚碇承载性能指标

根据《公路悬索桥设计规范》和《公路桥涵地基与基础设计规范》，与本次研究相关的重力式锚碇安全控制指标包括：在运营阶段重力式锚锭的水平位移不得大于主跨的0.000 1倍(即62.8 mm)，竖向位移不得大于主跨的0.000 2倍(即125.6 mm)。

2 基于模型试验的重力式锚碇承载性能研究

2.1 模型试验概述

根据实验室空间大小和试验需要，设计了长3.0 m、宽1.5 m、高1.0 m的模型箱，其结构如图3所示，通过定滑轮控制入射角和转向，垂向施加砝码控制分级加载。

图3 室内模型试验箱结构Fig.3 Structure of indoor model test chamber

试验中采用模型与原型的几何相似比为1∶100对锚碇系统各构件及锚体仅考虑几何缩尺，试验中混凝土拌和物的配合比为：水泥∶细碎石∶中砂∶水=430∶1 090∶210∶670。本次模型试验仅模拟单个锚体的受力状态，单个锚碇长56 cm，宽22 cm，高42 cm，如图4所示。

图4 模型试验锚碇构造Fig.4 Structure of anchorage in model test

地基岩体考虑了材料相似性。试验控制的相似参数统计列于表2。根据材料海选试验，确定含水率为5%且配合比为：重晶石粉∶石膏∶中砂=6∶6∶88的相似材料，符合强度参数控制目标，相似材料内聚力c=11.3 kPa，内聚擦角为φ=35°，弹性模量E为4.3 MPa，泊松比为0.27。

本试验进行的单锚试验，宣威岸重力锚的设计荷载为95 824 kN(简称1P)，单块折半则依据相似理论试验单级加载应该为47.9 N。在0～10P按照单级47.9 N加载，之后按照95.8 N加载直至锚碇显著失稳或者滑移为止，试验加载控制如表3所示。

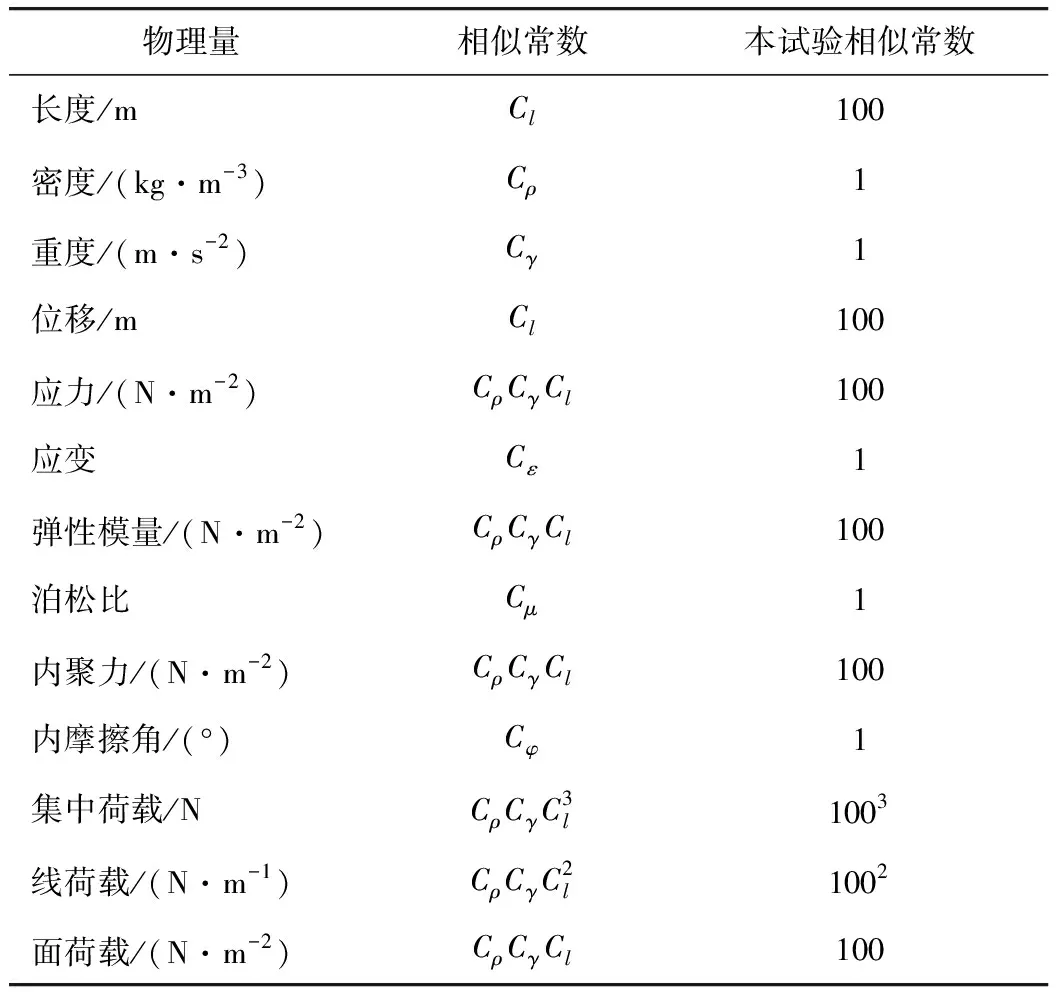
表2 本试验各相关量的相似常数Tab.2 Related similarity constants in test

表3 试验加载控制Tab.3 Load control in test

本次试验在锚碇基底埋设微型土压力盒、表观几何关键点架设电子千分表，测试模型见图5。

图5 模型监测点Fig.5 Monitoring points of model

2.2 变形指标揭示的极限承载性能

根据模型试验记录的位移数据，为探究锚碇位移随荷载增加的变化规律，将浇注好的锚碇模型置于事先分层填筑好的砂土上，利用钢丝绳模拟主缆，通过砝码进行加载，锚碇不同位置位移记录见表4。

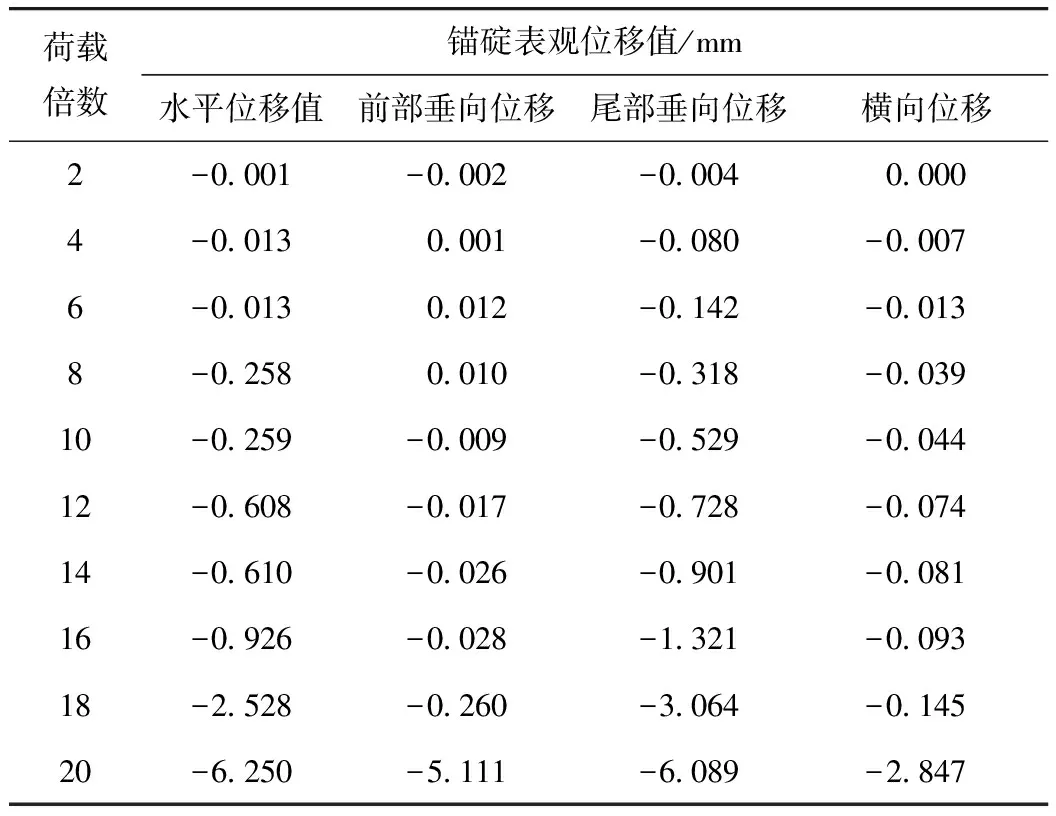
表4 荷载作用下锚碇位移值Tab.4 Displacement of anchorage under load

根据《公路悬索桥设计规范》，水平变位不大于62.8 mm，竖向变位不大于125.6 mm，根据相似比换算到本次模型试验水平位移不应大于0.6 mm，竖向位移不应该大于1.2 mm。由表2可知设计荷载作用下锚碇水平位移和竖向位移均满足规范要求；12P下水平位移0.608 mm，大于0.6 mm控制标准，可以认为满足水平位移的极限荷载为10P。16P时尾部竖向位移1.321 mm，大于1.2 mm控制标准，可以认为满足竖向位移的极限荷载为14P。横向位移和前部竖向位移不敏感，这也符合锚碇前倾受力的特点。

2.3 载荷曲线揭示的极限承载性能

将上述分析中相对敏感部位的荷载位移数据整理成荷载位移曲线，方便更直观地揭示锚碇的极限承载性能，如图6所示。

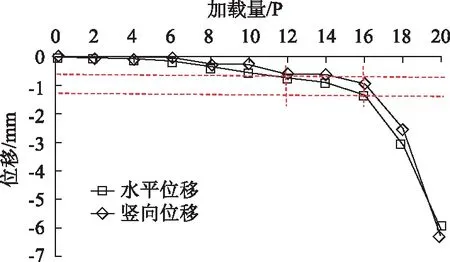
图6 锚碇位移随荷载变化曲线Fig.6 Curves of displacement of anchorage vs. load

锚碇的荷载位移曲线反映了锚碇在桥梁荷载作用下的运动变形特征，从荷载水平位移及竖向位移曲线可知，当加载量小于6P，锚碇自身的重量平衡外部荷载，锚碇自身位移很小，处于变形稳定状态；当加载量大于6P后，锚碇的表观位移逐步变大，可以认为锚碇产生了运动；当加载量超过16P后，锚碇位移急剧增加，锚碇有倾覆危险。因此，认定宣威岸重力锚的水平位移在12P时超过变形标准；竖向位移在14P时超过变形标准。按照保守原则，12P可以作为荷载位移曲线揭示的极限承载力。水平位移相对于竖向位移更敏感，所以重力式锚碇变形监测指标更应该侧重水平位移的监测和控制。

2.4 平底和齿坎带来的承载差异

传统的锚碇为平底或者斜底，均为摩擦承载，带齿坎的锚碇不但有摩擦承载，还有齿坎带来的支墩受力改善和齿坎夹持岩土体剪切承载，这些不但提升了锚碇承载性能，还改善了其受力，为了更好地论证齿坎的承载贡献，将同等水平投影面积的两类锚碇模型试验结果统计列于表5。

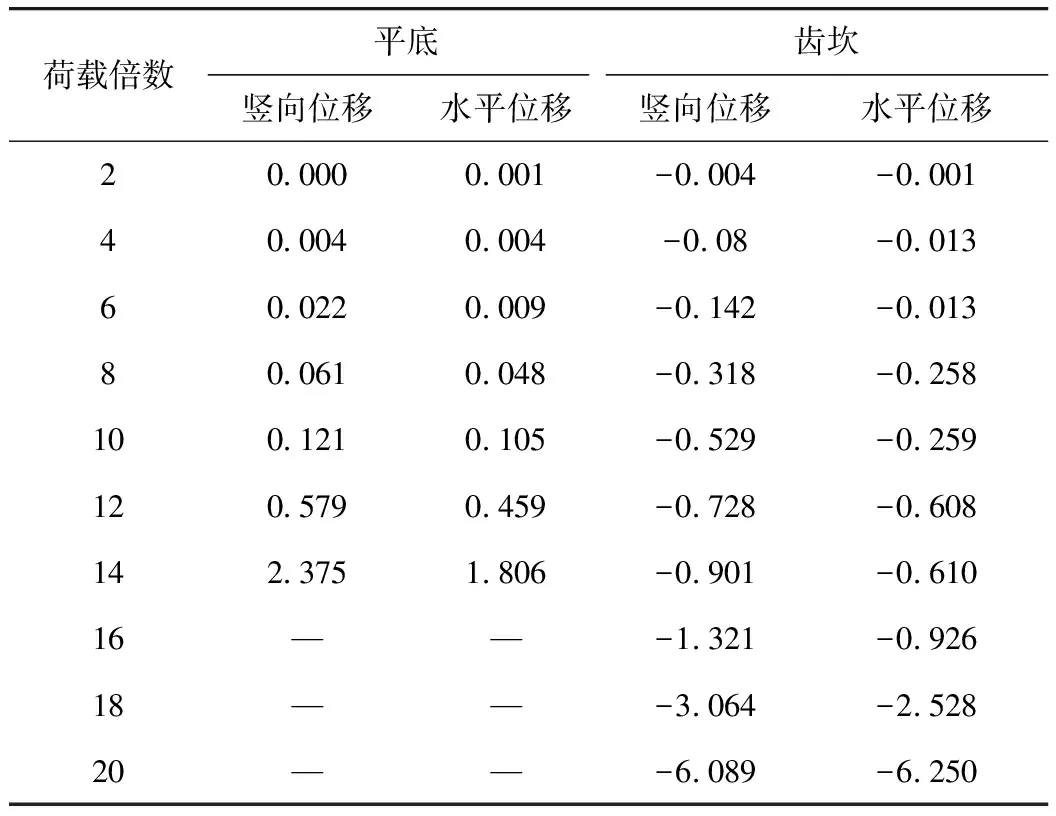
表5 荷载作用下锚碇水平位移值(单位：mm)Tab.5 Horizontal displacement of anchorage under load (unit:mm)

由表5可知，平底锚碇在14P之后，已经发生整体失稳，后续数据丧失。带齿坎锚碇达到极限之后，都能测到数据，这从侧面证明了齿坎锚碇相对于平底锚碇承载性能更优。

3 数值仿真验证

利用前面介绍的工程地质条件和锚碇尺寸信息，在Flac3D下建立数值模型，如图7所示，锚碇和周围岩体使用薄层单元连接，采用四节点四面体单元、八节点六面体单元和六节点五面体单元剖分网格，数值模型单元总数215 440个，节点总数为52 125。底面边界采用固定约束，侧面采用法向约束，地表自由。锚碇选用弹性本构，岩土体采用Mohr-coulomb的弹塑性本构，材料参数见表1。

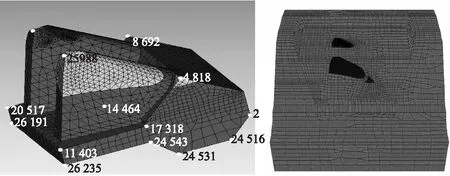
图7 重力式锚碇数值模型Fig.7 Numerical model of gravity anchorage

数值模型设计如下工况：初始应力平衡；基坑开挖；锚碇浇注；预应力施加2倍的设计荷载，设计荷载为95 824 kN，以面力的形式施加在前后锚面；采取和表3一样的加载工况，最终加载到20倍的设计荷载终止，每步施加荷载均计算平衡。数值计算所得结果见图8。

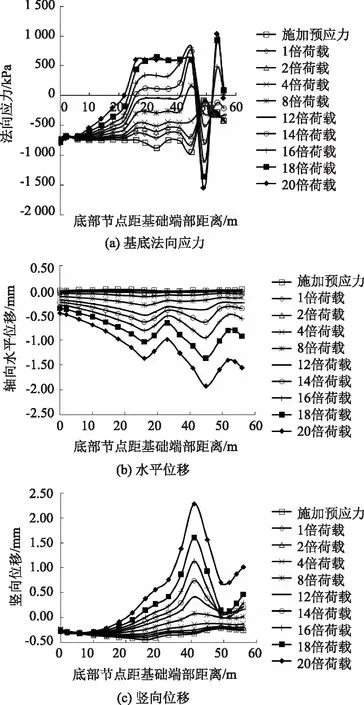
图8 重力式锚碇数值模型揭示的应力和位移曲线Fig.8 Stress and displacement curves presented by gravity anchorage numerical model

由图8可知，基底法向应力在12P之后，出现拉应力区；水平位移在12P之后出现增速，曲线变得稀疏。这些数据均佐证了模型试验结果的可靠性。

4 重力式锚碇承载性能综合探讨

本次模型试验遗憾的是基底应力数据没有测得，主要是模型尺寸造成的应力不敏感，但是数值试验的应力计算结果很有规律，首先模型试验检验了宣威岸重力式锚碇的极限承载力是否满足要求，同时揭示了不同变形指标的敏感性。在检验设计是否满足需要的基础上，为安全监测提供了指导。

通过笔者试验观测以及其他相关学者的研究经验得出[9-16]：齿坎型重力式锚碇的破坏模式多表现为锚碇产生前端下沉、后端隆起的刚性转动。

如图9所示，重力式锚锭在荷载作用下产生前后端不均匀沉降是锚锭整体失稳的主要原因，然而无论是抗滑稳定性指标、基底应力指标还是位移指标均无法准确反映重力式锚碇的这种转动倾覆趋势。可以参考地基基础设计规范表5.3.4对于20～50 m高耸结构(重力式锚碇高42.5 m)倾斜控制0.006，则不回填工况8P之前满足此控制标准；回填工况则在18P之前满足此标准，且回填对于倾斜的抑制可成倍减小，这说明结构没有倾覆稳定问题。倾斜值能够更好地表征结构转动倾覆稳定性。

图9 锚锭的前后不均匀沉降Fig.9 Uneven settlement at front and rear of anchorage

综上，宣威岸重力式锚碇在12P荷载下变形稳定，水平位移要比竖向位移敏感，倾覆稳定性需要增补倾斜控制标准，同时重力式锚碇-地基联合承载具有显著的阶段特征。

5 结论

(1)模型试验水平位移和竖向位移揭示的宣威岸重力式锚碇的极限承载力为12P。设计荷载下宣威岸锚碇变形稳定，安全储备较高。

(2)模型试验揭示带齿坎锚碇的整体稳定性要优于平底锚碇。

(3)模型试验和数值试验均揭示锚碇-地基联合承载的阶段特征显著，水平位移要比竖向位移敏感，倾覆稳定性需要增补倾斜控制标准。