基于优化VMD的悬索桥挠度温度效应分离方法

郑彩红，申 强，邓思勉，何小兵

(1.重庆交通大学 土木工工程学院，重庆 400074;2.山区桥梁与隧道国家重点实验室，重庆 400074; 3.交通运输部公路科学研究院，北京 100088)

0 引言

桥梁状态监测系统中实时挠度数据的温度效应分离是监测信息处理的一个关键问题，国内外学者对桥梁挠度成分分离进行了大量的研究[1-3]。Moyo等[4]利用小波变换对大跨度桥梁时间序列信号进行处理，以识别监测数据中的异常信号；李明等[5]根据信号的频谱特征利用经验模态分解(empirical mode decomposition，EMD)提取主梁挠度中的温度效应，通过建立温度与挠度的SVR模型计算挠度温度效应；刘纲等[6]使用粒子群算法，采用自适应调整滤波器的日温差信号和日温差响应信号的通带、阻带频率带宽方式消除温度效应；刘夏平等[7]采用LS-SVM建立以温度作为输入、挠度温度效应作为输出的非线性模型，分离出动态挠度中的温度效应。上述研究主要是以神经网络、支持向量机等机器算法和小波分析、Hilbert-Huang变换等信号分析方法来进行处理，其中小波分析需要考虑小波基的选择，自适应性差，不能做到在时域和频域上同时精确；EMD分解的自适应性强，但是存在端点效应及模态混叠现象[8]，同时还会产生虚假模态分量；EEMD在EMD基础上添加高斯白噪声以减轻EMD的模态混叠，但是添加噪声后信号会失真，正交性下降[9]。

Dragomiretskiy等[10]提出的变分模态分解(Variational Mode Decomposition，VMD)方法，其自适应性强，能够有效避免模态混叠现象，对采样和噪声都有较强的鲁棒性，已经被学者们用于信号去噪以及故障诊断等领域[11-13]，但在实时数据处理方面仍存在端点效应，影响处理效果。本研究提出3段交叉分解VMD端点效应改进方法，利用中心频率变化特征对VMD参数K，α进行优化，消除VMD分解所存在的端点效应；采用上述优化VMD算法对桥梁实测挠度进行信号分离，结合各个模态的中心频率和温度变化12 h和24 h的周期特性判定温度效应模态，将分离出的挠度温度效应和温度进行关联性分析，验证优化VMD算法运用于桥梁监测信息分离的有效性，实现桥梁实测挠度温度效应的精确分离。

1 VMD原理及优化算法

1.1 VMD原理

VMD方法摒弃了EMD中模态分量的循环筛选过程，将固有模态函数重新定义为幅频调制信号，其表达式如下[14]：

uk(t)=Dk(t)cos(φk(t))，

(1)

式中，uk(t)为第k个本征模态函数；Dk(t)为uk(t) 的瞬时幅值；ωk(t)为uk(t)的瞬时频率：φk(t)为uk(t)相位。

(2)

首先，将信号分解过程转移到变分框架，并通过不断迭代求其最佳值来确定每个模态分量的中心频率和带宽[15]。然后，使用逆傅立叶变换将各个分量返回到时域。最后，将原始信号的频域分解为K个频率带宽较窄的分量。变分问题的构造模型可以描述如下[16]：

(3)

式中，{uk}={u1,…,uk}代表VMD分解得到的K个IMF分量； {ωk}={ω1,…,ωk}表示各IMF分量的频率中心；δ(t)为单位冲激函数。

引入增广拉格朗日函数，以得到变分问题的最优解，多次迭代变分后使K个模态分量的带宽之和最小，从而得到VMD算法的最终结果[17-18]。具体步骤如下：

(2)n=n+1，执行整个循环；

(4)

(5)

(4)k=k+1，重复步骤(3)，直至k=K；

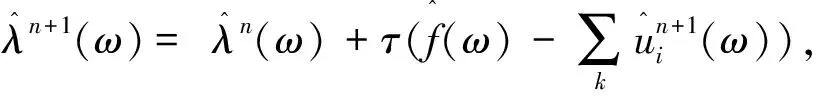
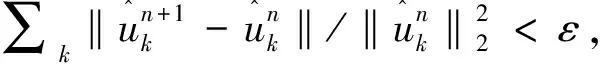
1.2 VMD算法端点效应消除

对于连续性信号，采用时间窗口在时间序列上滑动交叉进行VMD分解，原理上利用重叠部分分离效果较好段替换中间段端点部分，达到消除端点效应的作用。其具体构造步骤如下：

(1)分别对时间序列信号X1n={x1,x2,…,xn}，X2n={x1,x2,…,xn}，X3n={x1,x2,…,xn}进行VMD分解，其中X1n，X2n，X3n在时间上的排序如图1所示，图中椭圆区为对X2n进行VMD分解时出现端点效应的部位。

图1 信号时间分布Fig.1 Distribution of signals with time

(2)假设对目标信号X2n进行VMD分解后，信号两端各有m个数据点出现端点效应，分别用X1n，X3n经VMD分解后同部位的数据进行替换。具体公式如下：

(6)

式中，IMFk为对目标信号X2n各模态分量去端点效应后的第k个IMF分量；u1k(t1)，u2k(t2)，u3k(t3)分别是对X1n，X2n，X3n进行VMD分解后所获得的第k个本征模态函数。

(3)考虑到目标信号数据点数的不同是否会引起m值的变化，选择不同的采样长度n，对其进行VMD分解，得到不同数据长度下不同频率模态出现端点效应的m值，见表1。

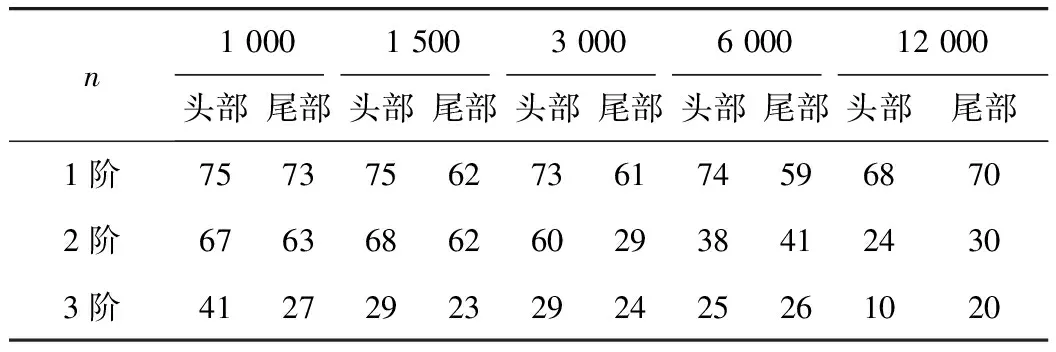
表1 不同n值对应的m

观察表1发现，随着数据长度n的增长，m值没有出现大幅度变化；随着频率的增加，m值逐渐减小；总体m值一直稳定在10～80之间，说明利用VMD进行分解时，端点效应主要出现在数据长度为10～80的两端。为了尽可能地保证数据分离精度，故拟定m值为100。

1.3 优化VMD算法的计算流程

消除端点效应的优化VMD算法的具体步骤如下：

(1)用VMD算法进行信号分解时，不同的分解模态个数K和惩罚因子α会对分解的效果产生影响，从而影响后续的分析结果。所以在进行VMD分解之前，首先根据中心频率的变化特征对关键参数K，α值进行优化。

(2)将优化后的参数代入3段不同时间段数据的VMD计算流程，结束循环后，每段数据被分成K个IMF分量。

(3)中间段数据各模态分量前后的100个数据点由前后时间段同模态重叠部分数据所替代，达到去除端点效应的目的。

(4)根据实际研究要求，选择合适的数据长度作为时间窗口，以同样的数据长度作为滑动步长，重复步骤(1)～(3)，达到实时数据的在线处理。

2 基于优化VMD的仿真与实测信号处理

2.1 3段交叉分解优化VMD仿真信号处理

对仿真信号进行3段交叉VMD分解，以验证前文所提出优化算法的有效性。定义一个合成信号x(t)如式(7)所示，采样频率fs=1 000 Hz，采样时间为1 s，在x(t)基础上加上信噪比为10的高斯白噪声，构成仿真信号x(t)(图2)。分别采用VMD，EMD对x(t)进行分解，结果如图3～图4所示。

(7)

图2 仿真信号组成Fig.2 Simulation signal composition

图3 VMD分解图Fig.3 VMD decomposition

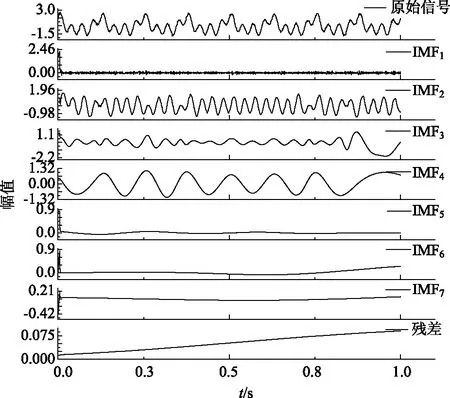
图4 EMD分解Fig.4 EMD decomposition

图3表明，VMD将输入信号分解成4个模态分量，其中IMF2，IMF3，IMF4分别对应于合成信号中的x1，x2，x3，噪声被分解成IMF1和残差。设各个模态分量IMFi+1=ui(i=1，2，3)，把VMD分解的各模态分量u1，u2，u3以及u(u=u1+u2+u3)与输入信号中的x1，x2，x3及x作对比。对比图5，u1，u2，u3以及u分别与x1，x2，x3及x在幅值以及频率大小上都相差不大，VMD分解有效避免了模态混叠现象，但是在分解信号的两端依然存在端点效应。观察图4，EMD将输入信号分解成7个模态分量，分量IMF2，IMF3，IMF4对应原信号中的x1，x2，x3，其余分量为虚假模态，由于噪声干扰，各模态分量被大量污染，分量之间出现模态混叠现象，两端有明显端点效应，信号分离效果较差。

图5 仿真信号与各模态对比Fig.5 Comparison of simulated signals with modes

综上，VMD分解虽然改善了EMD分解过程中的模态混叠现象，但仍存在端点效应。利用优化VMD算法对仿真信号进行处理，结果如图6所示。端点效应基本被消除，信号分离结果良好，验证了优化VMD算法对抑制端点效应的有效性。

图6 改进VMD各模态分量对比Fig.6 Comparison of modal components of improved VMD

2.2 桥梁监测数据分析2.2.1 工程背景

某长江大桥为钢箱梁单跨悬索桥，跨径布置为(250+880+250)m，两主缆中心距39.2 m；主塔为门式框架结构，基础采用分离式承台；两岸锚碇均为重力式锚碇，明挖扩大基础；加劲梁采用扁平流线型封闭钢箱梁，总宽42 m，梁高3.5 m。

本研究拟采用优化VMD算法对背景桥梁关键部位的实测挠度数据进行分离，验证该方法用于挠度与温度关联性分析的有效性。由于环境温度只在跨中截面有一个温湿度测点，样本数太少，不足以说明问题。观察结构温度与环境温度的时程曲线图，见图7，结构温度与环境温度的变化趋势基本一致。计算其相关性，环境温度与顶板温度相关系数达到97.01%，与底板温度相关系数达到99.09%，故决定采用结构温度来代替环境温度，对悬索桥挠度与温度进行关联性分析。

图7 温度时程曲线Fig.7 Temperature-time curves

本研究共选取了3个关键截面的测点，分别为1/4，1/2，3/4截面；挠度共选取了6个关键截面的测点，分别为1/8，1/4，3/8，1/2，5/8，3/4截面，温度和挠度测点布置如图8所示。

图8 测点布置Fig.8 Layout of measuring points

2.2.2 VMD算法的参数优化

VMD算法本质上相当于自适应维纳滤波器组，当分解模态个数K较少时，频率相近的模态会叠加在一起，即出现“模态混叠”现象；当模态个数较多时，会出现虚假分量，并且这些虚假模态还会影响到真实模态的分解效果。惩罚因子α是决定了信号重构的保真度，α越小，数据保真度越高，但是受噪声影响也越大；相反α越大，有用信号的完整度就得不到保证。因此，在VMD分解之前，需进行参数优化，具体步骤如下：

(1)结合小波分析对原数据进行去噪，以信噪比SNR、均方根误差RMSE判定去噪效果[19]；

(2)计算不同K，α值下的中心频率；

(3)根据中心频率变化特征选择合适的K，α值。

拟选取跨中截面下游测点ND42一月份的实测挠度数据进行VMD分解，不同模态个数K值、不同惩罚因子α值下的中心频率如表2所示。

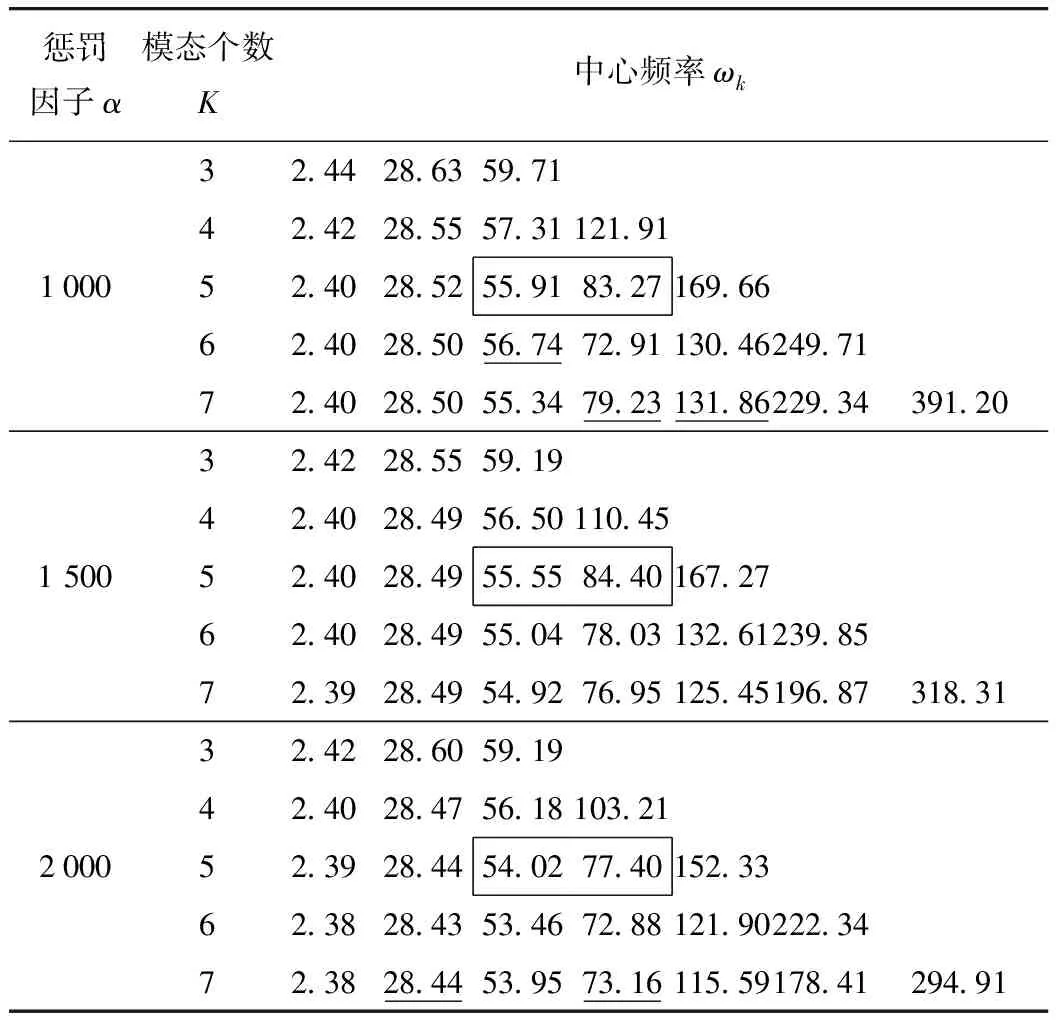
表2 不同K值、α值对应的中心频率

从表中可以发现，随着模态个数的增加，频率带宽逐渐变窄，高阶频率分解得越来越精细，前3阶频率随着模态个数的增加数值基本稳定。1阶频率为2.4，对应低频趋势项；2阶频率为28.5，接近1个月30 d，对应于24 h温度变化；3阶频率为55.5，接近2阶频率的两倍，对应于12 h温度变化；其他更高阶频率对应与汽车、风荷载等随机荷载。钢箱梁悬索桥实测挠度数据温度效应低频特性显著，K选取需满足低频信息的有效分离。实测挠度数据预处理后的FFT变换(图9)表明，悬索桥低阶频率与文章中所分析的3阶低频模态频率相符合(表2)。因此，K值的取值只需满足前3阶低频模态的分离即可。表2显示，当模态数大于等于5时，前3阶模态中心频率逐渐稳定，推荐K值至少取5。如关注高频信息，K值可取更大(需根据研究需求，进行进一步优化)。

图10 不同K的中心频率变化曲线Fig.10 Central frequency curves corresponding to different K values

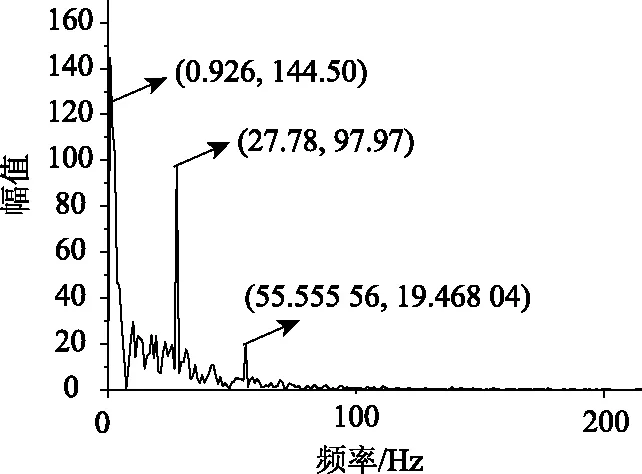
图9 挠度FFT频谱图Fig.9 FFT spectrum of deflection

惩罚因子α用于噪声抑制。当α过小，噪声未被有效抑制，会导致中心频率的波动(见表2，α=1 000)；当α过大，更多有用信息被抑制，同样会出现波动(见表2，α=2 000)，需要进行反复试算优化。优化表明，当α=1 500，高阶中心频率规律显著，噪声抑制效果好。同时，分别计算不同α取值下第3阶模态和第4阶模态之间的中心频率之差，发现α=1 500时中心频率之差最大，频率带宽更窄，满足前3阶分离要求，故推荐α=1 500。

综上所述，上述推荐的K与α取值满足钢箱梁悬索桥实测挠度温度效应分离(低频效应)。α=1 500时，随着模态个数的增加，中心频率的变化曲线见图10，从图中也可看出，模态个数越大，曲线变化越平缓，高阶频率分解得越精细，可见优化VMD算法可能也有利于后面对高频信息的分析，本研究不做过多探讨。α=1 500、K=5的中心频率变化曲线见图11，各分离模态的中心频率变化曲线独立，未出现相交情况，分离效果可以得到保证。

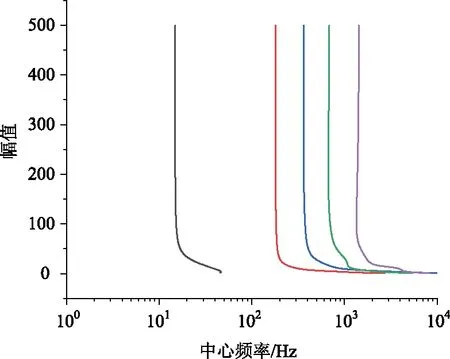
图11 中心频率的变化曲线Fig.11 Central frequency change curves

2.2.3 实测挠度数据的各成分分离

为验证本方法在实际应用中的有效性，采集背景桥梁实时监测挠度和温度3个月的数据，利用优化VMD对桥梁的各挠度成分进行分离。采集时间段为2019年1月1日00:00:00至2019年4月1日00:00:00，采样间隔为10 min/次。挠度和温度每一个月的数据各形成一组样本，挠度和温度分别有3组样本。温度每组样本中包含3个截面12个温度传感器的数据，挠度每组样本中包含6个截面12个传感器的数据。运用优化VMD算法对各测点30 d的挠度信号进行分离，去端点效应后的分离结果如图12所示。

如图所示，原始挠度信号分离成5个IMF分量以及一个残差项，其中残差项是高频噪声，IMF1和IMF2为平稳高频信息，应是汽车荷载或其他随机荷载引起；IMF3和IMF4所对应的周期分别是12 h和24 h，结合前文的中心频率可以判断IMF3和IMF4都是由温度引起的，即温度效应，IMF5为由长期温度引起的趋势项。为了进一步证明所分离结果的准确性，分别提取分量IMF3，IMF4，IMF5以及它们的组合IMF45(IMF45=IMF4+IMF5)，IMF345(IMF345(=IMF3+IMF4+IMF5)与所对应的同时段的顶板温度进行对比，求其相关系数，进而判断其相关性。经计算对比，只有将3个模态分量组合起来其相关系数最高，各截面温度与挠度分离信号相关系数见表3，挠度分离信号与温度对比图见图13。

图12 实测挠度数据VMD分解图Fig.12 VMD decomposition diagram of measured deflection data

其中，Cov(X，Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差。

表3中，各测点分离结果与温度的相关系数基本都在90%～99.51%之间，观察图13，也可以说明分离效果良好，基本印证前面所提出的判断，即IMF3～IMF5均是由温度引起的挠度。在表中有几处测点的分离数据与温度的相关系数低于90%，可能是由于传感器故障或者计算误差造成。

表3 挠度分离信号与温度相关系数

图13 挠度数据分离结果与温度对比Fig.13 Comparison of separated deflection data and temperatures

2.2.4 同截面实测挠度分离温度效应对比

由于只取了1/4，1/2，3/4截面的温度数据，故1/8，3/8，5/8截面的温度效应分离准确性由同截面上下游两处测点的分离结果来进行判定，因为同截面的两侧点处于对称位置上，理论上应该处于同一温度场，两侧点的温度效应应该相同[20]，将1/8，3/8，5/8截面两侧点处分离出的温度效应进行对比，其相关系数见表4，挠度分离信号对比见图14。观察表4和图14，可得出结论：同截面两侧测点实测挠度温度效应相关系数均达到98%以上，接近100%，对比图中，两侧挠度温度效应线型基本相似，可以说明优化VMD分离效果良好。

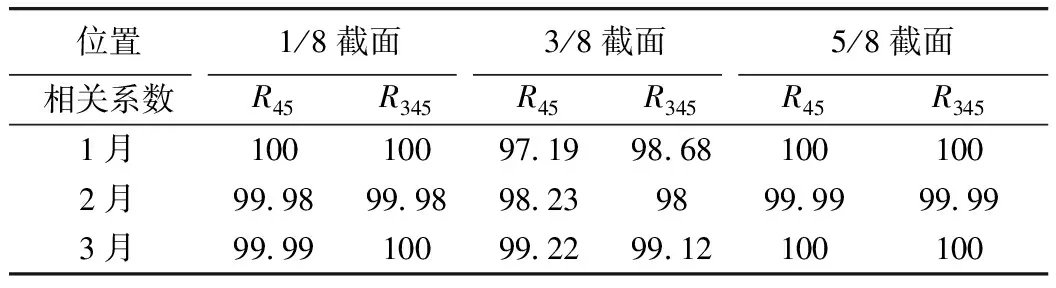
表4 同截面挠度分离信号相关系数

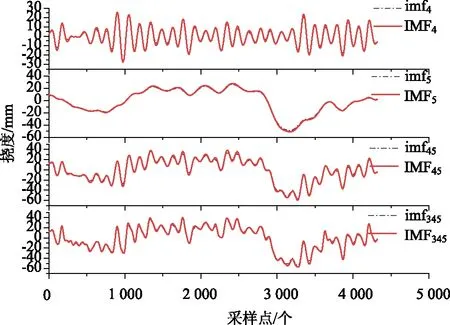
图14 同截面两侧挠度数据分离结果对比Fig.14 Comparison of separated deflection data on both sides of the same section

悬索桥实测挠度数据的分离结果证明：钢箱梁悬索桥温度挠度效应非常显著，长期温度荷载作用下的桥梁结构响应大于活载效应，活载作用下的结构动态响应及结构损伤信息极易被“淹没”，桥梁健康监测信息处理研究中进行温度效应分离对评价结构的健康状况评价至关重要。优化VMD分解方法适用于钢箱梁悬索桥挠度实时数据温度效应分离，识别活载效应及其损伤状况，并且可以用于挠度温度效应的趋势预测。

3 结论

采用本研究提出的优化VMD方法对某长江大桥实测挠度数据进行了分离，对悬索桥主梁挠度与结构温度进行了关联性分析，主要结论如下：

(1)VMD信号分离减轻了EMD和EEMD分解信号所存在的模态混叠问题，研究得到了不同数据长度下VMD分解出现端点效应的m值，并利用3段交叉分解对其进行消除。

(2)对改进3段交叉分解VMD方法，采用中心频率进行参数优化，成功实现不同频率信号的分离，可用于实时数据的处理。

(3)以某悬索桥为研究背景，进行了实测数据分离，得到了挠度温度效应，发现温度产生的挠度比随机荷载产生的挠度要大2个数量级，并对其进行挠度-温度相关性分析，验证了论文所提出的方法能够用来分离信号，反映各响应与各因素之间的关联性。

(4)在对VMD算法进行参数优化时，发现随着模态数的增加，高频信息被分离得更加精细，是否能把VMD算法运用到由汽车等随机荷载引起的高频信息中，还有待进一步的研究。