基于GSL&PS-PGSA的钢拱架结构设计优化研究
刘宇
(湘潭交通发展集团有限公司, 湖南 湘潭 411100)
随着钢筋砼拱桥在西南山区的大力推广,钢拱架现浇施工迎来飞速发展,对钢拱架结构受力性能的研究也日臻完善。张猛等以湖南某钢筋砼拱桥为背景对钢拱架的选型设计、拼装、受力性能等进行了探讨;王诗青等研究了不同钢拱架截面形式对其受力性能的影响效应;袁鹏等采用弹性-刚性支撑法确定了钢拱架吊装预抬高值;常柱刚等研究了主拱圈和钢拱架联合作用时钢拱架结构的受力特点,并与拱架单独受力进行了对比分析。在钢拱架结构设计优化方面,牟洪仲等对比分析了2种不同弦杆长细比的钢拱架结构在施工中的受力规律,得到了钢拱架结构的新构造形式。该文以贵州某钢拱架现浇施工的钢筋砼拱桥为工程背景,基于生长空间限定与并行搜索的算法组合新机制(GSL&PS-PGSA算法),结合MIDAS仿真计算分析,对钢拱架结构进行设计优化分析。
1 工程概况
贵州某钢拱架现浇施工的钢筋砼拱桥,主拱净跨125 m,净矢高25 m,净矢跨比1/5。拱圈采用悬链线,拱轴系数为2。主拱圈为单箱二室截面,截面高2.2 m,顶、底板厚25、35 cm,腹板厚35、40 cm。
主拱圈采用钢拱架现浇施工,钢拱架结构布置见图1、图2,各构件材料参数见表1。采用特制专用可调式钢拱架,采取从拱脚分节段逐步向拱顶推进的施工顺序,沿弧向共有2个拱脚节段、20个标准节段和拱顶合龙段,钢拱架结构对称,各节段横向布置10片贝雷梁。拱架顶、底面采用水平平联杆连接,横向联系采用横联杆;各节段间下弦杆采用阴阳接头连接,上弦杆采用连接杆连接。拱脚节段拱脚处为钢管铰,与临时拱座上的半圆铰座配合安装,钢拱架采用斜拉扣挂悬拼施工。
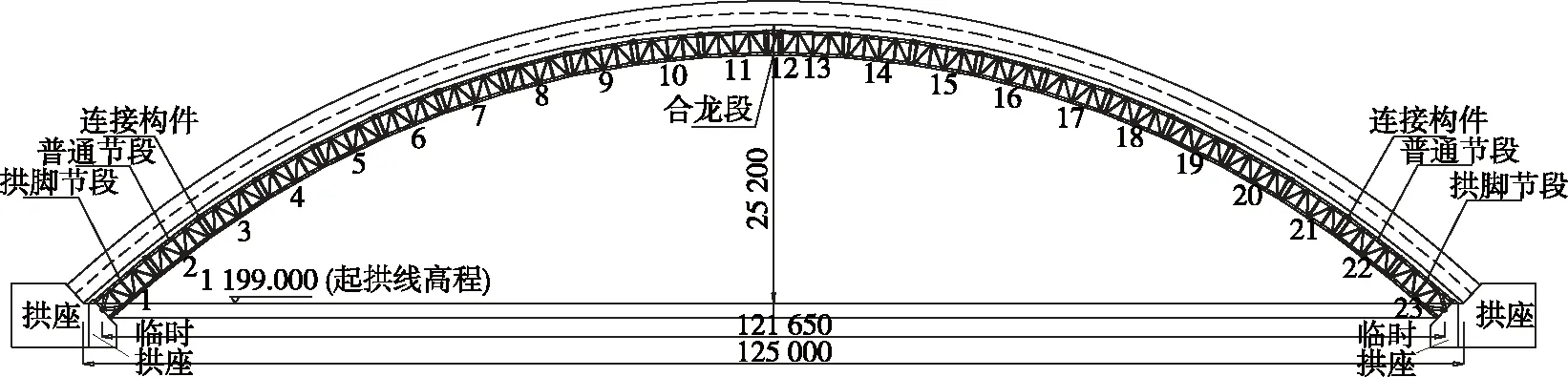
图1 钢拱架立面布置(单位:高程为m,其他mm)
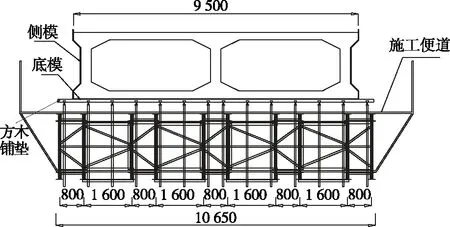
图2 钢拱架横断面布置(单位:mm)

表1 钢拱架各构件材料参数
2 基于GSL&PS-PGSA算法的结构优化
2.1 GSL&PS-PGSA算法基本原理
PGSA(模拟植物生长算法)以植物形态素浓度理论即其向光性机理作为启示准则,把植物的整个生长空间当作优化问题可行域,将生长空间中的生长点作为优化问题的设计变量组合,优化问题的最优值为离光源最近的生长点所对应的目标函数值。在光照作用影响下,各生长点会聚集形态素,离光源越近,可生长点的形态素浓度则越高,其生长概率便越大,且形态素浓度在每次可生长点生长后会重新分配。PGSA算法以植物形态素浓度在生长过程中的分布规律作为搜索机理。形态素浓度计算公式如下:
(1)
式中:ηm,j为第j个可生长点的形态素浓度;f(x0)为初始目标函数值;f(xm,j)为第j个可生长点对应的函数值;m为可生长点集合;n为集合m中可生长点的总数目。
传统的PGSA优化算法步长单一,搜索机制不足,计算效率低。为此,采用融合并行搜索机制的GSL&PS-PGSA算法。其基本原理及主要特征如下:1) 每次新增可生长点时,采用多种步长混合并行搜索方式,大步长以步域比U(大步长与可行域跨度之比)为表征,负责距离较远新增可生长点的搜索,小步长负责所选生长点附近新增可生长点的搜索。2) 在可生长点集合m中加入新增可生长点更新集合前,先判断各新增可生长点对应的各目标函数值是否劣于集合m中最劣质的生长点目标函数值,剔除劣质可生长点,将优质新增生长点加进集合m,从而增大选中可行域跨度中优质可生长点的概率,也为算法提供有效终止机制。3) 每次生长点每次选择前,控制集合m中可生长点个数上限为n个,对各可生长点的目标函数值排序,取目标函数值较优的前n个可生长点作为新生长点集合。通过劣质可生长点的剔除,提高算法的计算效率。
2.2 钢拱架结构优化模型
钢拱架结构复杂程度较高,一般无法采用具体的显示函数对目标优化函数进行表达,在工程结构优化问题分析中,常采用转换为抽象数学模型的方式对结构优化问题进行分析或求解。数学模型主要由结构目标优化函数minf(x)、结构优化设计变量x及结构优化约束条件Qi(x)组成。
(1) 目标函数minf(x)。一般用目标函数最小值的问题代替直接求解结构优化问题。对于钢拱架结构材料用量最优化问题,以钢拱架结构总质量作为目标函数minf(x)。
(2) 优化设计变量x∈X;x=(x1,x2,x3,…,xn)。对于空间结构,一般可取其结构各几何参数、结构形状及截面特性等参数作为优化设计变量x。对于钢拱架空间结构,按其节段纵向分为23个部分,取各部分构件的截面编号为优化设计变量x。
(3) 约束条件Qi(x)≤0;i=1,2,3,…,m。对于空间结构,一般以结构刚度指标、强度指标及稳定性指标等作为结构优化问题的约束条件。对于钢拱架结构设计优化问题,取钢拱架在拱圈砼浇筑过程中的容许变形作为约束条件1,强度设计值作为约束条件2,局部构件及整体稳定性作为约束条件3。
2.3 钢拱架结构优化流程
借助Fortran和MIDAS数据交互方式实现基于GSL&PS-PGSA的钢拱架结构优化。先利用Fortran编制GSL&PS-PGSA优化算法并输出设计变量取值,再将算法输出的设计变量取值代入MIDAS仿真分析软件中进行结构优化目标函数求解,并利用前述约束条件判定各参数指标,利用Fortran和MIDAS的数据循环交互实现钢拱架结构的设计优化(见图3)。

图3 钢拱架结构优化流程
3 钢拱架结构仿真模型的建立
采用MIDAS/Civil对钢拱架结构进行模拟分析,定义桥梁纵向为全局坐标系的X轴、竖向为Z轴、横桥向为Y轴。整个钢拱架离散为4 051个节点、12 536个单元。钢拱架各节段的下弦杆节点间采用释放连接节点弯矩的方式模拟阴阳接头的连接即铰接,拱架其他各杆件间的连接均采用共节点固结连接。考虑结构自重、砼湿重、模板、人工机具及冲击、振捣等临时荷载,分析拱圈砼浇筑全过程中钢拱架的力学性能。仿真分析模型见图4。

图4 钢拱架仿真分析模型
4 钢拱架设计优化分析
根据钢拱架结构安装方法及受力特性,将钢拱架纵向按节段分为23组作为设计变量的数目,每组截面形式按各构件不同分别设置不同截面,上下弦杆采用双拼开口槽钢,竖腹杆及斜腹杆采用方钢,水平平联及横向联系杆件采用角钢。选择钢拱架结构各构件常用截面形式库进行优化设计分析,各组杆件许用截面见表2。

表2 各组杆件许用截面
以每组钢拱架构件的截面编号作为设计变量;优化目标为钢拱架结构总重;以钢拱架在拱圈砼浇筑中的挠度限值、应力限值、稳定性要求及各构件的许用截面形式作为约束条件,其中挠度、应力限值及构件稳定性计算根据GB 50017-2017《钢结构设计标准》中相关规定进行。利用前述基于GSL&PS-PGSA的编程及MIDAS计算分析模型进行优化分析,各构件初始截面按表1中原设计各杆件参数取值,钢拱架初始结构总重为306.6 t。
4.1 钢拱架设计优化结果
钢拱架各构件截面优化结果见表3。钢拱架结构设计优化后,结构总重为260.3 t;在砼浇筑过程中,钢拱架最大下挠为74.52 mm,最大应力为-142.23 MPa,稳定性计算结果为N/(φAf)≤1,均满足GB 50017-2017的要求,即满足约束条件。

表3 钢拱架各构件截面优化结果
4.2 优化前后结果对比分析
钢拱架结构优化前后各构件最大应力对比见表4,钢拱架结构变形对比见表5。
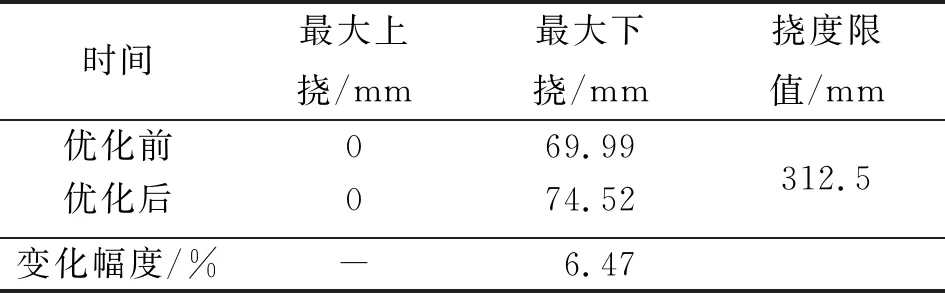
表5 优化前后钢拱架结构变形计算结果对比
由表4可知:优化后钢拱架结构上弦杆最大应力由-122.8MPa变为-128.91MPa,下弦杆最大应力由-134.92 MPa变为-142.23 MPa,竖腹杆最大应力由-121.08 MPa变为-119.74 MPa,斜腹杆最大应力由-96.29 MPa变为-100.67 MPa,水平平联杆最大应力由79.99 MPa变为72.55 MPa,横联杆最大应力由-85.87 MPa变为-91.14 MPa,最大变化幅度为-9.30%。优化前后钢拱架各构件最大应力均满足约束条件。

表4 优化前后钢拱架结构应力计算结果对比
由表5可知:优化前后钢拱架结构最大上挠均为零,最大下挠分别为69.99、74.52 mm,变化幅度为6.47%。优化前后钢拱架变形均满足约束条件。
5 结论
基于GSL&PS-PGSA算法,结合MIDAS仿真模拟计算,以钢拱架结构自重为目标优化函数对钢拱架结构设计进行优化分析,主要结论如下:
(1) 钢拱架结构自重优化后,结构自重由306.6 t降为260.3 t,降幅为15.1%,大幅提高了钢拱架结构使用的经济合理性。
(2) 钢拱架结构设计优化后,上下弦杆、斜腹杆及横联杆最大应力增大,竖腹杆及水平平联杆最大应力减小,最大变化幅度为-9.30%;钢拱架变形由69.99 mm增加至74.52 mm,变化幅度为6.47%。整体钢拱架受力性能未发生明显变化,但提高了构件材料强度使用的利用率。
(3) 优化后,钢拱架结构各受力性能均满足规范要求,验证了GSL&PS-PGSA算法在工程结构优化问题中应用的可靠性及适用性,可推广使用。
--先进无机材料论坛例记(Ⅱ)
--先进无机材料论坛例记(Ⅰ)

