Kalman滤波算法研究及其在高铁沉降监测中的应用

焦雄风 谭社会 张献州 陈 铮 郑旭东

(1.西南交通大学地球科学与环境工程学院,成都 611756; 2.中国铁路上海局集团有限公司,上海 200071; 3.西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,成都 611756)

1 概述

近年来,随着运营高速铁路逐渐增多,如何对其沉降监测数据进行科学有效的分析是目前许多学者研究的问题。Kalman滤波是一种处理实时动态数据的线性递推算法,其特点是能减少数据中存在的随机误差,还原数据中包含的有效信息。马龙将Kalman滤波算法应用在运营高速铁路重点地段变形监测数据的分析中,探究Kalman滤波在数据降噪方面的效果[1];雷孟飞等研究自适应Klaman滤波在北斗卫星数据分析中的应用,为处理分析卫星获取的运营高速铁路变形监测数据提供思路[2];杨保岑将Klaman滤波集成于大跨桥梁监测系统中,为运营高速铁路在桥梁段的变形监测数据分析提供参考[3]。运营高速铁路沉降变形受多种随机干扰因素影响,如风速、温度及建成时间等[4]。针对不同随机干扰因子,应建立具体对应的kalman滤波模型,以分析不同环境下的运营高速铁路沉降监测数据。

通过设置不同的随机干扰因子,建立Kalman静态、常速、加速滤波模型,并将其应用于运营高速铁路初期,中期、趋于稳定期状态下的沉降监测中,通过平均绝对误差、均方根误差等[5]相关模型精度评价指标,对滤波值进行评估。

2 算法原理

2.1 Kalman滤波工作原理

Kalman滤波的动态方程及观测方程为

式中,xk为(n×1)初值参数矩阵;zk为(m×1)监测参数矩阵;wk为(n×1)动态噪声;vk为(m×1)监测噪声;Φk/k-1为(n×n)状态转移矩阵;Hk为(m×n)观测矩阵;Bk/k-1为(n×r)控制参数的增益矩阵;uk-1为(r×1)控制参数矩阵,下标k表示第k时刻在某一时刻的估值。X可进行如下递推演

估计误差协方差矩阵一步预测为

测量误差为

测量误差协方差为

最优卡尔曼增益为

更新的状态估计为

更新的协方差估计为

若给定初值状态参数以及在k时刻下的观测值Zk,就能得到在k时刻下目标状态的一步预报值^xk/k-1和估值xK。算法流程如图1所示。

图1 Kalamn滤波算法原理

2.2 随机干扰因子的设置

静态模型随机干扰因子设置:只注重观测点的位置X为状态参数,监测点位置瞬间变化看作随机干扰[6]。初值X0取第一期监测数据,而初始方差阵P0、Rk取第一期监测数据对应的方差阵[7],其大小依据不同监测项目的监测方法和精度确定;过程噪声Qk可根据经验计算确定[8]。

常速模型随机干扰因子参数设置:将监测点的位置和变化速度速率作为状态参数,瞬间加速度视为随机干扰[9]。取第一期平差后测点位置X0作为监测点初始位置;取第一期、第二期的平均变形速率̇X0作为观测点初始变化速率[10],即

Rk的设定与静态模型初值设置相同,过程噪声Qk可设置为

q根据文献[11]设置;初始协方差矩阵P0可设置为

加速模型初值参数设置:将观测点的位置X、变化速率、加速度作为状态参数,加速度的瞬间变化率视为随机干扰,即

观测噪声Rk取第一期监测数据的相应方差阵,过程噪声Qk随着时间间隔的不同而发生改变,可以表示为

初始协方差矩阵P0可设置为

式中,DẊ0=

Kalman滤波初始状态的参数选择应考虑变形体建成时间,以及周期观测频率[12]。若变形体处于建成初期,变形相对较快,观测数据波动大,Kalman加速滤波模型能顾及观测点的变化速率和变化加速率;若变形体处于变形趋稳期,波动性较小,Kalman常速滤波模型可顾及观测点的变化速率;若变形体处于变形后期,即变形稳定期,可仅将监测点位置作为状态参数,可参考Kalman静态滤波模型的参数设定进行分析。

2.3 模型精度评价指标

根据上述参数设定,理论上滤波精度不会出现失真现象[13]。实践中,噪声因子以及真实数学模型往往很难确定[14],故引入单位权方差[15](σ2)、均方根误差(RMSE)[16]、平均绝对误差(MAE)来进行具体滤波精度评价,均方根误差(RMSE)能具体反映估值与监测值之间的偏差,其值越小表明其滤波模型抗干扰能力越好;单位权方差σ2、平均绝对误差(MAE)能反映估值误差的实际情况,其值越小,表明滤波模型拟合程度越高。这三者常作为模型预测结果量化的准则之一[17],有

式中,n为观测期数;νk为监测值与预报值的差值。

3 实例分析

某高铁沉降监测地段全长1.5km,位于平原地区,年度降雨量较充沛。该段共布设33个监测断面,每个断面设7个监测点,取3个不同断面上的监测点累计沉降数据进行分析,基本信息见表1。

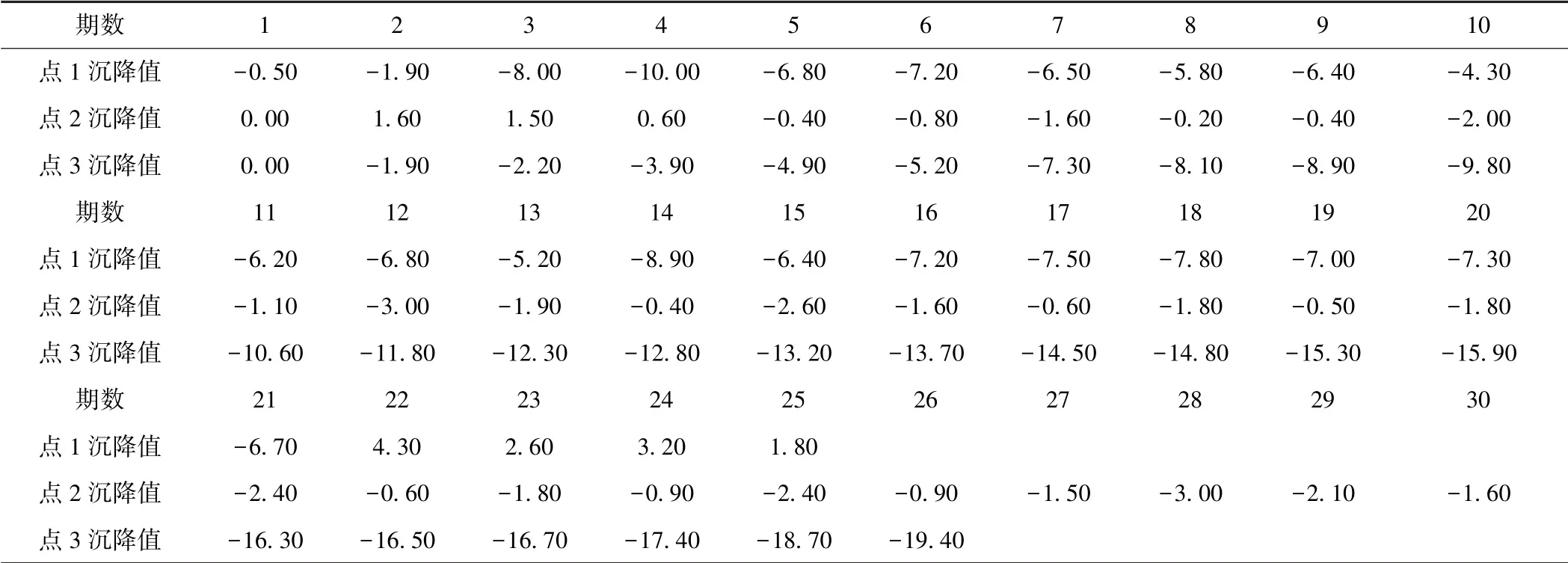
表1 实例数据基本信息 mm

从表1可以看出,监测点1～监测点3沉降数据分别呈现出趋于稳定、来回波动、快速变形的走势,其所在的高铁线路变形监测要求按精密水准测量等级技术执行,水准测量精度为±0.3mm/km,按2.2节对各模型滤波初始参数进行设置。3个监测点的对应的各模型滤波结果见表2～表4;滤波值与监测值的差值见图2～图4;滤波精度评估指数见表5、表6。

图2 监测点1的 Kalman滤波与监测值之差

图4 监测点3的 Kalman滤波与监测值之差

表2 监测点1的Kalman滤波结果 mm

表4 监测点3的Kalman滤波结果 mm

表5 单位权中误差统计 mm

表6 滤波值精度评价 mm

表3 监测点2的Kalman滤波结果 mm

图3 监测点2 的Kalman滤波与监测值之差

由上述图表可知:①常速和加速模型的滤波残差值皆远小于静态模型,两者残差最大值分别为0.749mm、0.0181mm,而静态模型的残差最大为8.28mm;②静态模型的单位权方差σ2最大为 94.0330mm2,而常速和加速模型的最大单位权方差σ2分别只有0.7256mm2,0.3213mm2;③三者的评价指数RMSE、MAE的值呈数量级式变化,静态模型的RMSE、MAE最大值分别为2.5911mm、1.7600mm,常速模型RMSE、MAE最大值分别为0.0536mm、0.0364mm,加速模型RMSE、MAE最大值分别为0.0076mm、0.0066mm。上述评价指标都显示滤波拟合效果排序为:加速模型最优,常速模型次之,静态模型最差。综合而言,Kalman加速滤波模型能更好地拟合变形体变化趋势,滤波值较监测值而言精度更高。

4 结论

运营高速铁路沉降监测数据是动态的,Kalman滤波作为变形监测动态数据分析的常用模型之一,能有效剔除观测数据中的噪声因子,快速改善运营高速铁路沉降监测数据的质量,提高运营高速铁路沉降监测数据的精度。然而,上述卡尔曼滤波模型都是基于固定参数进行设定,当实际噪声不满足白噪声设定时,如何自动改变系统参数设置,以达到自适应的效果,还需要进一步研究。