抗差Kalman滤波算法研究及其在GPS监测数据中的应用

焦雄风 陈 铮 杨兴旺 索广建 张献州

(1.西南交通大学地球科学与环境工程学院,成都 611756; 2.西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,成都 611756; 3.上海铁路北斗测量工程技术有限公司,上海 200071; 4.中国铁路上海局集团有限公司,上海 200071)

1 概述

Kalman滤波在许多领域应用广泛,但受制于其动态系统模型中随机噪声设定(必须为白噪声),对观测手段和环境要求较高。抗差Kalman滤波的提出可有效解决上述问题。赵长胜针对GPS精密定位问题,提出有色噪声作用下的抗差Kalman滤波,并对其公式进行详细推导[1];刘华夏探讨一种抗差自适应Kalman滤波方法,并将其应用于高速铁路变形监测数据的分析中[2];张海平针对BDS-3星座的中长基线实时动态定位,等提出一种基于组合观测值的实时动态(RTK)卡尔曼滤波定位算法,并获得厘米级的定位精度[3-4];贺晗等将抗差Kalman滤波应用于塌陷区监测数据的处理中[5];余航等推导了针对动态EIV模型的总体卡尔曼滤波方法及其近似精度评定公式[6]。

然而,基于不同准则下的抗差Kalman滤波性能差异较大。以下对抗差Kalman滤波、经典Kalman滤波以及小波阈值去噪方法应用于实际GPS单历元解算进行研究,以期获得最优方法。

2 抗差Kalman滤波

2.1 经典Kalman滤波

Kalman滤波是一种能够对包含噪声的观测数据进行降噪处理,从而得到观测目标状态最优估计的算法[7],其离散线性系统下的Kalman滤波基本函数模型方程组由状态方程和观测方程构成,即

式中,xk为(n×1)初始状态参数矩阵;zk为(m×1)测量参数矩阵;wk为(n×1)动态噪声;vk为(m×1)测量噪声;Φk/k-1为(n×n)状态转移矩阵;Hk为(m×n)观测矩阵;Bk/k-1为(n×r)控制参数的增益矩阵;uk-1为(r×1)控制参数矩阵,下标k表示第k时刻。

上述系统的随机模型设定为

式中,Qk为动态噪声wk的非负定方差矩阵;Rk为系统观测噪声vk的正定方差矩阵;δkj为克罗内克函数,即

上述^X可按如下几步公式递推演算得到。

状态值及估计协方差矩阵一步预测为

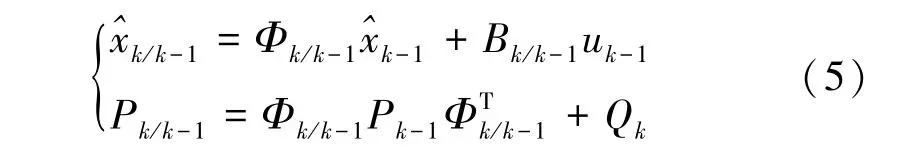
观测噪声协方差及最优卡尔曼增益矩阵一步更新为

更新的状态估及协方差估计为

通过上述公式递推流程,若给定初值状态参数以及在k时刻下的观测值Zk,就能得到在k时刻下目标状态的一步预报值^xk/k-1和估值xk(k=1,2,3,…,N)。

2.2 Huber法抗差Kalman滤波

经典Kalman滤波迭代方式主要由预测加更新的线性回归方式构成,其主要结合观测量和增益矩阵K进行估计[8],可将其构造为

令

由此,卡尔曼滤波迭代式可等价于式(10)的线形回归方程式,而对于求解上述线形回归方程式,可以利用稳健估计中的“M估计”来解决[9],即

式中,εk,i为εk的第i个元素。

通过上述稳健估计方法,可得Kalman更新方程为

2.3 最大相关熵法抗差Kalman滤波

如2.2节推导类似,由经典Kalman滤波迭代公式可以构造得到式(8),再令

式中,K(p)、K(r)是用平方根法对P、R进行分解得到[10],对式(8)同时乘,可得

由此,Kalman滤波迭代式同样可等价于式(13)的线形回归方程式,而对于求解上述线形回归方程式,可以采用如下方法[11],即

式中,N为已知信息个数,c(i)k为Ck的第i个元素,d(i)k为Dk的第i行元素。根据最大相关熵准则可知xk的最优估值为

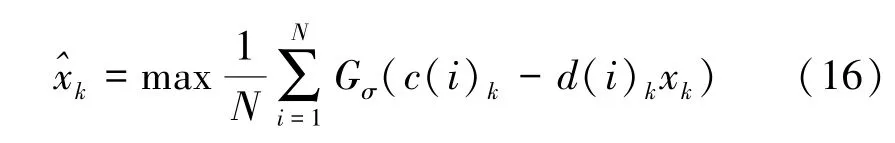
求取上述最优估值等价于求取xk的一个固定解方程,即

求解上述固定解方程,再结合固定解最终形式及经典Kalman滤波的更新方程[12],有

3 精度评价指标

引入均方根误差RMSE(Root Mean Square Error)、平均绝对误差MAE(Mean Absolute Error)、信噪比dB(signal-to-noise ratio)、平滑度r(smoothing of signal)来对滤波去噪效果进行评价[13]。其中,RMSE能反映实际信号与滤波信号之间的偏差,其值越小表明其滤波效果精度越好;MAE能反映滤波信号误差的实际情况,其值越小表明模型拟合程度越高,dB能衡量实际信号和滤波信号的相似度,其值越高表明滤波效果越好;r用来评价滤波信号的整体误差情况,其平滑度越小表明滤波整体误差偏移量越小,具体公式为

式中,n均为采样次数;νk为滤波值与实际值的差值。

4 实例分析

4.1 工程概况

某跨长江公铁两用特大桥全长约10km,位于江苏省境内,其主航道桥段采用双塔三索面箱桁组合梁斜拉桥方案,主跨长约1km,桥上铁路列车设计速度为200km/h,在其主跨段双塔顶端、跨中及东西两侧各设1个GNSS监测点。

4.2 滤波效果比较及精度评价

上述监测点获取的GPS单历元解算数据涉及到监测点位置、变化速度以及时间的计算,这些参数主要受多路径效应、观测值噪声及其他误差源的影响,在上述误差的影响下,可能会导致解算的数据出现较大偏差[14]。一般情况下,偶然误差可以通过经典Kalman滤波以及其他一些去噪方法进行去除,但当误差超出偶然误差的范围时,上述方法就不适用了。而抗差Kalman滤波可以基于稳健估计准则或通过最大化相关熵,对异常粗差进行有效探测及去除,以保证GPS单历元解算数据的准确性[15]。

为比较上述抗差Kalman滤波及经典Kalman滤波效果,选取该桥跨中监测点某个观测时段的GPS单历元解算数据,得到该监测点在北(N)、东(E)方向上的实时位置(de、dn),本次采样个数共3587个,如图1所示。在第100、250、500、900、1300、1800、2900、3300处,人为添加不同数值的粗差,再采用Huber抗差Kalman滤波(HKF)、最大相关熵法抗差Kalman滤波(MKF)、经典Kalman滤波(CKF)进行分析,为测试三者的去噪能力,设置同样的初始参数,状态向量参数设置为位置和速度,初始位置设为不同方向上第一个时间点采样的位置,初始速度设为0,初始估计协方差初始动态噪声的协方差矩阵Q0=初始观测噪声协方差矩阵R0=状态转移矩阵观测向量H=具体滤波结果见图2、图3。

图1 实例数据

由图2、图3可知,在无异常干扰的观测数据处,三者滤波效果基本上都达到优良范围;而在人为添加的粗差处,最大相关熵法抗差Kalman滤波表现出强大的去噪能力,有效排除了异常噪声的干扰,其残差范围控制在厘米级;Huber法抗差Kalman滤波也能探测到部分粗差,但其残差范围仅为分米级;经典Kalman滤波在异常噪声处的去噪效果最差,基本上无法滤掉粗差,其在异常噪声处的残差最大为20m。为进一步对上述抗差Kalman方法的性能进行综合评价,采用小波阈值分析的方法,对上述添加粗差的GPS单历元差分解算数据进行去噪处理。小波阈值也是目前在GPS单历元解算数据去噪方面较为常用的方法[16-17],阈值类型可选择rigrsure(无偏估计),阈值使用方式可为软阈值,且阈值处理不随噪声水平变化而变化,具体处理结果如图4、图5所示。

图2 de滤波结果及残差

图3 dn滤波结果及残差

图4 de小波阈值去噪结果及残差

图5 dn小波阈值去噪结果及残差

由图4、图5可知,小波阈值分析方法只能消弱偶然误差的影响,无法对粗差进行有效探测,达不到有效消除粗差的要求。为进一步定量分析上述几种方法的去噪效果,利用第3节提到的精度指标来评价四者的去噪能力,相关统计数值如表1所示。

表1 三种滤波去噪能力评价指标

由表1可知,最大相关熵法抗差Kalman滤波、Huber抗差Kalman滤波的精度指标总体上优于经典Kalman滤波和小波阈值去噪方法。通过对比,表明最大相关熵法抗差Kalman滤波去噪效果最好,Huber法抗差Kalman滤波次之,经典Kalman滤波和小波阈值去噪效果最差。综合可知,最大相关熵法抗差Kalman滤波能有效探测粗差并改善估值精度,去噪能力为四者中最优。

5 结论

通过对含有粗差的GPS单历元解算数据进行分析,比较最大相关熵法抗差Kalman滤波、Huber法抗差Kalman滤波以及经典Kalman滤波在异常噪声下的去噪效果。实验结果表明,最大相关熵法抗差Kalman滤波具有最优降噪能力。其原因为,最大相关熵法抗差Kalman滤波从估计误差和残差的相关熵方面考虑,通过最大化相关熵来提高状态估计的精度,该方法在异常噪声的干扰下仍然适用;Huber法抗差Kalman滤波利用最小二乘的原理进行估计,这就导致即使观测值为粗差时,仍然会对其赋予一定的权重,从而导致滤波精度下降;经典Kalman滤波也是利用加权平均的思想,但迭代方式决定了其对异常噪声基本上无法有效去除;而小波阈值去噪的核心是根据临界阈值来判断噪声和真实信息,临界阈值则是根据小波系数的大小来设置,而粗差的出现会导致小波系数出现严重的不均匀性,继而可能产生错误的阈值设定,导致去噪效果出现严重下滑。