单自由度复阻尼耗能减震结构的等效系统研究

李创第，谭伟东，葛新广，柏大炼

(1.广西大学 土木建筑工程学院，广西 南宁 530004;2.广西科技大学 土木建筑工程学院，广西 柳州 545006)

0 引言

阻尼是描述结构振动过程中能量耗散的重要参数[1]，如何确定阻尼在结构振动过程中的作用及其效应是振动界较为关注的问题之一。随着人们对阻尼问题研究的不断深入，国内外学者提出了众多不同的阻尼理论，其中以黏性阻尼理论和复阻尼理论为主[2-3]。黏性阻尼理论以其易于数学处理的特性被广泛应用于工程抗震分析中[4]，并且已经发展出了较成熟的计算方法，但黏性阻尼理论存在每周期的能量耗散与激励频率有关的缺陷[5-6]，与大量的固体材料实验现象不符。复阻尼理论是在大量固体材料实验的基础之上总结出来的[7]，具有能量耗散与频率无关的优点，对于大多数工程材料来说，复阻尼理论更易于描述材料的阻尼特性[8]。然而复阻尼理论具有两大缺陷，一是复阻尼结构运动方程在频域求解时需要计算庞大的频率响应函数矩阵[9]，计算工作量过大；二是时域解法的通解中通常包含有发散的分量[10]，当地震持时较长时，复阻尼结构振动方程的时程积分计算不能保证稳定收敛[11-12]，不便于实际工程应用。可见，寻求一种新的阻尼模型用以克服上述两种阻尼理论存在的缺陷有着重要的理论和实际意义。

如何既保证结构能量耗散与外激励频率无关，又能获得时域计算稳定收敛的结果，是当前研究的一个重要方向[13-14]。胡海岩[15]提出了两种复阻尼模型的近似处理方案，一种是对复阻尼系统动响应每一优势频段都用一近似黏性阻尼来等效，另一种是将复阻尼模型近似等效为三参数黏性阻尼模型，但这两种近似模型都对激励频率较为敏感，可能会出现较大误差。何钟怡等[16-17]将复阻尼理论的频域本构推广到时域本构时，为获得时域离散计算的稳定解，使用Maxwell-Kelvin型本构来近似等效复阻尼理论的时域本构。朱镜清[18-19]研究了简谐激励作用下复阻尼运动方程在实数域中的表达形式，提出了频率相关黏性阻尼理论。孙攀旭等[20]在此基础上研究了频率相关阻尼理论的复模态叠加法和时程积分计算，计算结果具有稳定性的优点，但频率相关黏性阻尼理论是在简谐振动激励下的复阻尼振动方程通过频域转化得到的，阻尼力与频率有关，这与结构简谐振动实验中阻尼力在一定频带内定常的现象不符[15]，模糊了阻尼的物理本质。刘庆林等[21]利用Rayleigh阻尼矩阵关于振型正交的特性，构建了基于复阻尼理论的Rayleigh阻尼模型。

复阻尼理论中的结构阻尼损耗因子η较小，且耗能减震结构的动力响应特性完全取决于结构的自振特性[22-26]，基于以上两点性质，本文重构了单自由度复阻尼耗能减震结构的自振方程，利用多尺度方法[27]获得了结构等效频率和等效阻尼比的二阶近似解析式，为今后复阻尼耗能减震结构的高阶等效系统研究打下了基础。

1 运动方程

大量结构的动力性能试验和地震观测结果表明，如果结构作稳态简谐振动，在相当宽的频率范围内结构阻尼力的大小与结构相对位移成正比，相位与振动速度同相[12]，阻尼力在复数域表示为

fd=iηkx，

(1)

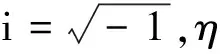
在地震激励作用下，单自由度复阻尼耗能减震结构计算简图如图1所示，由式(1)可知其运动微分方程为

图1 单自由度复阻尼耗能减震结构

(2)

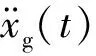
式(2)可简化为

(3)

2 二阶近似等效系统

利用自由振动特性完全相同的等效原则[22-26]，结合多尺度方法对单自由度复阻尼耗能减震结构运动微分方程进行自振特性分析，式(3)的自振方程为

(4)

其中，η为微小量。利用多尺度法进行分析，令η=ε，自振方程(4)可改写为

(5)

继续改写，化为如下两式：

(6)

(7)

式中，ωe为待求等效频率。

自振方程(6)的二阶近似等效系统可表示为

(8)

式中，εc1、ε2c2分别为待定一阶、二阶等效阻尼比。

由多尺度方法[27]可知，为了得到二阶近似解，需要使用3个时间尺度：

T0=t,T1=εt,T2=ε2t，

(9)

则结构的自由振动响应x是以各时间尺度T0、T1、T2为自变量的函数：

x(t)=x0(T0,T1,T2)+εx1(T0,T1,T2)+ε2x2(T0,T1,T2)+o(ε3)，

(10)

此时x不仅依赖于ε和t，还依赖于T0、T1、T2，则x对时间t的各阶求导为

(11)

(12)

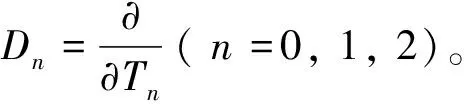
将式(10)至式(12)代入自振方程(6)及其等效系统(8)中，通过比较参数ε的同阶次项系数，可得到一系列线性偏微分方程：

(13)

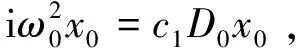
(14)

(15)

其中，式(13)的通解为

x0=A1(T1)A2(T2)eiωeT0+cc，

(16)

式中，A1(T1)、A2(T2)为待求函数；cc表示其前一项的共轭复数项。

将式(16)代入式(14)并化简得

(17)

将式(16)代入式(15)，消除久期项后得

c2=0，

(18)

(19)

由式(7)、式(17)至式(19)可得单自由度复阻尼耗能减震结构的等效频率和等效阻尼比为

(20)

(21)

ε2c2=0，

(22)

式(21)表明等效阻尼比中不包含有外激励频率，与结构简谐振动实验中阻尼力在一定频带内定常的实验现象相符。基于任意激励作用下结构的响应特性完全由其自由振动特性确定的性质[25-26]，可知单自由度复阻尼耗能减震结构的二阶近似等效系统为

(23)

3 等效系统的精度分析

3.1 频率响应函数对比分析

对于单自由度复阻尼耗能减震结构运动微分方程(3)，其频率响应函数为

(24)

对于本文方法求得的等效系统(23)，其频率响应函数为

(25)

目前国内外研究耗能减震结构等效阻尼比的近似方法主要是模态应变能法[28-30]，由模态应变能法得到单自由度复阻尼耗能减震结构的近似等效系统为

(26)

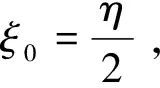
(27)

依据目前实际工程中常见的单自由度结构，结构无阻尼自振频率大约为10～30 rad/s。本文以自振频率ω0=15 rad/s的单自由度复阻尼耗能减震结构为例，结构阻尼损耗因子η分别取0.1,0.2,…,0.8，相应各频率响应函数模曲线如图2至图9所示。

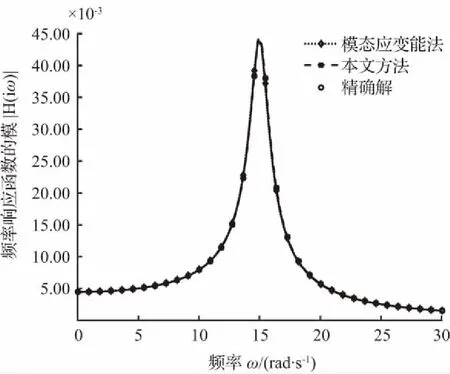
图2 频率响应函数模曲线(η=0.1)

图3 频率响应函数模曲线(η=0.2)

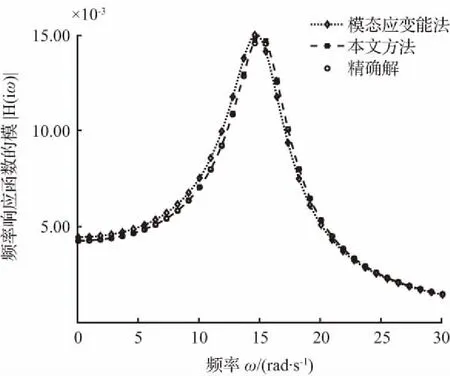
图4 频率响应函数模曲线(η=0.3)

图2至图5表明，结构阻尼损耗因子η从0.1变化至0.4，基本涵盖了实际工程中结构的阻尼损耗因子的变化范围，本文方法与精确解的误差始终保持在2 %以内，而经典模态应变能法与精确解的最大误差已经达到了11.8 %，说明本文所提方法比经典的模态应变能方法精度高。

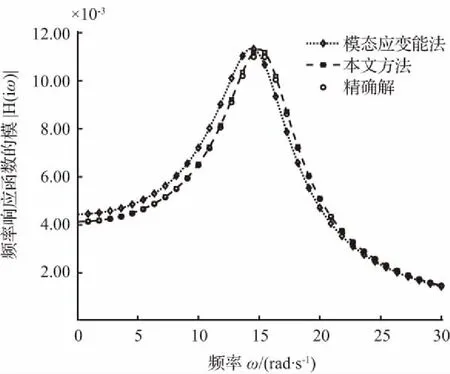
图5 频率响应函数模曲线(η=0.4)

图6至图9表明，随着结构阻尼损耗因子η的增大，本文方法和经典模态应变能法所得等效系统的频率相应函数模曲线都逐渐偏离精确解，但前者的偏离速度明显小于后者，即使η增大到0.8，本文方法与精确解的最大误差只有5.5 %，而经典模态应变能法与精确解的最大误差甚至达到了29.1 %，说明本文方法对于结构阻尼损耗因子的敏感程度低于经典模态应变能法。

图6 频率响应函数模曲线(η=0.5)

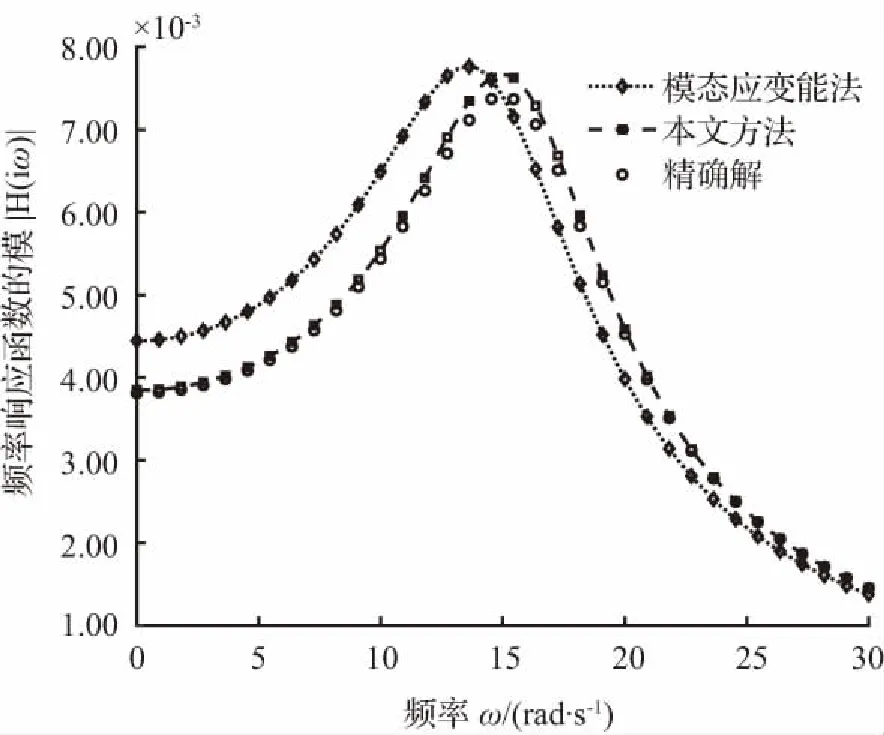
图7 频率响应函数模曲线(η=0.6)

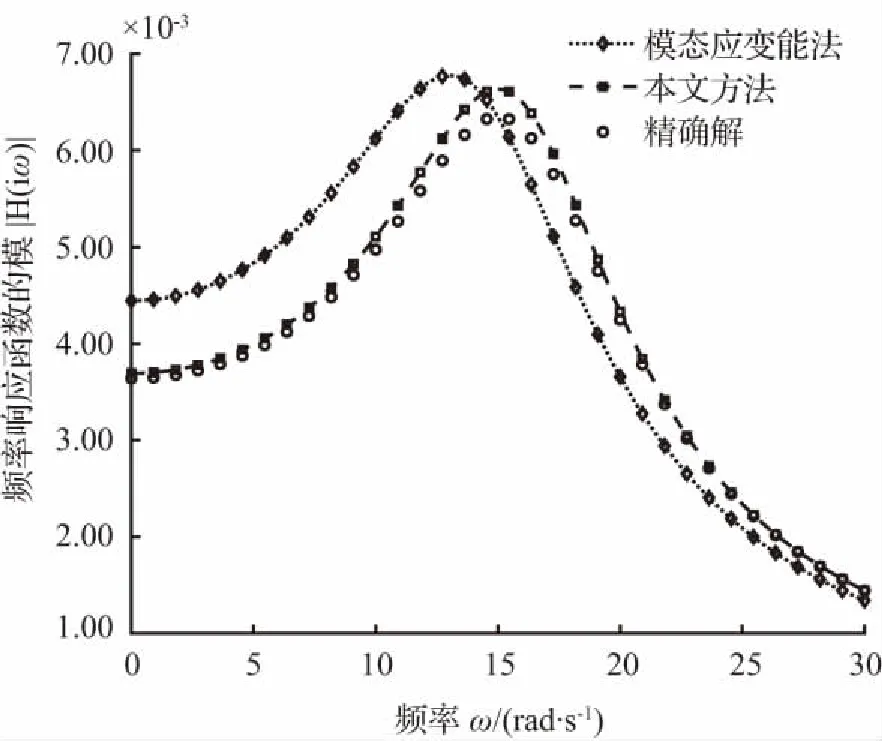
图8 频率响应函数模曲线(η=0.7)

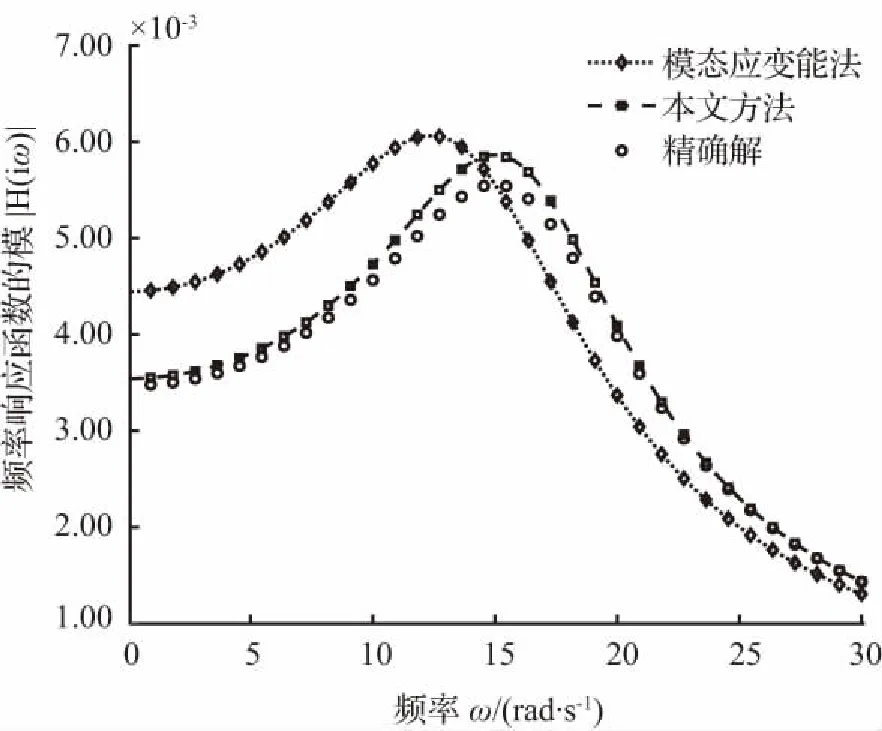
图9 频率响应函数模曲线(η=0.8)

3.2 平稳响应方差对比分析

(28)

原始方程及其近似等效系统的频率响应函数解析表达式已由式(24)、式(25)和式(27)给出，由此可得结构位移平稳响应方程精确解析式为

(29)

由多尺度法求得二阶近似等效系统在平稳白噪声激励下的位移平稳响应方差解析式为

(30)

由模态应变能法所得的位移平稳响应方差解析式为

(31)

以自振频率ω0分别取为15 rad/s、25 rad/s的单自由度复阻尼耗能减震结构为例，功率谱密度取S0=1 m2/s3，在平稳白噪声激励作用下，本文方法和模态应变能方法求得的位移响应方差与精确解的位移响应方差之间的相对误差曲线分别示如图10、图11所示。对于实际工程中的单自由度复阻尼耗能减震结构，在平稳白噪声激励作用下，本文方法计算所获得的位移响应方差精度比模态应变能法有较大提高，当结构阻尼损耗因子η<0.4时，本文方法的误差控制在2 %以内。

图10 响应方差相对误差(ω0=15 rad/s)

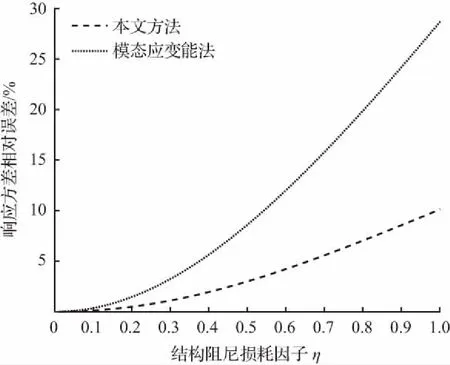
图11 响应方差相对误差(ω0=25 rad/s)

4 地震激励作用下等效系统的响应时程计算

朱敏等[11]已经研究了求解复阻尼结构运动方程的平均常加速度法，本文采用文献[11]的方法计算单自由度复阻尼耗能减震结构在地震激励作用下的响应时程。

对于本文等效系统(23)，采用平均常加速度法计算其动力响应时程，根据平均常加速度法的假定：

(32)

式中,Δt为时间积分步长。由式(32)可得

(33)

(34)

(35)

(36)

将式(35)和式(36)代入t+Δt时刻的式(23)，并从中解出x(t+Δt)：

(37)

式(35)至式(37)即为本文等效系统(23)采用平均常加速度法计算结构动力响应时程的递推公式。

5 算例

依据实际工程中常见的单自由度结构，本文以自振频率为10 rad/s的单自由度复阻尼耗能减震结构为例，结构的损耗因子η=0.1，阻尼比ξ=0.05。分别采用复阻尼模型、本文近似等效系统和黏性阻尼模型结合平均常加速度法进行结构动力响应分析。地震激励采用El Centro地震波南北方向分量，地震持时为T=12 s，时间积分步长为0.02 s。结构的位移、速度和加速度响应时程分别如图12至图14所示。

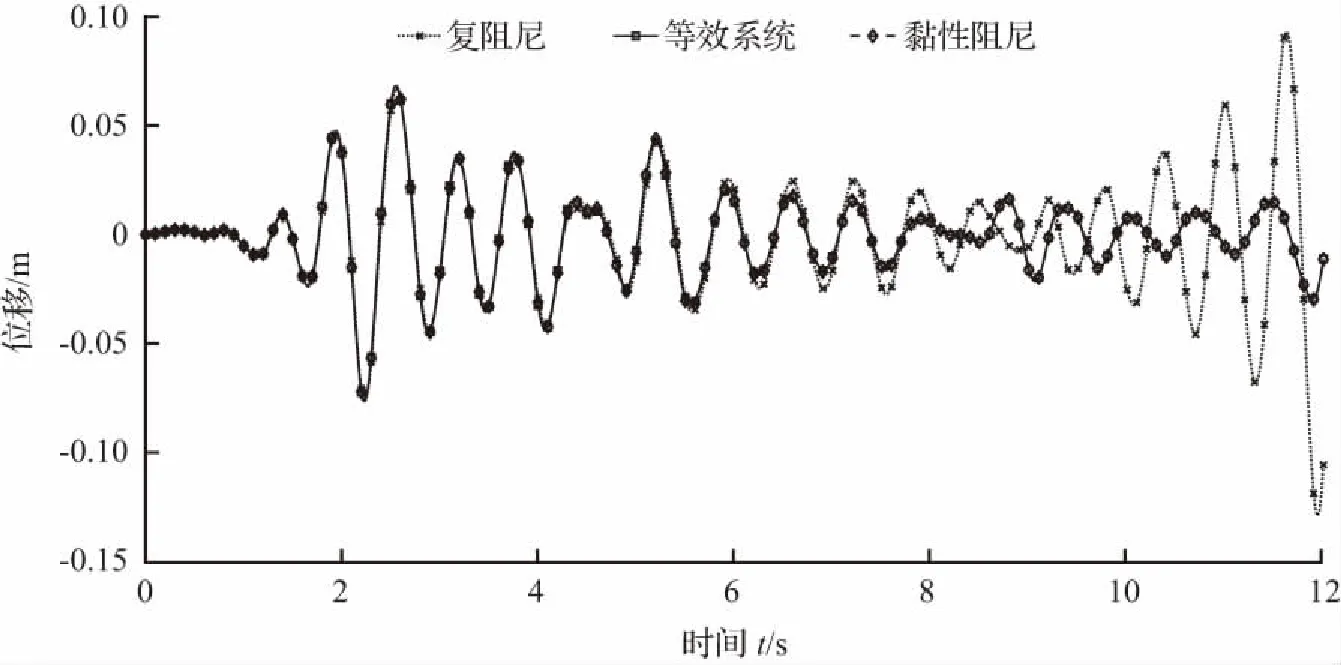
图12 El Centro 地震波南北分量作用下结构位移响应

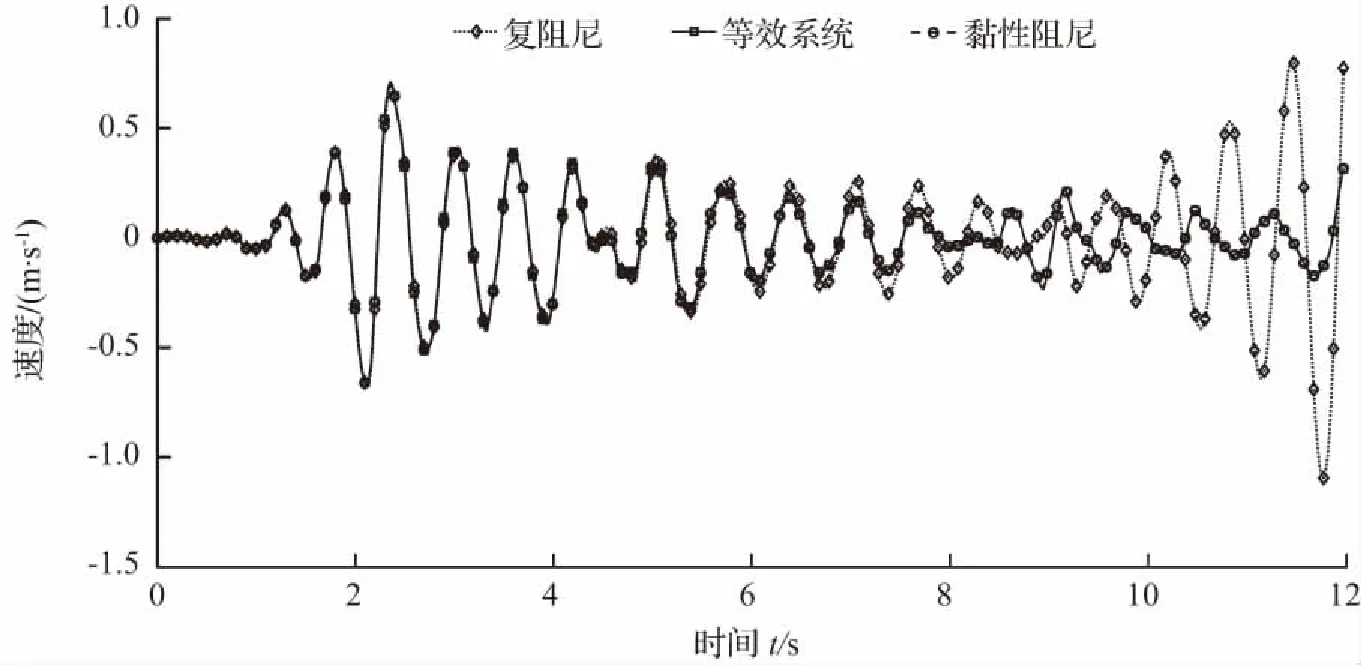
图13 El Centro 地震波南北分量作用下结构速度响应

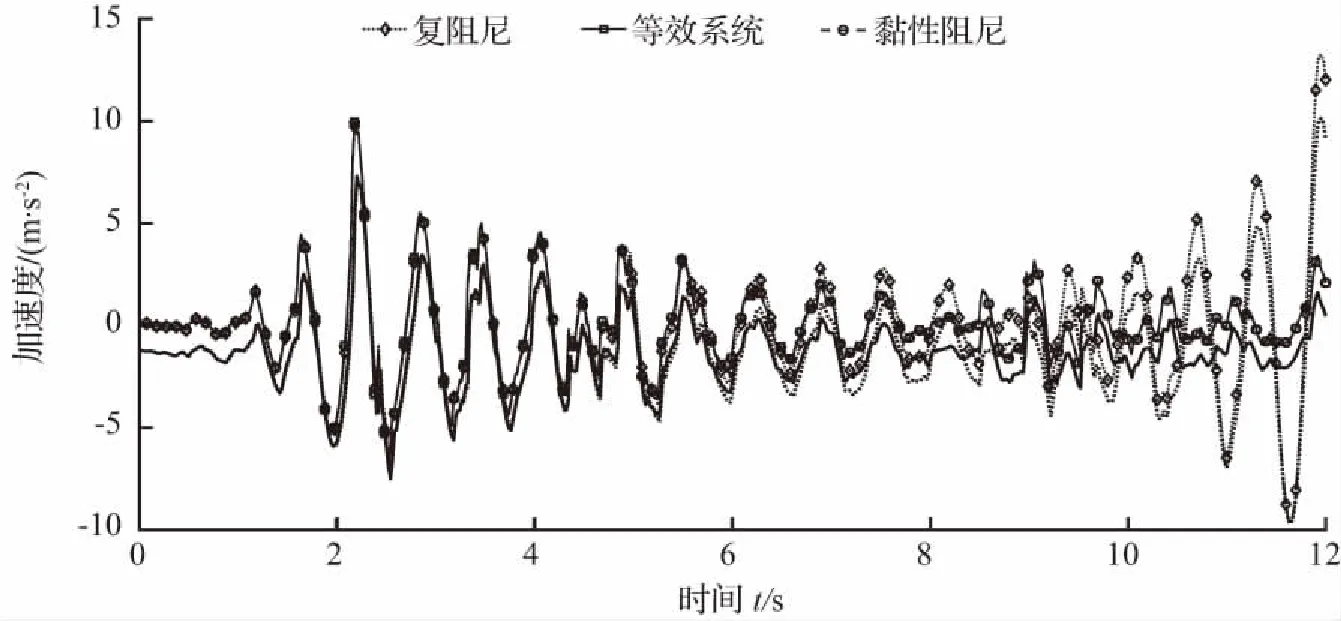
图 14 El Centro 地震波南北分量作用下结构加速度响应

图12至图14表明，当地震作用时间小于7 s时，采用本文等效系统进行动力响应时程分析的计算结果与采用复阻尼模型的计算结果基本保持一致。当地震作用时间大于7 s且小于10 s时，采用复阻尼模型的计算结果出现了不稳定现象。当地震作用时间大于10 s时，采用复阻尼模型计算的位移、速度和加速度响应时程均出现了明显发散现象，因此复阻尼模型只适用于地震持时较小的动力响应时程分析。而本文等效系统与黏性阻尼模型的计算结果近似相等，且在地震持时较大时，位移、速度和加速度的计算结果依然保持稳定收敛。

6 结论

为了克服复阻尼理论的缺陷，研究了单自由度复阻尼耗能减震结构的动力响应，本文基于动力响应特性完全由其自振特性决定的性质和自振方程完全等效的原则，利用多尺度方法获得了单自由度复阻尼耗能减震结构的等效频率和等效阻尼比，并通过算例对比分析了本文等效系统的精度，得到如下结论：

① 频率响应函数和平稳响应方差的对比分析表明，本文方法获得的二阶近似等效系统精度明显优于经典模态应变能法。当结构阻尼损耗因子η≤0.4时，等效系统误差在2 %以内；当0.4<η≤0.8时，等效系统的误差在5.5 %以内，通过增加多尺度法的近似阶数，还可以进一步减小等效系统的误差，对于实际工程具有广阔的应用前景。

② 针对实际工程中的常见单自由度耗能减震结构(10rad/s≤ω0≤30rad/s，0<η<0.4)，相比于经典的模态应变能法，本文方法所建立的二阶近似等效系统的对结构阻尼损耗因子的敏感程度较低。对于大阻尼(η≥0.4)耗能减震结构的动力响应分析中仍然适用。

③ 本文方法建立的单自由度复阻尼耗能减震结构等效系统，结合平均常加速度法，推导了等效系统运动方程逐步积分的递推表达式，算例表明本文等效系统可有效计算出结构的动力响应，并且不受地震激励作用时间的影响，可保证结构动力响应计算结果稳定收敛。