摇臂轴承外圈凸度分析
张 凯,袁祖强,韩 君,高文涛
(南京工业大学 机械与动力工程学院,江苏 南京 211800)
摇臂轴承是发动机配气机构中的一个重要部件,其主要作用是减少配气机构中凸轮与摇臂之间的摩擦,从而改善发动机的工作性能。由于摇臂轴承特殊的工作情况,其整体的受载情况区别于通用圆柱滚子轴承。通用的圆柱滚子轴承通常外圈固定,内圈随轴转动,轴承工作过程中,最大接触载荷以及最大应力往往出现在轴承滚动体上,有数据表明至少有 80%的轴承由于其滚子凸度设计不合理,致使轴承过早失效[1]。因此,国内外学者对滚动体凸度做了大量研究[2-4],并通过对滚动体做了相应的修形改进以提高轴承的使用寿命。而摇臂轴承在实际运动过程中,凸轮带动轴承外圈转动,并且伴有竖直方向的运动,其最大接触应力出现在轴承外圈外表面上[5]。因此,需要轴承的外圈进行修形处理,以提高摇臂轴承的使用寿命。利用ANSYS/LS-DYNA对摇臂轴承进行动力学仿真计算出轴承外圈所受的载荷为3 kN[6],以此作为条件计算摇臂轴承外圈母线在不同形状下的应力变化情况,对比分析进而得到合理的凸形。并以最优凸形为基础计算出最佳的凸度量,从而达到提高摇臂轴承承载能力,改善发动机性能的目的。
1 摇臂轴承外圈母线凸形选择
凸度研究包括对凸度形状和凸度量的研究两块内容,通过一定的经验计算选取合适轮廓线型即凸型设计,凸度量设计即结合轴承外圈所受载荷和轴承外圈宽度,计算出相应凸度值。轴承外圈母线线型设计通常包括如图1所示的几种线型[7]。
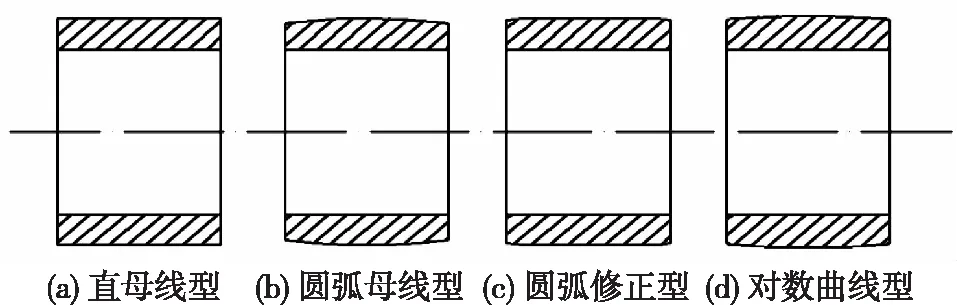
图1 4种不同凸型外圈Fig.1 Four kinds of convex of outer rings
当轴承外圈母线为直线时,可以直接得到。当轴承外圈母线为圆弧全凸线型时,外圈母线线型几何关系如图2(a)所示,凸度量可由式(1)计算得到。当轴承外圈母线为圆弧修正线型时,外圈母线线型几何关系如图2(b)所示,凸度和母线线型计算公式可由式(2)和(3)得到。当轴承外圈母线为对数形状时,外圈母线线型几何关系如图2(c)所示,凸度和母线线型计算公式可由式(4)和(5)得到。
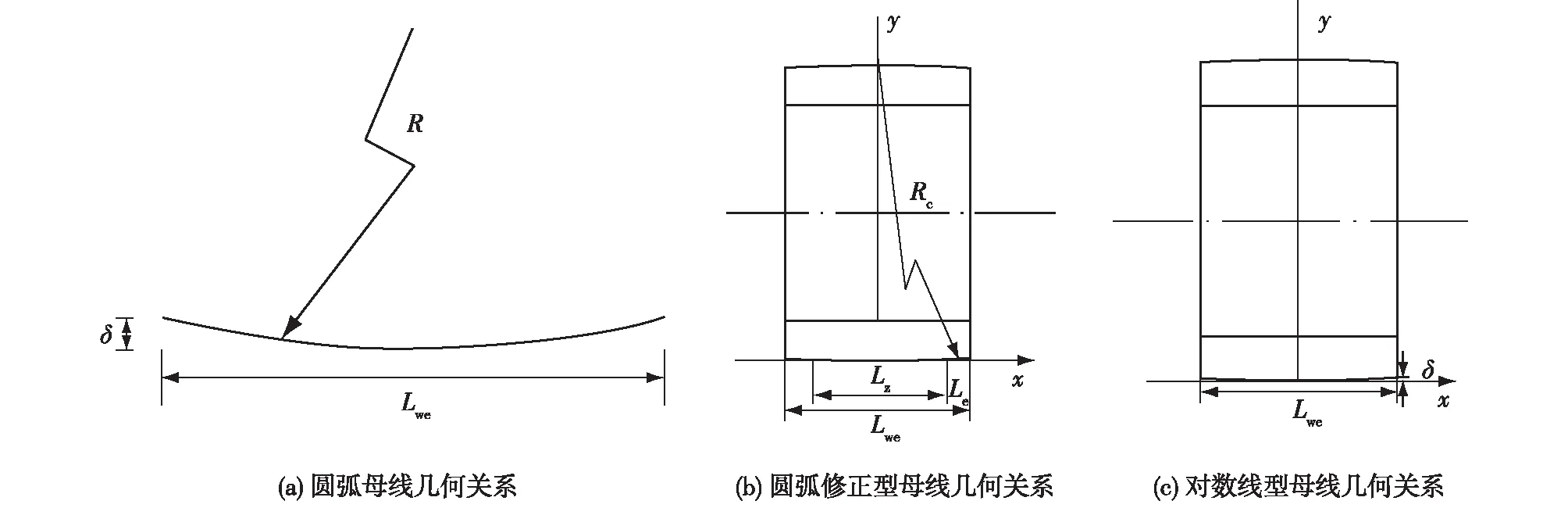
图2 不同外圈母线线型几何关系Fig.2 Geometrical relationship of outer rings with different profiles
(1)
式中:δ1为外圈圆弧母线型对应的凸度量;Lwe为外圈母线宽度;R为圆弧半径。
建立专业协会,通过大户牵头、自愿组合、滚动发展的方式,组织经常性的技术培训、组织申请品牌保护以及开展营销活动等,形成通畅的技术培训和核桃销售渠道。
(2)
(3)
所以算子Γ→C(R,R2)在Bμ(R,R2)中是连续的。类似可证Γ→C(R,R2)在Bμ(R,R2)是连续的。证毕。
根据凸轮与摇臂轴承实体模型可知,其结构在某种程度上成对称分布。为了减少分析中的接触对和节省计算时间,提高工作效率,建立轴承进行模型简化,由于凸轮实际结构比较复杂,对其使用四分之一基圆代替。本章重点分析凸轮与轴承在静力作用下凸度对轴承表面的接触应力的影响,由凸轮与轴承的受力特点可知,在径向载荷作用下,凸轮与轴承接触面处的载荷作用最大,并且该处发生的变形也最大,取轴承实体模型的 1/4为有限元分析模型,简化模型如图4(a)所示。
(4)
(5)
式中:δ3为外圈对数曲线型对应的凸度量;K0为材料常数,轴承钢K0为2.81×106mm2/N;b为凸轮与轴承接触宽度;y2为对数曲线方程;μ为轴承钢泊松比;E为轴承钢的弹性模量。
施工方案模拟时添加时间维度即为4D施工进度模拟,施工模拟采用Navisworks平台,工具Time Liner可添加计划模拟,也可以从各种进度软件中导入进度计划,将进度计划与模型相关联,模拟施工进度。施工模拟既可对整个施工方案进行模拟,研究装配式结构的吊装方案,也可对局部的重点复杂部位进行模拟,模拟其施工安装过程,实现智能施工安装。
2 有限元模型的建立
2.1 实体模型的建立
在ANSYS中采用自底向上的方法建立有限元模型,直线型外圈母线由于线型比较简单可以在ANSYS中直接建立,而圆弧型、圆弧修正型以及对数型外圈母线建立时,根据轴承的受力情况得到其凸度值相对较小,在ANSYS直接得到曲线有困难,因此通过建立若干个点,利用样条曲线的方式来模拟对应的凸度部分。即根据凸度曲线方程拟合出一系列的离散点,通过样条曲线连接得到所要的凸度曲线。在ANSYS中生成的不同凸型曲线的点分别如图3所示。

表1 摇臂轴承尺寸参数表Table 1 Parameters of tappet roller bearing
以常州某轴承公司提供的摇臂轴承为研究对象,轴承的尺寸参数如表1所示,凸轮与摇臂轴承材料均为GCr15。

图3 曲线关键点Fig.3 Key points of the profiles
(3)If Michael had spent more time with his fathere,he would not have lost him with so much sorrow.
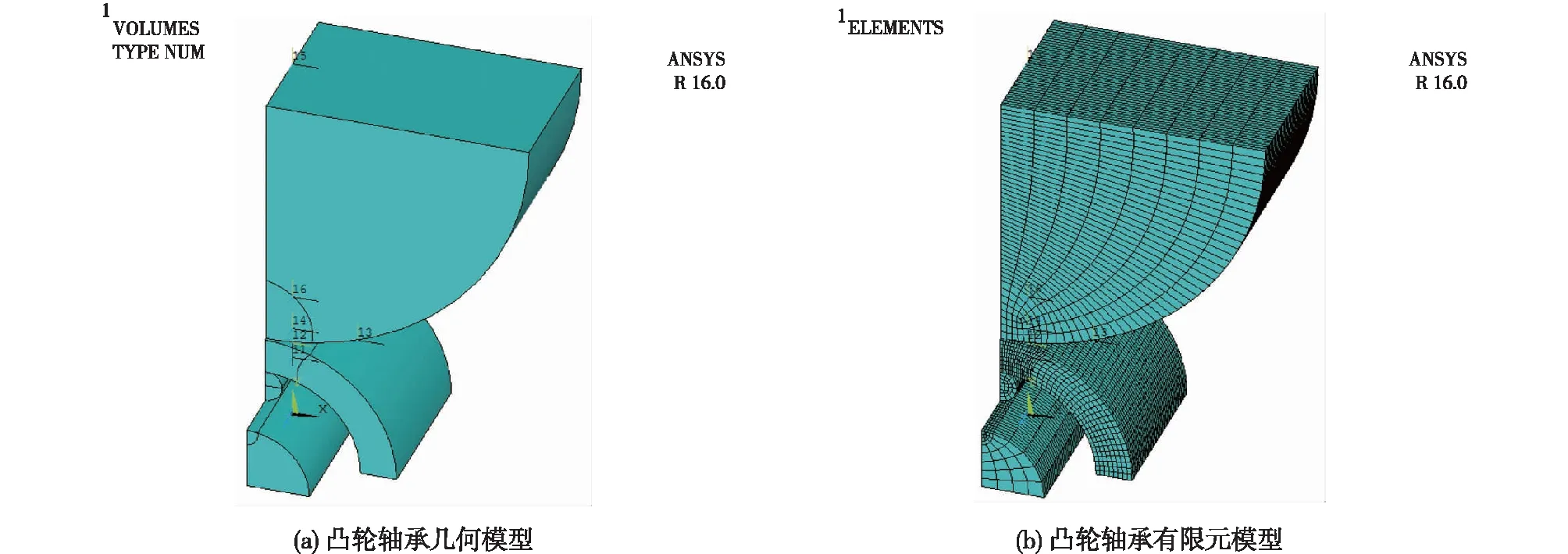
图4 凸轮与轴承简化模型Fig.4 Simplified model of cam and bearing
2.2 材料属性设置及网格划分及接触对设置
通过以上分析可知,轴承外圈母线最优的凸度形状为对数母线型,因此在对数母线线型基础上,考虑凸度量与对应力值变化的关系[11-12]。因为凸度量的大小受到载荷的影响,研究某一特定载荷下其所对应的最优凸度量,当凸轮与轴承接触的平均载荷约为3 kN,采用对数线型母线,对应的对数方程y2见式(6),对应的凸度值如式(7)所示。
式中:δ2为圆弧修正型对应的凸度量;Fr为轴承所受的径向载荷;Lz为母线中间直线长度;Rc为母线圆弧半径;y1为圆弧部分的方程。
2.3 边界条件的设定及载荷
通过以上对摇臂轴承ANSYS前处理工作,求解得到不同凸形情况下摇臂轴承外圈表面应力变化如图5~8所示。图5(a)~图8(a)为轴承外圈表面应力云图,图5(b)~图8(b)为外圈表面应力沿母线路径分布曲线。从图5(a)~图8(a)中可以发现,凸轮与摇臂轴承接触过程中,轴承所受的最大接触应力出现在轴承外圈外表面上,这也说明了对外圈母线修形的合理性。当轴承外圈母线为直母线时,外圈表面应力如图5所示,结合图5(a)、5(b)可以发现,轴承外圈外表面两端应力大,中间应力小,这种现象被称为“边缘效应”[9-10],最大应力达到224.9 MPa。在实际工作中,凸轮与轴承接触如果出现偏载,“边缘效应”会加剧,从而造成轴承过早失效。当轴承外圈线型为圆弧全凸线型时,接触应力分布见图6,从图6中可以发现,最大应力出现在母线中部约为193.9 MPa。这种情况的接触类似于点面接触,实际工作中极易造成偏载,出现应力集中。当外圈母线线型为圆弧修正线型时,外圈表面应力变化见图7,由图7可以看出,凸轮与轴承工作过程中外圈表面最大接触应力出现在母线圆弧与直线过度的地方,最大应力值为171.9 MPa。当外圈母线线型为对数母线线型时,应力分布见图8,从图8中可以发现,轴承外圈表面应力分布较为均匀,“边缘效应”消失,应力最大值为146.3 MPa。通过对比在相同载荷作用下,4种母线线型所对应的应力分布情况可以直观地发现,对数母线线型最优,不仅不会出现应力集中现象,而且所对应的最大载荷也有所减小,因此对数母线线型是最优的线型。
3 轴承外圈凸度有限元分析
3.1 轴承外圈应力场分析
结合模型受力和边界条件进行分析,在竖直分割面上施加X方向对称约束,在销轴的水平分割面上施加Y向约束,在凸轮轴承的侧面施加Z向位移约束,对外圈和滚动体侧面施加周向约束,轴承在工作过程中收到的径向载荷源于凸轮旋转冲击[6],取其平均载荷施加在凸轮上。
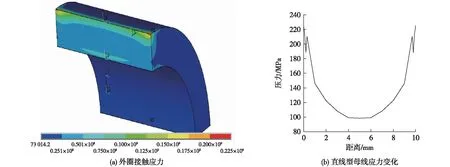
图5 直母线外圈对应的应力变化Fig.5 Stress distributions on the outer rings of the straight profile
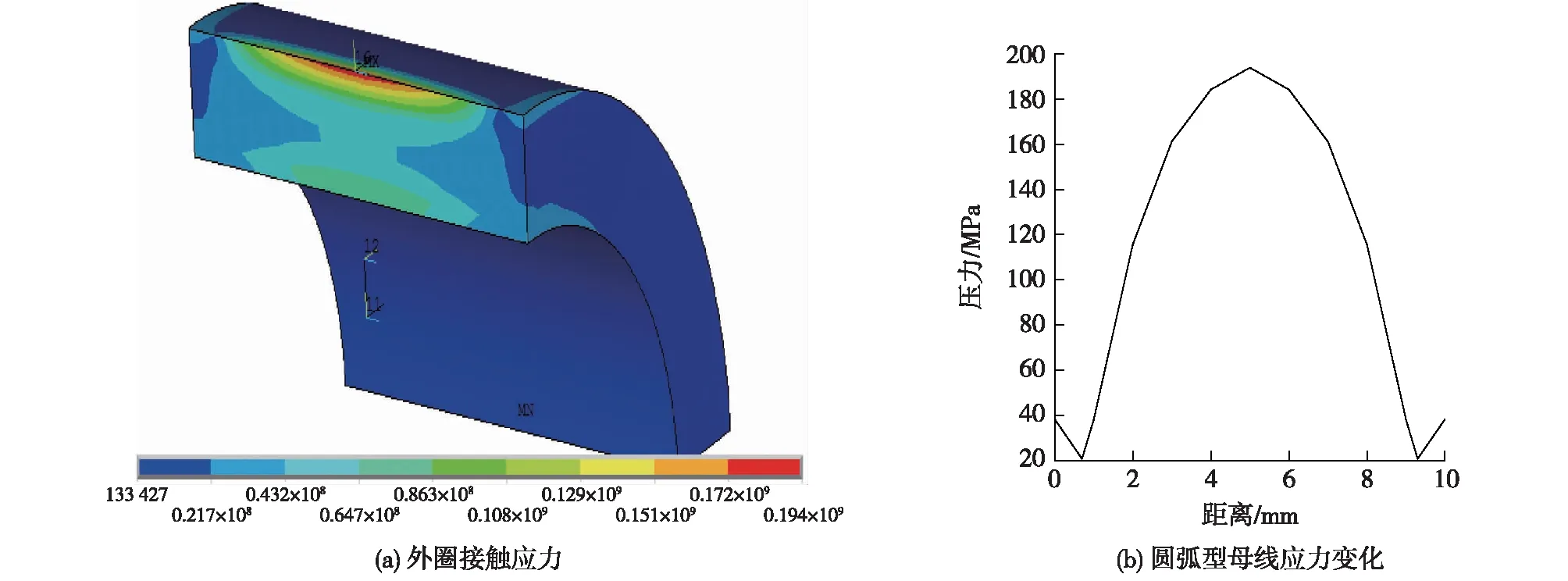
图6 圆弧型母线外圈应力变化Fig.6 Stress distributions on the outer rings of the arc-shaped profile
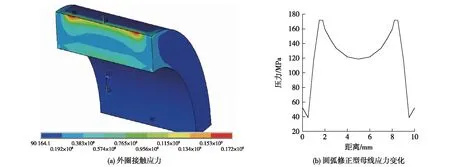
图7 圆弧修正母线外圈应力变化Fig.7 Stress distributions on the outer rings of the arc correction profile
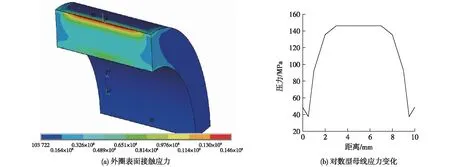
图8 对数型母线外圈应力变化Fig.8 Stress distributions on the outer rings of the logarithmic profile
3.2 外圈母线的凸度量计算
凸轮与摇臂轴承结构采用的材料均为GCr15,部分材料属性参数均在表1中给出。采用8节点185实体单元,在凸轮和摇臂轴承各部件的接触分析过程中,网格划分的合理性,对计算的精度以及求解的时间都有重要影响,划分时对接触的部分进行细化,以提高计算精度,对于非接触的部分,采用粗网格,节省计算时间。采用映射分网与扫掠分网相结合对凸轮与轴承模型进行网格划分,划分完成后共生成36 691个节点、30 592个单元,有限元模型如图4(b)所示。根据接触设置准则,该模型结构共存在3个接触对。设置相应的单元类型,采用接触向导进行接触对设置,设置摩擦系数设定为0.15,接触方式为非对称接触,穿透容差取默认值[8]。
(6)
(7)
根据公式(7)计算得到轴承外圈凸度为4.346 μm,为了得到外圈的最佳凸度值,利用ANSYS对轴承凸度量进行大量研究,控制载荷不变,即保证对数方程不变,通过微调凸度量值的大小,找到最合适的凸度区间,计算结果见表2。从表2中可以发现,载荷为3 kN对应的最优凸度约为7 μm,这与公式计算出来的4.346 μm凸度量有差距,但也不可否认经验公式的合理性。综合以上判断分析得出,当载荷为3 kN时,凸度范围为6 ~9 μm较为合理。
通过计算得出,小传动比钻机绞车减速箱所采用的斜齿轮各个参数为小齿轮齿数31,大齿轮齿数112,螺旋角14.08°,模数7。
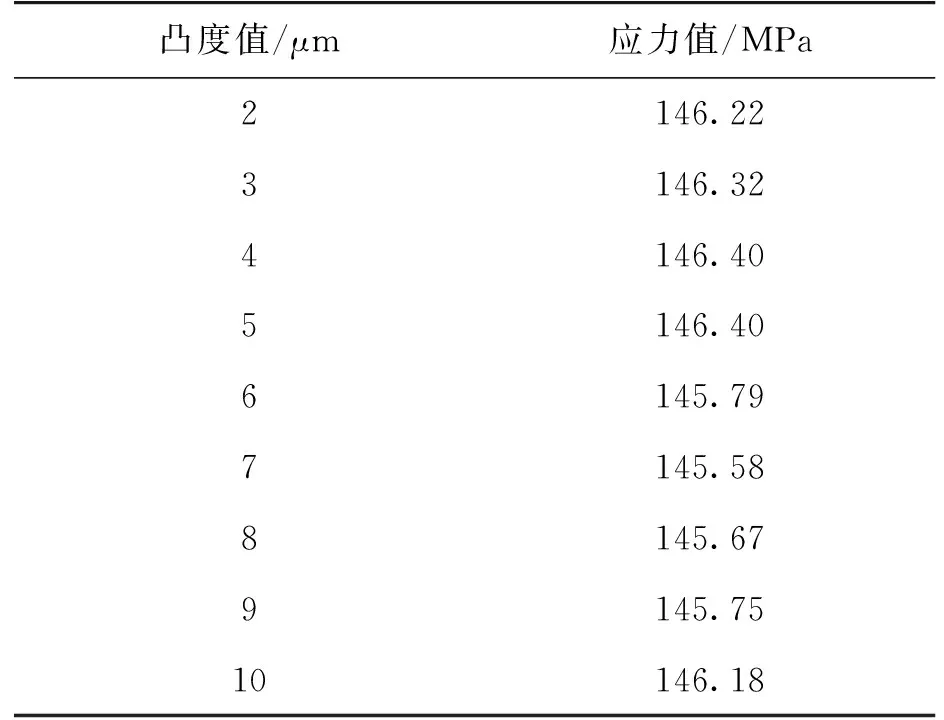
表2 同一载荷不同凸度量下的接触应力Table 2 Contact stresses under the same load with different crowns
4 结论
1)当轴承外圈母线为直母线时,存在明显的“边缘效应”,即最大应力出现在外圈端部;当外圈母线为圆弧全凸型母线时,轴承外圈中部应力最大;当轴承外圈母线为圆弧修正母线时,尽管边缘效应有所改善,但是在母线圆弧与直线过度的地方仍然有应力集中;当轴承外圈母线为对数线型时,边缘效应消失,应力沿母线均匀分布,并且相对于其他母线线型,应力最小。因此,摇臂轴承外圈的最优母线线型为对数线型。
2)轴承外圈凸度量与轴承所受载荷有关,间接地与发动机转速有关。当摇臂轴承所受平均载荷为3 kN、轴承外圈母线为对数母线时,所对应的最佳凸度量为6 ~9 μm,在此范围内的应力分布较小。

