基于频域分析与统计计算的自动睡眠分期研究

陈涛

（佛山职业技术学院，广州佛山，528000）

0 引言

睡眠是一项非常重要的生理活动。人类有1/3 的时间是在睡眠中度过。睡眠质量与身心健康有着密切的关联。好的睡眠质量有助于放松大脑，缓解疲劳，促进健康；反之则容易造成倦怠乏力，注意力不集中，严重者可引发焦躁、抑郁等疾病，损害身心健康[1]。研究表明，睡眠质量的改善可以通过在特定的睡眠时期施加适当的外界干预实现[2-3]。因此，正确识别睡眠时期具有重要的意义。

依照Rechtschaffe 和Kales（简称R&K）分期准则，睡眠过程分为清醒期（Wakefulness,W）、非快速眼动期（Non-Rapid Eye Movement，NREM）和快速眼动期（Rapid Eye Movement，REM）[4]。其中，NREM 期可具体划分为非快速眼动1 期（N1），非快速眼动2 期（N2），非快速眼动3 期（N3）和非快速眼动4 期（N4）。2007 年，美国睡眠医学会（AASM）对R&K 睡眠分期准则进行修订，将N1 期和N2 期整合为浅睡期（Light Sleep，LS）,N3 期和N4 期整合为深睡期（Slow Wave Sleep，SWS）[5]。本文遵照AASM 的睡眠分期标准。睡眠分期结构图如图1 所示。

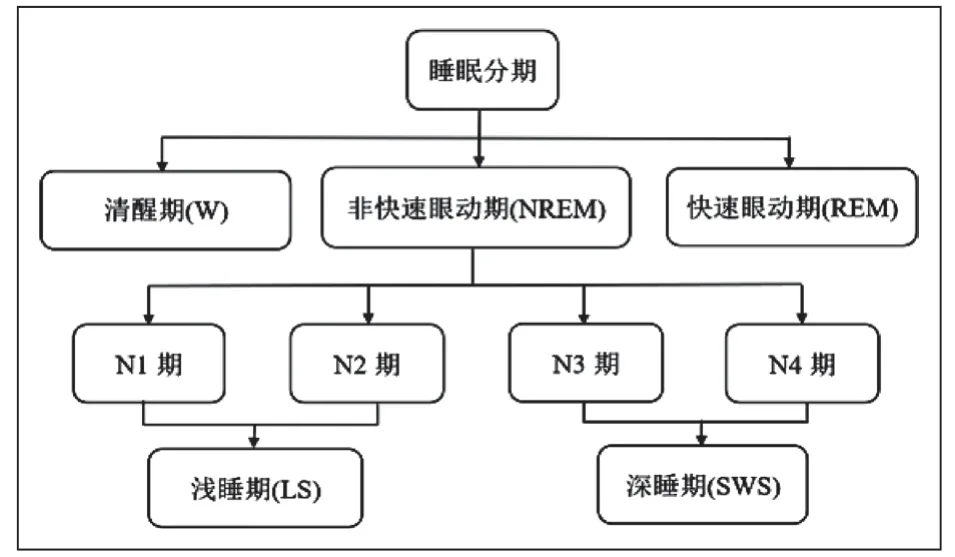
图1 睡眠分期结构图

传统的睡眠分期依靠睡眠专家标定实现。健康成年人整晚的睡眠时间为7～8h，相应的标定工作需要2～4 h，耗时久，工作量大，而且不同睡眠专家的判读结果常存在出入，无法保证一致性。因此，发展自动睡眠分期算法具有重要的意义。

现阶段，睡眠分期研究已经取得了一定的进展。Liang等[6]研究20 位受试者的睡眠脑电（Elect roencephalogram，EEG）信号,提取多尺度熵（Multiscale Entropy）、自回归模型（Autoregressive Model）作为特征，使用线性判别分类器（Linear Discriminant Analysis）对睡眠阶段5 分类，准确率76.91%；Rodriguez 等[7]研究39 位受试者的睡眠EEG 信号，提取分形维数(Fractal Dimension，FD)、去趋势流动分析(Detrended Fluctuation Analysi，DFA)、香农熵(Shannon entropy，H)、近似熵(Approximate entrop，ApEn)、样本熵(Sample Entrop，SampEn)以及多尺度熵(Multiscale Entropy,MSE)等特征，基于K-均值聚类算法对睡眠阶段5 分类，准确率76.8%；Liang 等[8]研究4 位受试者的睡眠EEG 信号，提取功率谱（Power Spectrum），功率比（Power Ratio），谱频率（Spectral Frequency）和时间比率（Duration Ratio）作为特征，使用带有平滑规则的决策树（Decision Tree）分类器对睡眠阶段5 分类,准确率77.98%；Fraiwan[9]等研究16 位受试者的睡眠EEG 信号，应用Choi-Williams 分布提取Delta、Theta、Alpha 等节律波的能量谱特征，结合随机森林分类器对睡眠阶段5 分类，准确率78%；Flexer[10]等研究40 位受试者的睡眠EEG 信号，利用隐马尔科夫模型(Hidden Markov Model，HMM)对睡眠阶段3 分类，准确率接近80%。

本文提出了基于频域分析与统计计算的自动睡眠分期算法。应用小波变换对原始脑电信号进行去噪，傅里叶变换提取频谱特征，统计分析提取均值等特征，运用支持向量机（Support Vector Machine,SVM）对复合特征进行分类识别，达到了快速准确的分期效果。

1 算法描述

■1.1 实验数据获取

本文的睡眠脑电（Electroencephalogram，EEG）信号数据来自美国麻省理工大学BIH 生理信息库中的Sleep-EDF 数据库[11]。选择10 位健康成年人作为研究对象，年龄21 − 35岁，无病史。睡眠脑电数据统一标识格式为SC4ssnE0，其中ss 对应对象标号（0 ≤ ss ≤ 82）；n对应记录的夜晚标号（1 或2）。数据采样频率100Hz，波幅单位µV，记录时长20h，参考导联Fpz−Cz、Pz−Oz。睡眠分期结果已由专家人工标注。

■1.2 特征提取及分类

1.2.1 EEG 信号预处理

由于睡眠EEG 信号极其微弱，容易受到眼电（Electrooculogram,EOG）、肌电（Electromyogram,EMG）等噪声信号的干扰，因此需要对原始的EEG 信号进行去噪预处理。小波变换是在傅里叶变换的基础上发展起来的一种时频域分析方法，在处理非平稳信号方面，具有良好的时频特性，广泛应用于脑电信号的处理[12,13]。

通过实验对比，当使用db4 小波基，分解层数为7，依据无偏风险阈值估计准则（Rigrsure regulation）筛选小波系数时，EEG 信号的高频和低频信息保留最为完整，去噪效果最理想。图2 是依据上述方法对30 s EEG 信号去噪后的结果。

图2 原始EEG 信号和降噪后EEG 信号波形图

1.2.2 频谱特征提取

频谱能量特征是EEG 信号中的重要特征参数。小波变换，傅里叶变换、Hilbert-Huang 变换，Wingner-Ville 分布以及Choi-Williams 分布等都是典型的EEG 信号频谱能量分析方法。本文以傅里叶变换为基础，提取睡眠EEG 信号能量特征[14]。

(1)频谱中心值（Spectral centroid,Sc）

(2)频谱宽度值（Spectral width,Sw）

(3)频谱不对称值（Spectral asymmetry,Sa）

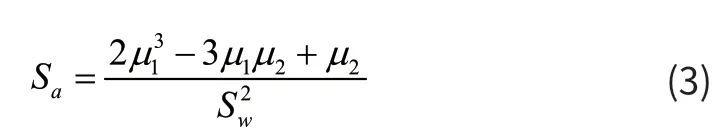
(4)频谱平坦度值（Spectral flatness,Sk）

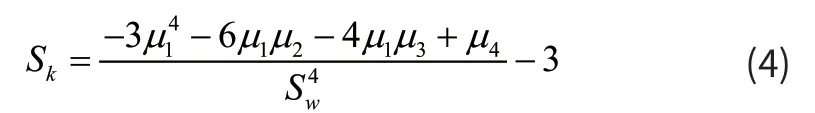
(5)频谱平坦度值（Spectrum flatness,SF）

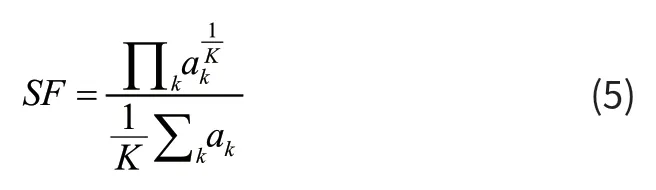
(6)频谱斜率（Spectral slop,Ss）

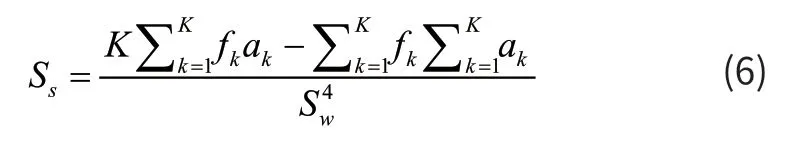
(7)频谱衰减率（Spectral decrease,Sd）

ak代表信号做傅里叶变换后，的频率值对应的频谱幅值。

1.2.3 统计分析特征提取

研究表明睡眠EEG 信号是一种时变的、有源的、非平稳的复杂的非线性动力学信号，可以结合统计分析方法，提取均值、方差以及信号的高阶矩等统计特征[15]，反映睡眠的变化过程，实现睡眠分期。

(1)原始信号平均值

(2)原始信号标准差

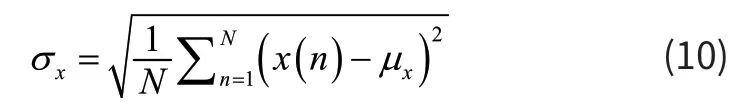
（3）原始信号一阶导数绝对值的平均值

（4）标准化后信号一阶导数绝对值的平均值

（5）原始信号二阶导数绝对值的平均值

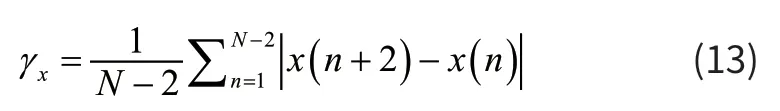
（6）标准化后信号二阶导数绝对值的平均值

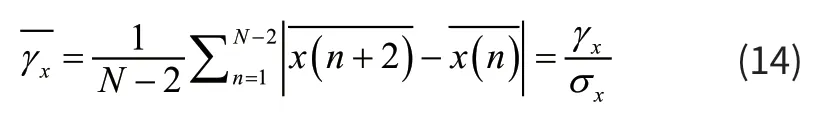
其中，x(n),n=1,…,N代表具有N 个数据点的去噪后的睡眠EEG 信号。

1.2.4 支持向量机分类

支持向量机(Support Vector Machine,SVM)是一种线性判别分类器，通过找到最优超平面，实现样本的正确分类，同时满足样本间的分类间隔达到最大，在脑电信号处理领域得到了广泛的应用[16,17]。

本文选用线性核函数构造分类器，n 倍交叉验证法计算分类准确率。首先将所有的样本进行n 等分，以其中的1份样本作为测试数据集，利用其余的n-1 份样本训练得到的分类器对其进行测试，得到单次实验的准确率。顺次抽取测试数据集，得到n 个准确率。对准确率求平均，以平均值作为交叉验证准确率。同时，为进一步提高准确率的可信度，上述过程可重复k 轮进行。以k 轮的均值准确率作为最终结果。算法过程如图3 所示。

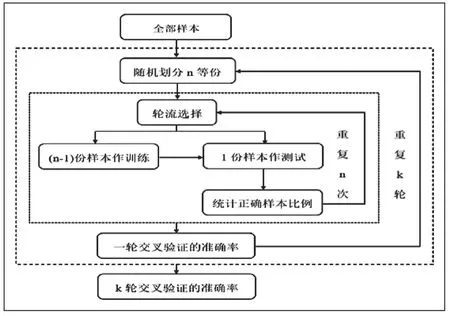
图3 k 轮n 倍交叉验证法示意图

2 实验结果与分析

■ 2.1 睡眠分期结果

本文分别利用Sleep-EDF数据库中的Fpz−Cz、Pz−Oz 通道的睡眠EEG 信号进行实验。前者，平均准确率达到86.82%，卡帕系数0.83；后者，平均准确率达到86.01%，卡帕系数0.81。就单个睡眠时期分类准确率而言，两个实验中，清醒期和深睡期的分类准确率都超过90%。实验结果验证了本文算法的有效性和可靠性。

表1 Fpz −Cz通道准确率与卡帕系数

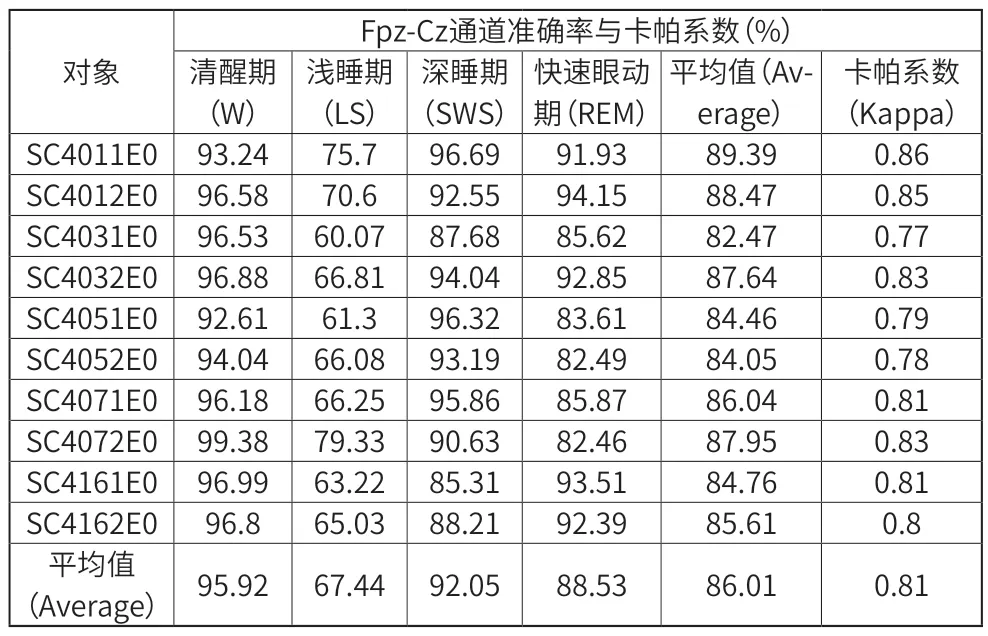
表2 Pz −Oz通道准确率与卡帕系数

■2.2 睡眠分期方法比较

将本文算法同文献[18-21]中的算法进行比较，结果如表3 所示。由表3 可见，与文献[18-21]中的算法相比，本文算法的准确率更高，算法结构也更为简单。

表3 不同算法的分类准确率比较

3 结语

本文提出了一种基于频谱能量值与统计分析的自动睡眠分期算法。使用db4 小波对EEG 信号去噪，傅里叶变换提取频谱能量值特征，统计分析提取均值等特征，支持向量机分类，准确率达到86.82%，验证了本文算法对睡眠分期的可行性和有效性。

本文的研究只是基于EEG。在今后的研究中，还应将其他的生物电信号引入睡眠分期的研究中，如EOG、EMG，进一步提升算法的分类准确率。