基于模糊数学原理的大宗商品质量评判方法

李艳秋 毛成涛 封亚辉 李德军 姜兆兴 姜辉

（1.青岛海关技术中心，山东青岛，266002；2.南京海关工业产品检测中心；3.合肥海关技术中心铜原料及产品检测实验室；4.内蒙古中普检验检测有限公司；5.山东省青岛生态环境监测中心）

1 前言

对于钢铁、有色金属、煤炭等大宗商品，常规质量评判方法是核查其质量指标的实测数据是否符合公认标准或技术协议的要求，只有其质量指标的实测数据全部符合要求，才能判定为合格，否则就判定为不合格。从数学角度来说，这种常规质量判定方法是基于经典集合论的{0，1}模型，这种模型的特征函数只能取值0或1，也只能表达“非此即彼”的现象[1]。

然而，在对大宗商品进行质量评判的实际操作中，却往往会出现“亦此亦彼”的问题，例如：某铅锭的化学成分按照GB/T 469-2013[2]进行检测后，Ni含量为0.0003%（Pb99.994牌号铅锭的Ni含量不得>0.0002%），其他元素均符合Pb99.994牌号的要求，如果按照常规质量评判方法，该铅锭应判定为Pb99.985牌号的级别，但在实际质量管控中，因其Ni含量超出Pb99.994牌号的限值极少而其他元素含量又符合该牌号的要求，往往将该铅锭判定为Pb99.994牌号级别并用于生产制造。显然，使用常规质量评判方法进行此类情况的质量判定缺乏足够的合理性和实用性，也容易造成降级评判和使用浪费。因此，为了解决常规质量评判方法存在的过严评判或无法评判的问题，本文以铅锭的质量评判为例，针对大宗商品提出了基于模糊数学原理的质量评判方法（简称“模糊评判法”），使其既能体现和权衡大宗商品质量指标的符合程度，又能确保判定结论更加符合客观实际和生产需要。

2 模糊评判法的数学原理和应用模型

2.1 模糊数学原理

美国控制论专家查德将经典集合论中特征函数的取值范围由{0，1}推广到闭区间[0，1]，提出了基于模糊数学原理的模糊集（F集）[1]。F集最突出的特点就是其“隶属度”函数和矩阵能更贴切、更客观地反映数据对象之间的相似性和关联性[3]，不仅涵盖和拓展了经典集合论的理论和应用，还为解决“亦此亦彼”的问题提供了适用的原理和方法。

模糊评判法能对受多个因素制约的事物做出全面地评价[4]。在大宗商品（以铅锭为例）的质量评判时，实测化学成分与质量往往会出现“亦此亦彼”性（即：模糊性）：实测铅含量为99.993%的A铅锭的质量非常接近Pb99.994牌号的等级品，却比Pb99.990牌号级别的要求高很多；实测B铅锭的铅含量虽然符合Pb99.994牌号的要求，但其一种或多种杂质元素的实测含量却不符合Pb99.994牌号的要求，如果按照常规质量评判方法，A和B铅锭都只能判定属于Pb99.990牌号及以下的等级品。而F集的隶属函数却能恰如其分地表达和计算出铅锭的每个质量指标实测值与各个牌号限值的接近程度，并根据合理的权重判定其综合质量与各牌号的符合程度。

模糊评判法的评判模型应遵循“择近原则”并选用适当的“贴进度”类型建立隶属函数。“贴进度”是对2个F集接近程度的一种度量。就大宗商品而言，就是其质量指标的实测值与各个牌号限值的接近程度。“择近原则”就通过评判模型计算总体质量与各个质量等级接近程度的量化结果，将总体质量判定为最大量化结果所对应的质量等级。

2.2 模糊评判法的应用模型

2.2.1确定评判数集

模糊评判法首先需要确定评判规则集（质量等级集）、质量指标集（质量因子集）及其权重集。

设v1，v2，…，vn是质量评判所依据的n个质量等级的限值（来源于评判标准或技术协议），则质量等级集V={v1，v2，…，vn}；设u1，u2，…，un为参与质量评判的m个质量因子，则质量因子集U={u1，u2，…，un}；设a1，a2，…，an是分别是质量因子u1，u2，…，un影响总体质量的权重数，则权重集A={a1，a2，…，an}。

以铅锭的化学成份为例：U={Pb、Ag、Cu、Bi、As、Sb、Sn、Zn、Fe、Cd、Ni、杂质总和}；V={Pb99.994、Pb99.990、Pb99.985、Pb99.970、Pb99.940}；而A的数值则需要根据协商的规则或者归一化法计算确定。

2.2.2建立隶属函数和评判矩阵

设rij是质量因数ui与各质量等级vj的隶属函数（本文选用了F函数中的梯形分布和半梯形分布函数），则：

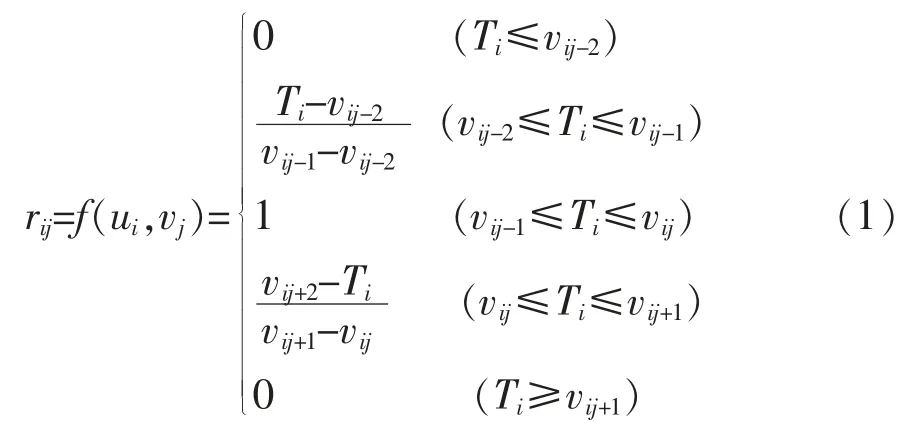
式（1）中：Ti是质量因子ui的实测值，vi是质量因子所对应质量等级的限值。

需要注意的是，因质量等级的限值可能是上限值、下限值和区间值等3种情况，应根据质量等级的限值情况，逐一对质量因数建立合适的隶属函数公式。

将各质量因子的实测值代入对应的隶属函数，即可得出各质量因子与各质量等级的隶属度，而从构成评判矩阵R，即：

2.2.3计算质量因子的权重集

质量因子的权重集A应根据评判标准或商定规则确定并进行归一化处理。若无规定，建议使用式（4）计算其权重值。

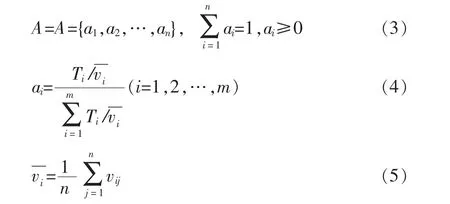
式（3）、（4）和（5）中：ai是质量因子ui的归一化权重值，Ti是质量因子ui的实测值，是质量因子ui的n级质量等级的算术平均值。

2.2.4质量评判的合成及评价

将质量因子的权重集和评判矩阵进行合成即可得到质量评判的结果向量B：

模糊评判的结果向量B为一维向量，包含n个元素，分别与n个质量等级相对应；大宗商品的质量评判结果由B中数值最大元素所在的位置确定（即：若bk的数值最大，则该商品应判定归属于第k级的质量等级）。

如果产品质量的影响因子涉及多方面，难以同时合理确定出所有因素的权重数，则需采取多级质量评判模型，先分别对每一大类的子质量因数进行权重集和评判矩阵的合成，再对所有大类的质量因子进行权重集和评判矩阵的合成及评价。式（7）是二级综合质量评判的合成公式，更多级别的综合评判模型可类推。

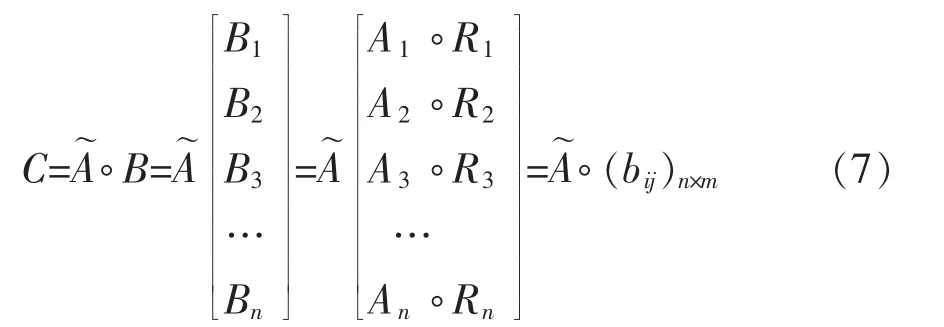
式（7）中：C是最终的综合评判结果，Bi是各大类质量因子的评判结果，是各大类质量因数的权重集，Ai是每一大类内的子质量因子的权重集，Ri是每一大类内子质量因子的评判矩阵。

3 模糊评判法的应用示例

3.1 方法概要

根据GB/T 469-2013的规定，铅锭的质量指标主要包括化学成分、表面质量、其他要求（包装、标志和质量证明书）等三大类。根据上述模糊评判法的评判模型，首先分别对化学成分、表面质量和其他要求进行分类质量评判（先根据式（1）、（3）、（6）建立隶属函数并计算权重数集、评判矩阵，再合成评判结果B化、B表、B其），再进行二级综合质量评判（根据式（7）合成综合质量评判结果C）。

3.2 应用示例

表1是按照GB/T 469-2013对6种（分别为甲、乙、丙、丁、戊、己）铅锭进行检测的结果数据（为便于计算，表面质量和其他要求均以检测结果合格率百分数表示）。

表1 6种铅锭的质量检测结果

3.2.1分类质量评判

以“化学成分”这一类质量指标为例，按照GB/T 469-2013中铅锭牌号及其化学成分含量范围，将化学成分的质量指标分为5个质量等级（即：Pb99.994、Pb99.990、Pb99.985、Pb99.970、Pb99.940）。根据前述的质量评判模型，参照5个质量等级中各个元素含量的限值，对各个元素的实测含量建立隶属函数（根据5个质量等级的元素含量限值特点，本文选用了F函数中的梯形分布和半梯形分布函数），以反映各个元素含量的实测值与5个质量等级限值的贴进度（接近程度）。表2是据此建立的Ag含量实测值与5个质量等级的隶属函数，其他元素可以此类推建立隶属函数。

表2 Ag含量实测值的隶属函数

续表2

表3中Ag元素的隶属度是将表1中“甲”种铅锭Ag元素含量的实测值代入表2中的隶属函数所计算得到的，同理，也可以计算出“甲”种铅锭的其他元素对于5个质量等级的隶属度。其他5种铅锭各个元素含量实测值对于5个质量等级的隶属度也可同理得出，在此不一一列举。

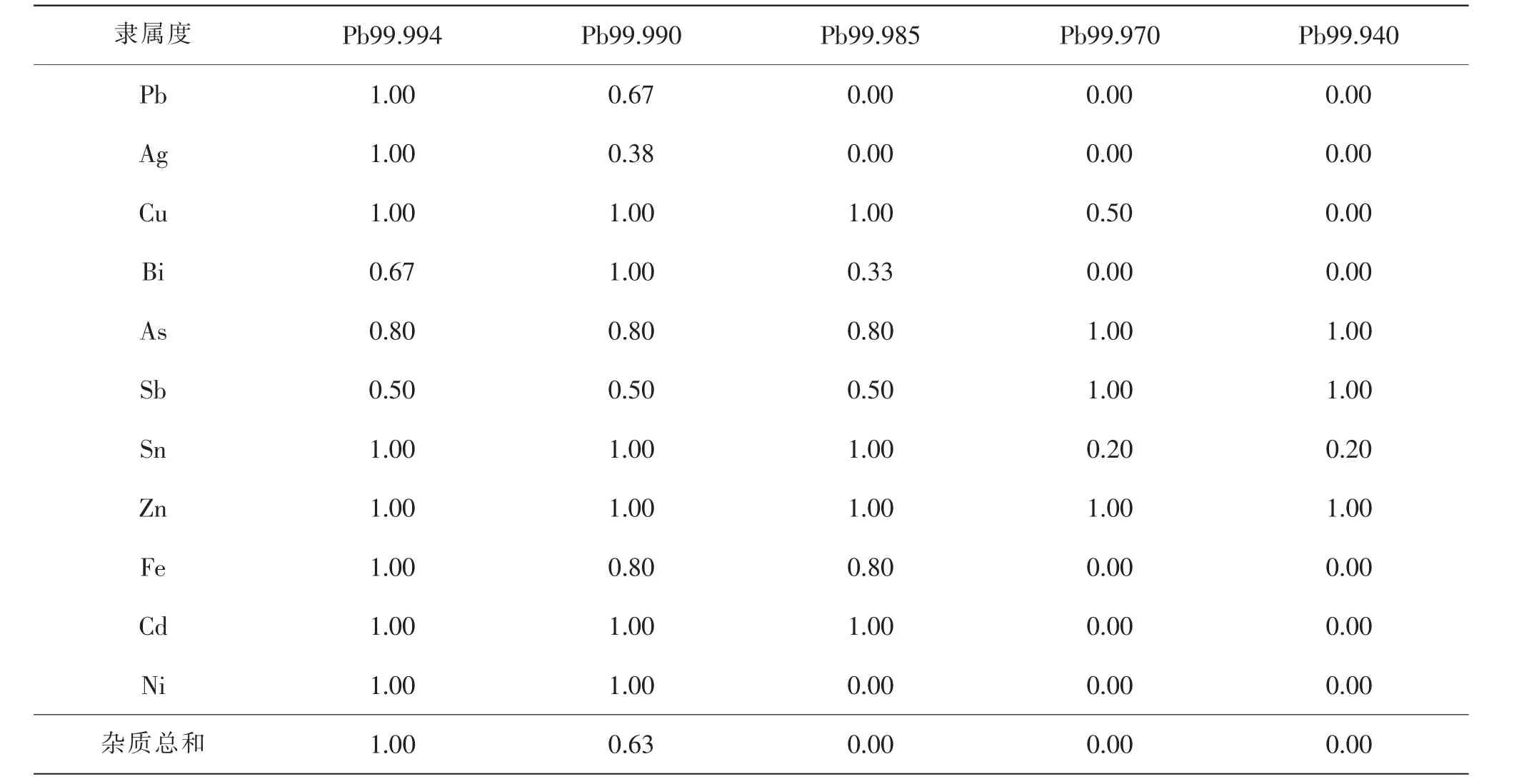
表3 “甲”种铅锭化学成分对于5个质量等级的隶属度

由表3可以得出“甲”种铅锭化学成分的分类质量评判矩阵R甲化，其他5种铅锭化学成分的分类质量评判矩阵也可以此类推得出。

根据GB/T 469-2013的表1中各质量等级对12种元素的限值，按照式（3）、（4）、（5）计算出“甲”种铅锭化学成分的权重集A甲化为：

则“甲”种铅锭化学成分的分类质量评判函数集（评判结果）为：

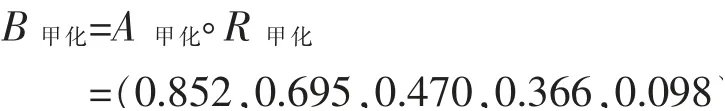
同理，可以计算出其他5种铅锭化学成分的分类质量评判函数集（评判结果）分别为：

而对于表面质量和其他要求（包装、标志、质量证明书）等指标，GB/T 469-2013中并未规定量化限值，供需双方在质量评判时可以商定各牌号等级的临界值，也可以不分级，仅确定一个合格与否的临界值。设定这些质量指标的合格率不低于80%即为合格，由此，可以得出其分类质量评判结果分别为：

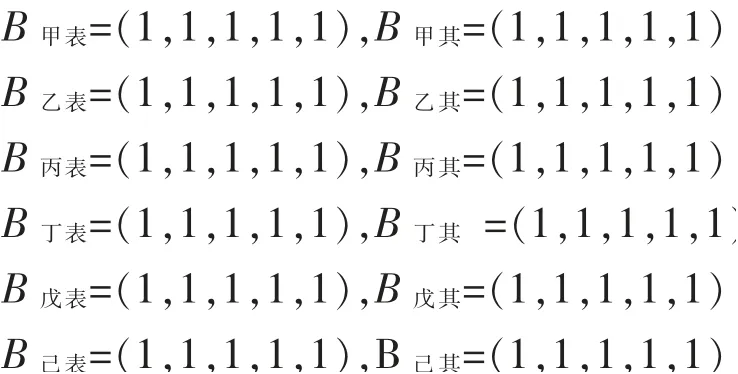
3.2.2综合质量评判

以“甲”种铅锭为例，其综合质量评判函数为：

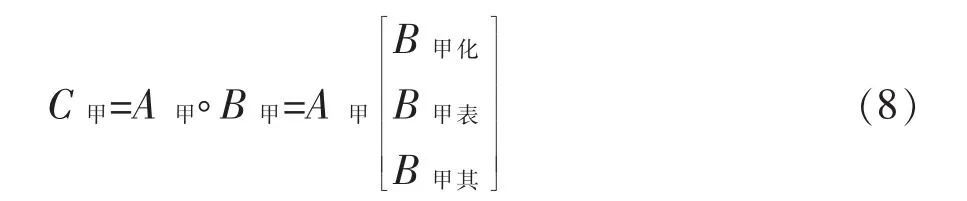
设定“甲”铅锭的化学成分、表面质量和其他要求（包装、标志、质量证明书）的权重分别为0.60、0.30、0.10，则A甲=（0.60，0.30，0.10），将A甲、B甲化、B甲表、B甲其的函数集代入式（8）中，即可得出“甲”种铅锭的综合质量评判集（评判结果）为：

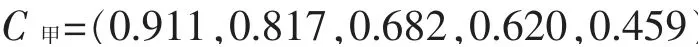
同理，可计算出其他5种铅锭的综合质量评判集（评判结果）为：

根据以上5种铅锭综合质量评判结果中最大数据所在的位置可知：“甲”、“乙”、“丙”等3种铅锭判定为Pb99.994牌号级别的产品，“丁”、“戊”2种铅锭判定为Pb99.985牌号级别的产品，“已”种铅锭则判定为Pb99.970牌号级别的产品。

3.3 模糊评判法与常规评判法的比较分析

从这6种铅锭质量指标的实测数据来看，若按照常规质量评判方法，则“甲”、“乙”、“丙”、“戊”4种铅锭属于Pb99.970牌号级别的产品，“丁”、“己”2种铅锭劣于Pb99.940牌号级别的产品。这一结果与3.2.2中利用模糊评判法得出的结果存在显著差异。

毋庸置疑，无论是从主元素（Pb）含量的实测数据来看，还是从杂质元素的实测数据来看，模糊评判法的评判结果更为科学合理，可以很好地反映出各元素含量与各质量等级限值的接近程度和符合程度，避免了常规评判法中因个别杂质元素含量超标而导致该铅锭的质量等级被降级评判。

由此可见，相比于常规质量评判法，本文所提出的模糊评判法不仅能量化表征各质量指标实测值与评价标准（限值）的符合程度，将定性问题通过定量方法来解决[5]，还能统筹兼顾各质量指标对其总体质量的影响，具有较好的客观性和合理性。可见，利用模糊评判法能准确客观地评判大宗商品的总体质量，使其恰如其分地用于生产制造。

4 结论

本文以铅锭的质量评判为例，对所提出基于模糊数学原理的大宗商品质量评判方法（模糊评判法）的理论基础、典型模型、应用示例和显著优势进行了阐述和分析，得出如下结论：

（1）基于模糊数学原理的模糊评判法具有量化“模糊性”和“贴近度”的突出特征，能综合考量各质量指标对总体质量的影响，避免由于人为主观因素的造成偏差；

（2）将模糊评判法应用于大宗商品的质量评判，不仅能客观、量化地反映产品质量指标实测值与其评判要求的符合程度，还有助于准确定位产品的总体质量水平，避免生产过程中对大宗商品实施不适当的“降级适用”造成的误用或浪费。