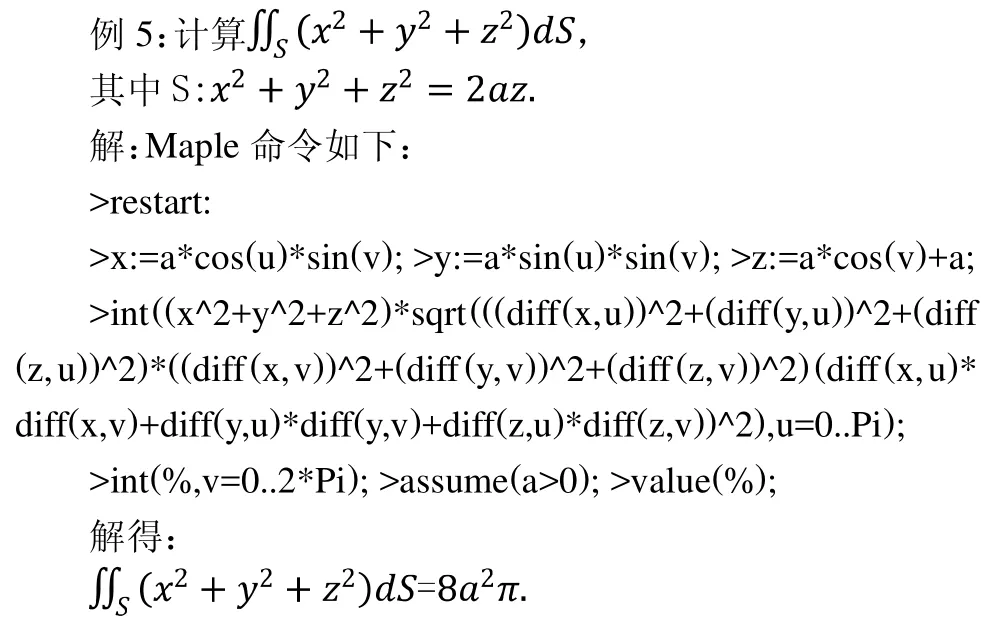Maple在积分中的应用

贺志英 何金阳 许 涵 刁良正 周宇扬 张志远

（中国矿业大学（北京）理学院 北京 100083）

0 引言

数学分析是数学类专业的重要主干课程，它在各个学科及相关领域中有着极广泛的应用，学习数学分析不仅是为了获取书本上的知识，更是为了锻炼提高数学的逻辑、抽象思维等。数学分析作为一门基础必修课程，很大程度上衔接了其他主干课程，例如为常微分方程、复变函数、实变函数、概率论与数理统计等后续课程供必要的基础知识和应用工具。数学分析是对微积分理论体系的严格化和精确化，它具有严密的推理、完备的体系、经典的方法、严谨的思维等许多特点，而且数学中的许多新思想、新方法、新应用等都起源于数学分析，其理论和方法已经是自然科学思想中不可或缺的重要部分。

因此，数学分析是数学类专业学生学习过程中的重中之重，而积分的内容又是数学分析中不可或缺的部分。定积分、二重积分、三重积分以及线面积分统称为黎曼积分，学习它们的关键是积分的定义与积分的计算，与之密切相关的是由函数、方程确定的空间图形。本文主要利用Maple软件求解定积分、重积分、线面积分。

随着符号计算软件Maple的不断发展与完善，越来越多的被引入到数学学科中作为解决实际问题的工具之一。Maple是加拿大Waterloo大学符号计算研究小组于80年代初研发出的一种强有力的符号计算软件。它具有范围广泛的符号计算、数值计算、函数作图功能，受到众多数学工作者的青睐。借助Maple软件强大的图形绘制技术完成平面积分和空间积分中一些复杂积分区域的绘制，会起到事半功倍的效果。

1 Maple在定积分中的应用

Maple可将积分的每一步骤进行详细的展示，并且说明每一步具体使用了什么方法。对于定积分的基本积分法：换元积分法、分部积分法，下面我们展示两个例子说明Maple是如何将详细步骤展示出来的。

结果如图2所示。

图2

结果见图3。

图3

2 Maple在重积分中的应用

2.1 积分思想的动态模拟

利用Maple软件编制程序来模拟二重积分的“分割、近似、求和、取极限”的数学思想。

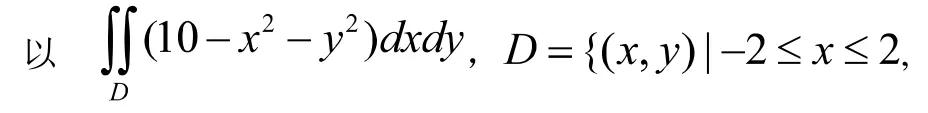
2.2 绘制复杂的积分区域并计算重积分

在求解二重积分或三重积分相关问题时，积分区域和被积函数的特点是解决问题的关键，利用Maple可以快速精确的画出积分区域，以便直观观察。

首先利用Maple画出图像（图4），

图4

根据曲面面积公式：

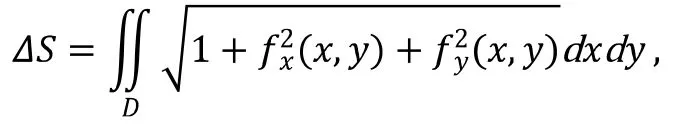
3 Maple在线面积分中的应用

曲线积分和曲面积分的积分对象都是函数。函数如果在曲线或者曲面上，则将曲线或者曲面方程代入到被积函数中，之后根据题意选择合适的投影方式将曲线积分和曲面积分变成普通积分。

3.1 计算曲线积分

曲线做投影时，要考虑曲线的方向和轴正向之间的夹角：夹角为锐角，方向角的余弦取正号；夹角为钝角，方向角的余弦取负号；夹角为直角，方向角的余弦为0。

3.2 计算曲面积分

曲面投影到平面上，则考虑曲面的法方向和平面的正法方向之间的夹角：夹角为锐角，方向角的余弦取正号；夹角为钝角，方向角的余弦取负号；夹角为直角，方向角的余弦则为0。