反磁项对Casimir-Polder力的影响
王 婷,龙玉梅,杨 慧,张 雪,郑泰玉,孙迎春
(1.东北师范大学物理学院,吉林 长春 130024;2.长春理工大学理学部,吉林 长春 130024)
运用量子电动力学研究物质与电磁场之间的相互作用时,得到一个重要结论,即真空中的电磁场具有零点能涨落,也称为真空能量.真空能量在特殊情形下产生的可观测效应为Casimir效应.1948年Casimir和Polder预言真空中两个中性原子之间或一个中性原子与一块理想导体板之间存在着一个相互吸引力,即Casimir-Polder力[1].1993年C.I.Sukenik等[2]在实验上测量了Casimir-Polder力;1997年,文献[3]第一次在加热环境下测得了超冷铷原子与石英下表面之间的Casimir-Polder力;D.M.Harber等[4]的研究缩短了原子与板之间的测试距离,同时实验表明Casimir-Polder力不仅有吸引力还有排斥力[5-7];参考文献[8-9]的研究显示反磁项会对Casimir力产生一定影响.本文在研究一个二能级原子与含电介质的一维输出耦合腔壁的相互作用中也考虑了反磁项,通过数值分析,讨论反磁项存在与否对原子与腔壁之间的相互作用力的影响.
1 理论模型
本文研究二能级原子与含电介质的一维输出耦合腔组成的体系[10],设二能级原子的跃迁频率为ω0,并处于区域Ⅰ中的x0处,如图1所示.x=-l为理想导体壁,x=-l到x=0的区域Ⅰ内充满均匀电介质,区域Ⅰ和区域Ⅱ之间存在耦合;区域Ⅱ为真空,x=L处为理想导体壁,且L≫l.

图1 系统模型
根据文献[11]的腔场量子化电磁场,体系的哈密顿量为
H=H0+HI.
(1)
其中H0为自由的哈密顿量,其表达式为
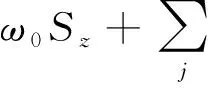
(2)
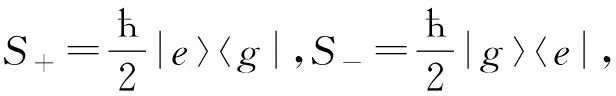
(3)
HI为相互作用哈密顿量[9],其表达式为
(4)
其中第2项为反磁项,gj为耦合系数,公式为
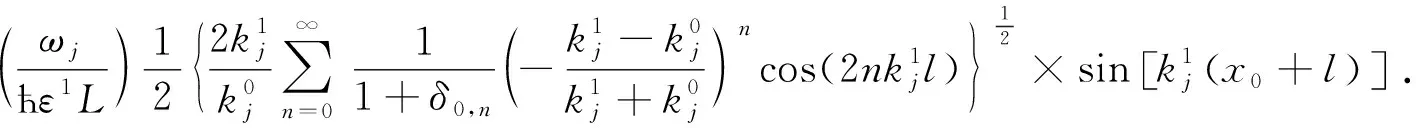
(5)
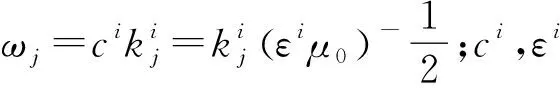
2 原子与腔壁之间的Casimir-Polder力
Casimir-Polder力由势能对原子位置求负梯度得到,即
(6)
其中ΔE(2)为系统二阶能移,其表达式为
(7)
设系统处于缀饰基态,根据微扰理论计算可得

(8)
将(8)式代入(7)式得

(9)
(10)
(11)
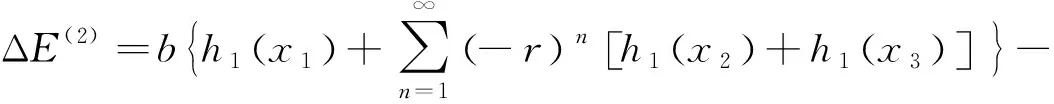
(12)
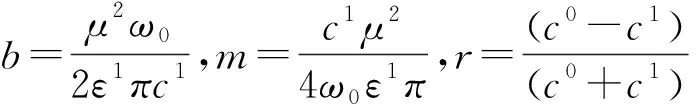

(13)
其中h3(x)为
(14)
3 数值分析
以上得到了Casimir-Polder力的解析表达式.通过数值分析讨论反磁项对Casimir-Polder力性质和大小的影响.
图2表示原子处在x0=-2.5×10-8m(原子x0=0的边界附近)时,Casimir-Polder力随腔长变化的示意图.其中,腔长变化范围为0~-2×10-7m,原子的跃迁频率为ω0=1×1014Hz,反射率为r=0.33,实线表示HI中不包含反磁项,虚线表示HI中包含反磁项.由图2可以看出:无论是实线还是虚线Casimir-Polder力的值均为负值,即原子与腔壁的相互作用是吸引力,这说明考虑反磁项并不能改变力的性质.另外,从图2也可以看出 Casimir-Polder力随腔长的增大而减小.但是两条曲线显示的力大小不同,虚线的力大于实线的力.这说明考虑反磁项会增加力的大小,有利于Casimir-Polder力的测量.

x0=-2.5×10-8 m,=0~-2×10-7 m,ω0=1×1014 Hz,r=0.33
4 结论
本文研究了二能级原子与含电介质的一维输出耦合腔壁之间的相互作用力,在构造含有反磁项的系统哈密顿量的基础上,利用微扰理论和zata函数重整化理论获得了系统缀饰态下的二阶有限能移,并给出了Casimir-Polder力解析表达式.通过数值分析讨论反磁项对力的影响.结果表明:增加反磁项虽然没有使Casimir-Polder力的性质发生变化,但反磁项增大了力的大小.本文的研究结果为进一步研究Casimir-Polder力提供了理论参考,在今后的研究中,将在其他光学腔中研究反磁项对其的影响.

