自编限量活页作业的优化设计

徐跃良

[摘  要：自编限量活页作业是一种响应我校教学理念，切实为学生减负的教学模式。它力争巩固学生的基础知识，活跃学生的思维，挑战学生的能力，可谓“面面俱到”。但如何才能做到真正的“面面俱到”，从精选题目，难易适度，分层练习，变题变式等方面谈谈如何对自编限量活页作业进行设计和选择。试图从自编限量活页作业的优化设计入手，提高学生学习的有效性，减轻学生的课业负担，从而激发学生学习的兴趣。

关键词：初中数学;活页作业;优化设计]

自编限量活页作业是一种有目的、有指导、有组织的学习活动，是学生掌握知识、形式技能、发展智力的基本途径。作为日常教学的一个组成部分，活页作业的设计和选择是至关重要的。

要想有效地改变学生课后作业负担过重的状况，必须有效地提高课后作业的效率——“自编限量活页作业”改革势在必行。

一、自编限量活页作业的优化设计

新课程与教学观引领的活页作业的设计，不只是关注学生对知识要点的掌握与否，更应关注学生能否运用数学知识解决实际问题，关注学生的实践能力和创新能力的培养，关注学生在数学问题领域的情感、态度、价值观生成的意向和程度等方面。为此，根据几年来的数学教学实践，以及活页作业编制的实践经验，本人通过对活页作业的设计的思考，浅谈如何从以下几个方面对活页作业进行优化设计。

1.精编细选，适合学生

初中数学教学的目的不是培养只会背数学概念、公式、定理，只会解答数学题的应试性学生，而是要培养具有一定数学素养的创造性人才，是以促进学生的素质发展为根本目的。因此自编活页作业的设计要有针对性，选题时一定要依据课程标准，根据每节课的教学目标、教学重难点来精心设计安排。按学习过程，我们可以将练习分为必做练习和选做练习。

（1）必做作业

作业的意图重在巩固学生的基础知识。所以必做练习应根据新知的基础应用及学生的认知特点进行设计，充分利用新知识的特点， 进行巩固与诱思，目的在于知识的巩固和正迁移。

例如，《2.2等腰三角形的性质》这一课时，可以设计这样一组必做习题：

1.已知等腰△ABC中，AB=AC，且[∠B=θ]，则[θ]的取值范围是（         ）

（A）[θ≤45°]    （B）[0°<θ<90°]    （C）[θ=90°]     （D）[90°<θ<180°]

2.若等腰三角形的一个外角为140°，则它的顶角为（        ）

（A） 40°        （B） 100°        （C） 40° 或100°       （D） 不确定

3.等腰三角形一腰上的高与底边的夹角等于（        ）

（A） 顶角     （B） 底角      （C） 顶角的一半   （D） 底角的一半

4.在等腰三角形中，设底角为x°，顶角为y°，则用含x的代数式表示y ，得y =____________________，则用含y的代数式表示x，得x =__________________，

5.如图（第7题）所示，已知∠O=35°，CD为OA的垂直平分线，则∠ACB的度数为__________________.

6.如图（第8题）所示，若BE平分∠ABC，DE=BD，则DE和BC的位置关系如何？并说明理由.

这些练习的目的，一方面是对等腰三角形的相关性质进行巩固，如等腰三角形的三线合一、等角对等边、等边对等角;另一方面是为后面的应用作铺垫、扫清障碍。通过这些必做练习，学生可以准确的了解等腰三角形的性质的内容，并正确地使用它。

（2）选做作业

选做练习应根据知识的重点、难点、关键点，进行设计，其目的在于有效地巩固所学的新知识。在编制此类练习时要突出对知识点的理解、把握和活用。通过这些练习，有助于学生数学能力的形成和对数学本质的领悟，培养学生举一反三，触类旁通的能力。

例如，《2.2等腰三角形的性质》这一课时，可以设计这样的选做习题：

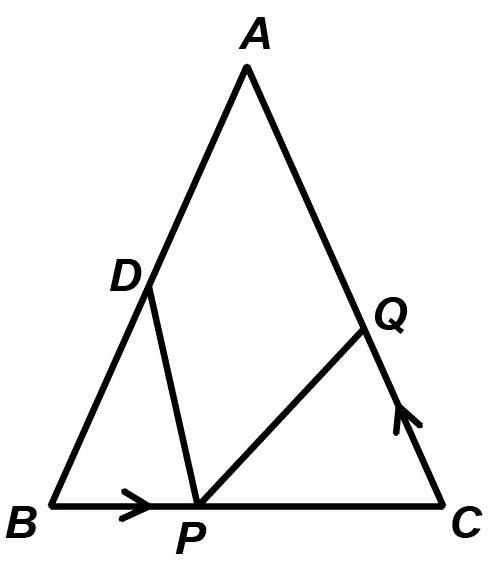
如图所示，在△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点.

（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动.

①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等？请说明理由;

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC的三邊运动，则经过多长时间，点P与点Q第一次在△ABC的哪条边上相遇？

本题涵盖了等腰三角形的基础知识，同时还渗透了动点问题，从而引发的分类讨论，为日后的分类思想作了很好地铺垫。具有承上启下的作用。

2.难易适宜，促进发展

学生接受和巩固知识是一个由简单到复杂、由易到难、由浅入深的过程，因此活页作业的设计既要照顾基础，不机械重复，也不能忽难忽易，必须符合学生的思维及认识规律，遵循“小台阶，步步高”的原则。

3.分层作业，实现自主

活页作业是为“自我检查”服务的，必做作业和选做作业之分让学生彻底实现自主选题;其中，必做作业它所涉及的知识面要宽，综合性不能太强，以简单题、小题、运算量不大的题为宜;选做作业要活，以综合性强题为要。当然难易的定位要根据学生情况而定。复习课难度自然可有所提升。

例如，八年级上册第二章的复习课作业可有如下设计：

必做作业

1.已知等腰三角形的周长为40cm，以一腰为边作等边三角形，其周长为45cm，则等腰三角形的底边长是（    ）

A.5cm            B.10cm          C.  15cm         D.20cm

2.等腰三角形的顶角为120°，腰长为2 cm，则它的底边长为（      ）

A. [3]cm        B. 3[3]cm      C. 2cm         D. 2[3]cm

3.正三角ABC所在平面内有一点P，使得△PAB，△PBC，△PCA都是等腰三角形，则这样的P点有 （  ）

A.1个          B. 4个           C.7个         D.10个

4.如图，∠A=15°，AB=BC=CD=DE=EF，则∠GEF=_______________________.

5.如图，在△ABC中，∠A= 80°，点D，E，F分别在BC，AB，AC上，且BD=BE，CD=CF.则∠EDF的度数为___________________.

6.在△ABC中，已知AB=AC.

（1）如图①，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=___________________;

（2）如图②，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=___________________;

（3）思考：通过以上两题，当AD是BC上的高，AD= AE时，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：___________________.并说明理由.

选做作业

如图，已知△ABC中，AD⊥ BC，， ∠B=2∠C，试说明AB+BD=CD的理由.

4.变题变式，加强思维训练

所谓变式就是变换直观材料或事物呈现的形式，使教学对象的非本质属性得到变异，而本质属性保持不变。巧妙运用变式，能有效地避免题海战术，达到巩固数学知识的效果;同时可以培养学生独立思考，举一反三的学习态度。通过变式作业，可以给学生提供自主探索的机会，充分的思考空间，让学生在观察、实验、归纳、分析的过程中去理解数学知识的形成和发展过程，进行数学的再发现、再创造，培养学生的思维能力。教师在设计作业的时候，要注意适当扩大作业的思维含量;要最大程度地引导他们进行变题变式训练，使一个问题与有关问题联系起来，从而使问题层层深入，思维不断深化，使学生真正辨清概念、理解题意。

变式训练应抓住思维训练这条主线，恰当地变更问题情境或改变思维角度， 培养学生的应变能力，引导学生从不同的途径寻求解决问题的方法。培养学生的发散性思维和灵活的思维品质。

例如，在《直角三角形》一课时内容中，编制变式题如下：

将一副直角三角板如图所示放置，等腰直角三角板ACB的直角顶点A在直角三角板EDF的直角边DE上，点C、D、B、F在同一直线上，D、B是CF的三等分点，CF=6，∠F=30°.

（1）三角板ACB固定不动，将三角板EDF绕点D逆时针旋转至EF∥CB（如图2），试求DF旋转的度数;点A在EF上吗？为什么？

（2）在图 （2）的位置，将三角板EDF绕点D继续逆时针旋转15°.请问此时AC与DF有何位置关系？为什么？

上述题目是通过变条件达到变式的效果，还可以通过变图形、变结论、变条件与结论达到变式的，在此不作一一列举。总之一句话，变式可以发散和灵活学生的思维。是编制活页作业时的一大选择。

二、实践后的体会和反思

两年年来笔者响应学校号召，在同组人的分工协作下，通过有效地编制活页作业，有效地提高了作业的有效性，减轻了学生的学业负担。让每个层次的学生通过分层作业，体会到了成功的喜悦，从而对学习数学产生了极大的兴趣。经过两年的努力，我们学校的学生的整体水平有了很大的提高，特别是班里学困生（成绩不合格）的比例也有了大幅度的下降。

同时，个人作了如下几点反思：①由于活页作业的编制是一项工作量比较大的工作，需要教师投入大量的時间和精力，因此我们学校采用的是集备课组力量，集体备课、编制活页作业。并分课时按个人负责制完成，由于是提前编制作业，可能前后两名老师之间会出现重复编制现象，故提倡分章完成;②在活页作业编制好之后，作业的批改也是至关重要的，教师务必及时批改学生的作业，及时发放作业，以便作及时的反馈。③活页作业的订正尤为重要，做作业的目的本身是查漏补缺，如何有效地落实学生对活页作业的及时订正还有待进一步的探究和实践。

浙江省平湖市独山港中学  314203