人体呼吸CO2浓度监测模型及其实验验证
郭竹睿,熊 涛,郑 刚,Song Shigeng,周 顺
(1.西安工业大学光电工程学院,陕西 西安710021;2.西苏格兰大学薄膜、传感器与成像研究所,英国 佩斯利PA1 2BE)
呼吸信号的监测在临床上对人体生命健康有着重大意义,人体吸入到肺部的O2运输到全身参与新陈代谢,产生的CO2通过呼吸作用排出体外,因此对于CO2浓度的分析可以反应人体部分疾病信息[1-2]。呼气末CO2分压(PETCO2)与体温、血压、脉搏等同属于基本生命特征,其在麻醉、急诊、重症监护等医学领域有广泛的应用[3]。
呼气末CO2(ETCO2)监测是临床针对危重病人的重要监测参数之一,Cinar等人[4-5]通过对病人进行ETCO2监测实现生命体征判定。目前常使用的CO2监测设备主要是基于非分散红外(NDIR)原理设计的CO2传感器,按照传感器监测模块的位置又可以分为主流式与旁流式[6-8]。关于人体ETCO2监测的研究,大多都集中于传感器的结构与临床分析,在呼吸传感模型方面报道较少[9-11]。现有的发展比较成熟的呼吸模型主要分为以下两类:一类是基于中枢神经的反馈控制建立[12-13],这类模型通过分析动脉血中O2与CO2分压的变化,重点研究大脑的神经调节与中枢控制等机制,模型求解复杂,不能详细的体现呼吸过程中气体浓度的变化情况[14-15]。另一类是通过临床病例收集,以大数据为基础、基于Logistic回归分析建立的呼吸疾病风险预测模型[16],这类模型利用统计学原理来判定疾病预测因子,进行风险评分来建立早期预警模型,模型使用受限,并且不能体现肺部呼吸的情况,更无法进行呼吸监测[17-18]。
一般的呼吸模型都是基于自身研究需要所建立的,对于完整体现呼吸时肺部情况的模型仍然比较少,并且尚不完善。本文从物理学角度对呼吸运动进行分析,重点研究在呼吸过程中肺内气体浓度的变化。除了建立呼吸模型,本文还考虑了传感器监测结果与肺内实际情况的差异性,建立了CO2传感器模型,模型的求解结果与NDIR传感器实验数据基本一致。因此,此模型可以真实反映传感器测量与肺内实际情况的差异性,并且可应用于呼吸监测。
1 呼吸模型的建立
呼吸运动指的是人体与外界环境之间进行气体交换的过程。每个呼吸周期可分为吸气阶段和呼气阶段,本模型依据此建立了由吸气与呼气阶段组成的分段模型。
从生理学角度分析,人的呼吸包含三个环节,分别为外呼吸、气体在血液中的运输、内呼吸,整个呼吸过程如图1所示。

图1 人体呼吸过程示意图
本模型主要研究在呼吸过程中,肺内O2与CO2气体浓度变化的动态过程,如图1所示,主要影响因素为外呼吸。外呼吸包含肺通气与肺换气两部分,肺通气指的是肺部与外界环境之间的气体交换,即呼气与吸气过程,该过程是由肺内与外界环境之间的压强差引起的;肺换气指的是肺部与血液之间的气体交换,交换方式为物理扩散,交换动力为气体间的浓度差。
人体在吸气过程中,气体从外界环境进入肺内(肺通气),改变了肺内气体浓度与肺部体积。同时肺泡与血液间的气体交换(肺换气)将O2扩散至血液中,并将人体代谢产生的CO2扩散到肺内,最后通过呼气过程(肺通气),将气体排出体外。
依据此呼吸过程建立呼吸模型:首先需要建立呼吸速率与吸入、呼出气体量之间的关系;其次需考虑肺换气时O2与CO2气体扩散率不同造成的气体体积差并建立肺内气体浓度变化方程;由于本模型的气体浓度通过体积比表示,所以应同时建立肺部总体积的变化方程。
1.1 呼吸速率方程
由一级反应动力学可知,反应速率仅与反应物的浓度成比例关系[19],如式(1)所示,其中t为反应时间,C(t)为t时刻反应物浓度,k为一阶动力学反应速率常数,负号表示反应物含量在降低,则反应速率可以表示为:

同理可以认为,呼吸速率仅与肺通气时吸入或呼出的气体量浓度成比例关系;由此建立吸气速率与呼气速率的微分方程:

式中:Vmin为平静呼吸时肺部的最小体积。Vmax为平静呼吸时,肺部的最大体积,即为Vmin与吸入气体量之和。用I、E区分吸气与呼气阶段,VI(t)代表吸气过程中t时刻吸入的气体量,VE(t)代表呼气过程中t时刻呼出的气体量;VL(t)代表t时刻肺部的体积;k为反应速率常数;̇V为常数项,物理意义为基础呼吸速率。
1.2 气体浓度变化方程
肺内气体浓度通过体积比进行计算,假设在时间t时,肺内目标气体(O2或CO2)浓度为c(t),经过一段时间Δt后,目标气体浓度为:

式中:c(t)VL(t)为t时刻肺内目标气体的体积。α表示肺扩散速率,单位为mL/(s·mmHg),ΔP为目标气体分压差,αΔPΔt体现了Δt时间段内肺换气过程。时间段内,肺通气过程中吸入或呼出气体中包含的目标气体体积,其中c1(t)为吸入气或呼出气中目标气体浓度。VL(t)为t时刻肺部体积,为在Δt时间段内肺部体积的变化量。
由微分方程定义可得到浓度随时间变化的微分方程,当Δt取值无限小时,公式可简化为
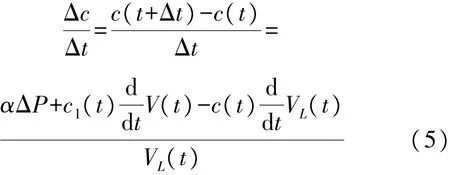
式(5)即为肺内O2或CO2气体浓度随时间变化的微分方程。
在吸气阶段,吸入气体中目标气体浓度c1(t)即为空气中O2与CO2的浓度,O2为21%,CO2为0.04%,肺内压强与大气压强相同,为760 mmHg(1个标准大气压)[20];可得如下方程:

式(6)、式(7)分别为吸气过程中肺内O2、CO2浓度变化方程。其中αO2.I与αCO2.I分别为吸气过程中O2与CO2的肺扩散速率,PO2.B与PCO2.B分别为血液中O2与CO2的分压。
在呼气阶段,呼出气体中目标气体浓度c1(t)即为c(t)。因此,由式(5)可得目标气体浓度变化率为:

依据式(8),分别构建肺内O2与CO2浓度变化方程:


式中:αO2.E与αCO2.E分别是呼气过程中O2与CO2的肺扩散速率。
1.3 肺部体积变化方程
吸气时肺的总体积变化为肺的最小体积Vmin加上吸入的气体量,以及O2与CO2浓度变化产生的体积差。所以吸气时肺部体积变化方程为:
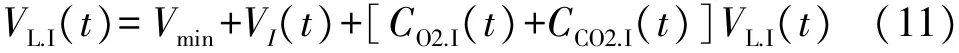
对式(11)两边同时求导,得到吸气过程中肺体积变化率的微分方程:
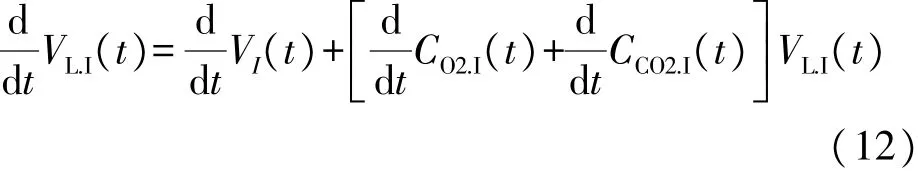
同理,呼气时肺的体积变化率为:
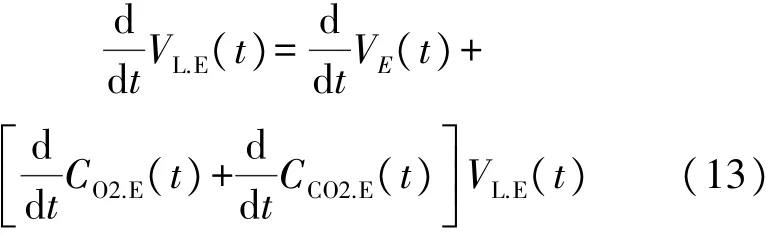
至此,得到了完整的呼吸模型,模型为分段函数形式,一个周期即为一个完整的呼吸时长;其中吸气阶段由式(2)、式(6)、式(7)、式(12)四个微分方程联立求解即可得到,呼气阶段由式(3)、式(9)、式(10)、式(13)四个微分方程联立求解可得。
2 呼吸模型仿真结果
各参数的赋值及物理意义如表1所示。

表1 模型中的参数数值[21-22]
联立式(2)、式(6)、式(7)、式(12)四个微分方程组并标定初始值即可求解吸气过程中气体浓度变化,其中肺内O2的初始分压为104 mmHg,CO2为40 mmHg[21]。联立式(3)、式(9)、式(10)、式(13)四个微分方程组,将吸气末的数据值标定为初始值即可进行求解,得到呼气过程中气体浓度变化。本模型求解的气体浓度均由体积比表示,与肺内压强相乘即可得到气体分压。
正常成人呼吸频率为12次/min~20次/min,吸气呼气的时长比约为1∶1.5~2,这里取平均值,取值1 min呼吸频率16次,吸气与呼气的时长比1∶1.75,计算可得一个呼吸周期T=3.74 s,吸气时长tI=1.36 s,呼气时长tE=2.38 s。以吸气末、呼气初为起始点绘图[21]。
如图2所示为本模型所构建的人在平静呼吸时,肺内O2浓度变化波形图,横坐标表示呼吸时间,纵坐标表示O2体积与肺部体积之比。可以清楚的看到在吸气与呼气阶段,肺内O2浓度的变化速率完全不同。在呼气阶段,O2浓度减小的非常快,近似线性。
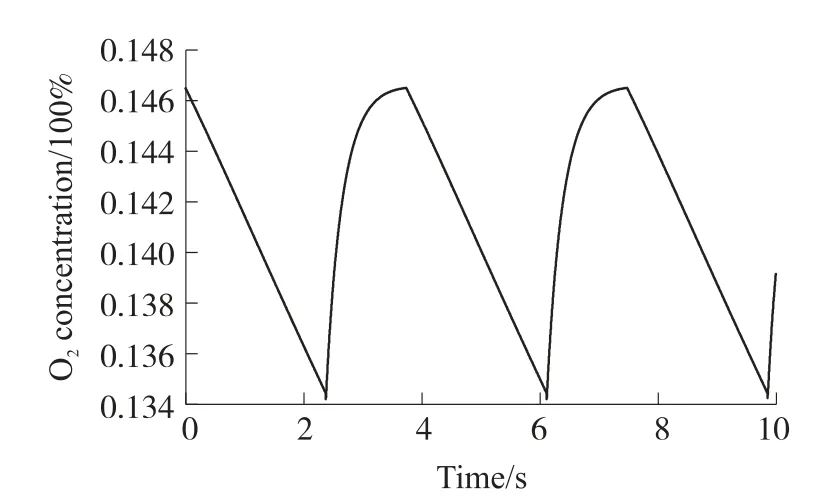
图2 肺内O2浓度变化波形图
同样的分段函数构造方法,构建肺内CO2浓度变化波形图:
如图3所示,清晰的反映了呼吸过程中肺内CO2浓度的变化。在呼气阶段,CO2浓度逐渐增加,增加的速率逐渐减慢直至呼气末;达到呼气末峰值后,在吸气时CO2浓度迅速降低,后趋于平缓。

图3 肺内CO2浓度变化波形图
3 传感器模型
呼气末CO2监测在临床中已经有了广泛的应用,但真实的肺内气体浓度与传感器所测得的呼出气浓度并不完全相同,故基于第2节提出的呼吸模型,扩展建立CO2传感器模型。
3.1 CO2传感器模型
完整的呼吸模型分为吸气阶段与呼气阶段,传感器模型也是同样。首先构建理想的传感器模型,假设传感器探测气室体积无限小、响应时间无限快且数据采样间隔无限短。因此,在探测过程中传感器模型探测到的气体浓度会从上一个呼气末的CO2浓度迅速下降到空气中CO2的浓度,当吸气阶段结束时又会从空气中CO2浓度迅速上升为肺内呼气阶段的CO2浓度,则理想传感器模型如图4(a)所示。
由此可知,传感器所监测的气体浓度变化只有呼气阶段是真实有效的,和肺内实际情况是基本一致的,吸气阶段所监测到的浓度实际为外界环境中CO2浓度。
令传感器采样时间为tr,对采集的数据进行平滑处理,得到图4(b)。通过代入不同的tr值,可以发现tr值越小,即采样间隔越短,得到的波形图与理想传感器模型就越接近,从外界环境气体浓度过渡到呼气浓度的变化速率就越快;当tr值越大,传感器的采样率越慢,曲线就越光滑。

图4 CO2传感器模型波形图
3.2 CO2传感器简化模型
通过前面的分析可知,在实际传感器监测过程中,最有价值的是呼气阶段。虽然在第3节已对呼吸模型进行求解,得到CO2波形图,但求解复杂,整个微分方程组之间都存在相互反馈与影响,在实际应用中,不方便程序移植。故针对CO2传感器模型的参数进行简化,并进行数学计算,得到具有实际应用价值的单一变量函数解析式。特别是针对CO2传感器监测仪与呼吸机等,在进行数据采集与分析过程中,单一变量的简化模型更方便进行上位机程序的编程,也对下位机的数据采集具有指导意义。
呼气时肺体积变化范围为3 000 mL~2 500 mL,变化范围较小,因此将肺体积VL.E(t)简化为常数V=2 750 mL,对式(10)两边积分,积分的上下限分别为t=0到t=ts时刻,经过简化与计算得到式(14):

式中:只有ts一个变量,其余均为常数。对常数赋值后进行计算,并与呼吸模型求解结果进行对比,如图5所示。
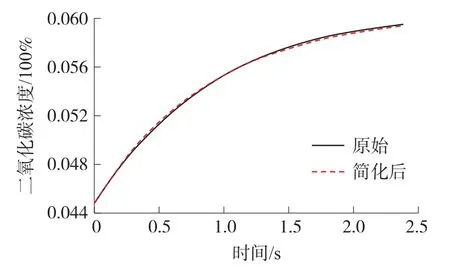
图5 CO2传感器简化模型与呼吸模型求解结果对比
图中,短点线代表的是CO2传感器简化模型,实线为原始呼吸模型,对比可以看出,经简化积分运算后得到的传感器简化模型依旧拥有较高的使用价值,与原呼吸模型求解结果的误差非常小。
4 实验验证
目前,人体呼吸CO2监测设备普遍利用CO2在中红外波段的吸收特性进行设计[23]。基于NDIR的CO2呼吸探测系统示意图如图6所示,主要包括四个部分:呼吸气室、红外LED、PbSe红外探测器及信号采集处理系统。

图6 主流式NDIR呼吸CO2监测系统示意图
如图6所示,通过电路部分实现光源的驱动以及信号的采集处理。本实验选用GSS公司红外LED,峰值波长为(4.3±0.15)μm,3 dB带宽为1μm,峰值波长随温度漂移量为6.3 nm/℃。为了保证光源的聚光特性,采用复合抛物面聚光器(CPC)实现光线汇聚输出。红外探测器部分PbSe为非制冷四通道探测器,本文只使用其中一个信号采集通道与其对应的参考通道,探测器感光区域面积为1 mm2,峰值灵敏度波长为3.8μm,峰值响应度为3×104V/W。
基于光源与探测器设计相应的气室结构与夹具,本实验采用主流式CO2监测系统,这种监测结构简单、更加类似人体呼吸管道,实时性较高。为了避免呼吸过程中水蒸气凝聚管壁,尤其是在光线通过的部分,采用可替换的呼吸主管道,实现多次重复使用。呼吸探测气室结构与夹具如图7所示。

图7 主流式NDIR呼吸CO2监测系统气室结构
在进行验证试验前,须先对传感器浓度进行标定。在标定实验中,把整个传感装置视为整体,将从传感装置输出的处理后的数据(电压幅值vs.时间)和对应的标准混合气的浓度值进行三阶最小二乘拟合获取拟合函数。测量时,利用拟合函数和当前浓度值进行数据映射便可得到CO2气体浓度信息,具体实验装置如图8所示。

图8 人体呼吸CO2浓度标定及监测实验装置图
实验时将监测系统的双通道输出响应分别接入示波器,使待测者调整好呼吸,避免有意识地控制呼吸节奏,待测者通过呼吸软管进行正常呼吸,示波器实时显示当前呼吸CO2波形图。
在室温、标准大气压环境下,对约15位健康志愿者进行呼吸CO2浓度的实时监测实验,监测系统输出接入示波器直接观察。实验结果具有高度规律性,整体变化形态几乎一致,随机采集两位测试者数据进行比对。监测到的两位测试者呼吸CO2波形图如图9所示。
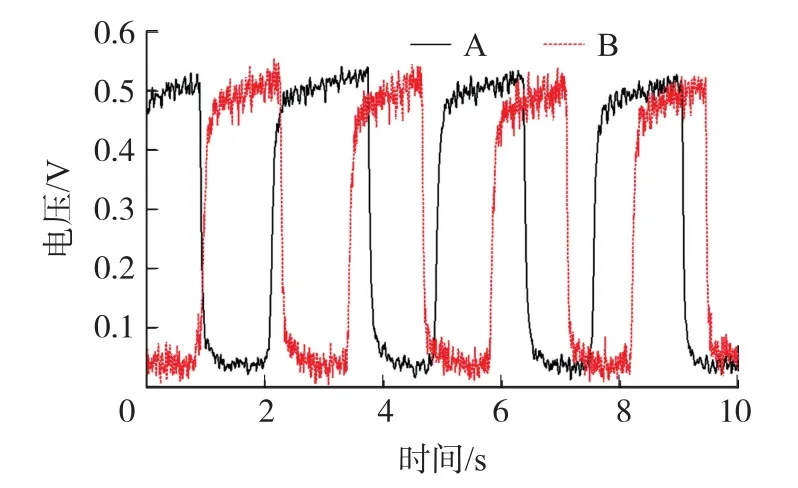
图9 两位健康测试者呼吸CO2浓度波形图
图9 中,A、B分别代表两位测试者,横坐标表示时间,纵坐标为示波器输出的包含CO2浓度信息的电压值。数据产生的毛刺现象是由监测电路系统引入的高频噪声与光源调制引入的抖动噪声引起,因此需要对数据进行滤波处理,并对输出电压与浓度关系进行映射,得到测试者A的监测波形图并与模型进行对比,如图10所示。

图10 CO2监测波形图与呼吸模型结果对比
图10 清晰地显示了呼吸CO2波形图变化规律,实测数据波形特征明显与呼吸模型匹配度较高,验证了呼吸模型的适用性。但其在波谷位置匹配度较差,分析主要原因为呼吸频率较快,探测气室内残留呼出气体,导致实测浓度值较高,但不影响对呼吸CO2浓度监测。
运用同样的方法对其他测试数据做相同滤波处理,并将实验中测得的参数值代入模型进行微分方程组的求解计算。将得到的模型与实验数据进行对比,得到结果如表2所示。

表2 15位测试者实验数据与模型数据对比
表2 列出了不同测试者的主要测量参数,实验值表示每位测试者3个完整呼吸周期ETCO2值的平均值,模型值表示通过模型计算得到的理论值[23]。将实验值与模型值进行对比,并计算误差。分析可得,在测量过程中,电路引入的噪声使得采集到的CO2浓度波形存在毛刺现象,造成判断呼气与吸气时长时存在差异,该差异是造成实验值与模型计算值的主要误差来源。通过对比实验数据与模型数据,误差小于0.3%,验证该模型具备实际应用价值。
6 结论
本文从分析呼吸的物理过程出发,依据肺部气体体积与浓度关系,建立了人体肺部呼吸模型、CO2传感器模型以及传感器简化模型,实现了CO2浓度监测。基于NDIR呼吸CO2传感原理,搭建实验监测系统,测试结果与建立模型匹配度较高,模型测量误差小于0.3%,可以实现人体CO2波形图的特征判定。本模型的建立是作为研究肺部呼吸的基础,可以进一步实现研究肺部在呼吸时的各种生理特征,对于呼吸CO2浓度监测仪器以及呼吸疾病分析具有很好的参考价值。

