支持快速撤销的ABE算法在个人健康记录云中的研究∗

李维勇，张 伟

(1.南京信息职业技术学院网络与通信学院，江苏 南京 210023；2.南京邮电大学计算机学院，江苏 南京 210003)

1 引言

个人健康记录(Personal Health Record，以下简称PHR)云[1]是云计算应用的一种延伸，它提供一种便捷的网络访问，方便病人以及医生随时随地上传、访问、分析以及使用各类健康信息。随着物联网、云计算等技术的全面发展，关于个人健康信息的数据呈现井喷式的增长，个人健康记录分享系统逐渐发挥出了在健康管理方面的优势，例如身体状态预测、疾病预防、病史分析、用药分析等功能。虽然方便了人们随时随地进行信息的交换，但同时也对病人的隐私造成了巨大的威胁[2]。目前在互联网上，国家、企业或者个人的隐私数据出现意外暴露的事件数不胜数，有的甚至被拿去作为商用从而获取非法利益。因此，当前PHR 系统急需一套严格的数据保护与访问权限控制技术，最理想的状况就是既可以实现数据的安全加密，又能够方便加密者们自己自由地制定各种各样的访问策略。然而传统的密码学算法并不具备这种数据分享的机制。即使是公钥加密算法，一个公钥加密的数据也只能发送给一个解密者。而从访问控制技术角度来看，传统的访问控制算法也仅支持可信的服务器制定和实施访问控制策略。

基于属性的加密体制[3－4](attribute-based encryption，ABE)是近些年来提出的一种功能加密体制，它拓展了传统公钥加密的范畴，在加解密操作中赋予一套访问策略以及具备一定描述性的属性集合，只要属性集合与访问策略之间足够相似，那么就能够在众多加密者与解密者之间实现安全的数据共享。相比一般公钥加密算法，ABE 不仅为加密信息提供了灵活的访问控制功能，还具备一定的容错性质，因此在指纹验证、虹膜验证、人脸识别等生物特征识别领域[5]具有潜在的应用价值，尤其在个人健康记录云当中[6]有着广阔的应用前景，填补了传统密码学在这方面的应用空白。具体来说目前主要有两种主流ABE 算法:一种是基于密钥策略的ABE算法[7](key policy attribute-based encryption，KPABE)，它将访问策略嵌入到密钥当中，而将属性集合则嵌入到密文当中；一种是基于密文策略的ABE算法[8](ciphertext policy attribute-based encryption，CP-ABE)，它将访问策略嵌入到密文当中，而将属性集合则嵌入到密钥当中。CP-ABE 在数据加密过程中支持数据属主自由制定访问策略，而密钥当中嵌入的属性集合又能够表征不同解密者的身份，因此CP-ABE 非常适合面向PHR 系统构建安全又灵活访问控制机制。

尽管CP-ABE 具备了传统数据加密和访问控制算法所不具备的独特性质，但是其距离实际应用仍然相距甚远。其中最关键的问题就是如何实现高效的、安全的、细粒度的属性撤销机制。在绝大多数应用场景下，属性都是动态变化的，其中包括系统级属性变化(系统新增或者删除某个属性)、用户撤销(注册新用户或者注销旧用户)、以及属性级撤销(用户增加属性或者删除旧属性)。这些动态变化对数据的机密性造成了非常巨大的影响，因为一旦属性发生变化，原有的访问策略会使得未授权用户获取访问权限，或者已授权用户突然失去访问权限。如果没有做好属性撤销工作，以上情况就很有可能发生并使整体的访问控制完全失控。因此，构建合理的属性撤销机制是实现安全且灵活的ABE 算法的核心。

目前相关的研究学者对ABE 撤销机制做了许多研究，但是撤销工作往往涉及巨大的计算量，甚至导致最后解密计算无比复杂，于是使得许多方案无法直接应用于PHR 系统当中，否则将会极大地降低PHR 系统的可用性。因此如何制定灵活的高效的撤销机制乃是将ABE 算法应用到PHR 系统当中的当务之急。

1.1 相关工作

Laranjo 等人[1]最早指出在未来的医疗系统将逐步发展成为一种以病人为中心的医疗系统，病人将拥有直接获取自己医疗数据的权利。他们的工作说明了未来的PHR 数据分享应当具备相当的灵活性。Chen 等人[9]指出基于云计算的PHR 系统处于一种更为开放的环境，因此不仅需要对PHR 数据进行加密，更应当允许用户自己决定谁可以获取他们的健康数据。为了实现该功能，他们提出了一种基于拉格朗日插值法的动态医疗数据访问控制算法，使得医疗数据分享在灵活性和安全性上都得到了很大的提升。Li 等人[10]根据医疗数据分享系统中用户的数据接入需求将系统划分为两个安全域:公有域与私有域。公有域包含医生、护士以及医药研究院等大多数用户，其中的PHR 数据分享采用基于多权威的密文策略属性加密算法。个人域包含与用户有个人密切关系的人，其中的PHR 数据分享采用密钥策略属性加密算法。该算法能够较好地提高PHR 数据分享的秘钥管理效率。Zhang 等人[11]设计了一种基于等级化匿名ABE 的医疗数据访问控制算法，该方案能够充分保护了用户的隐私并且有效缩小密钥的尺寸。

在属性撤销方面，Pirretti 等人[12]最早提出了一种ABE 属性撤销的方法:每个属性均包含有效期，鉴权中心周期性地释放属性的最新版本并更新所有解密者的私钥组件。该方法实现起来很简单但是存在诸多缺陷，例如有效期时长的确定缺乏现实依据、所有访问者必须保存并即时更新每个时间段的私钥。Bethencourt 等人[8]提出为解密者的每个属性设置终止日期，而在密文的访问策略里附带每个属性的时间信息。解密过程中，如果解密者属性的终止日期在时间信息之前，那么视该属性为无效属性。尽管该方法降低了密钥更新和存储的开销，但无法支持属性的即时撤销。Boldyreva 等人[13]提出一种基于二叉树的ABE 撤销机制，将KP-ABE 算法当中每个解密者关联至二叉树中的节点，同时将私钥分为由解密者保留的秘密组件以及由鉴权中心持有的向全局公开的更新组件，该机制最终使得密钥更新的数量与解密者数量呈对数关系，然而仍无法实现属性的即时撤销。在此之后，也有部分学者提出了利用密钥隔离技术[14－15](Key-Insulated Mechanism)实现ABE 属性撤销，虽然能够保证不同时间片段的前后向安全性，但是如何合理分配时间片段仍然是一个难题。Ibraimi 等人[16]在CP-ABE 算法当中引入第三方仲裁中心来掌握属性撤销列表，这使得私钥变为两部分，其中一部分私钥由仲裁者持有。解密过程中仲裁中心首先判断是否存在已被撤销的属性，若没有则使用该部分私钥完成部分解密工作，然后由用户自己完成剩余的解密工作。该算法利用仲裁中心减轻了鉴权中心的工作负担，但是必须保证仲裁者是诚实的并且始终在线。文献[17－18]均采用代理重加密技术(Proxy Re-Encryption)，利用密钥中心来标记主密钥的演化版本，由主密钥产生的公钥参数、私钥以及密文都用版本号来标记，当撤销发生时由密钥中心更新被撤销属性主密钥构件的版本号。文献[19]提出了一种密钥的协作管理机制，不仅能够避免将密钥完全托管给密钥中心而带来的信息泄露风险，而且能够防止用户密钥管理不慎所产生的密钥泄露问题。其采用了一种基于属性群[20－21]的撤销方法保证密钥的前/后向安全性，然而在重加密过程中执行的指数运算次数与属性群中用户数量呈线性关系，这就导致在执行海量属性的撤销时效率不尽如人意。值得注意的是，以上研究均采用了间接撤销的思路，即由某个机构周期性地更新用户私钥组件，只有未被撤销的用户才能获取更新的私钥，而被撤销的用户将不再获取更新的私钥。也有部分研究采用了直接撤销的思路[22－23]，但是直接撤销机制很难做到细粒度撤销，同时会增加公钥参数的长度，因此ABE 撤销机制的研究大都集中于间接撤销。

1.2 本文工作

为了解决以上问题，本文基于间接撤销思路在现有方案的基础上，对ABE 撤销方案的灵活性、安全性以及计算效率等方面进行了改进。首先提出了快速的即时撤销(fast and immediate revocation，简称FIR)算法，不需要用户保持在线以更新私钥，并使得解密时获取属性群密钥所需的乘法操作降低为仅1 次，从而在保证即时撤销的同时减少了解密开销。围绕FIR 算法设计了一种支持快速撤销的密文策略属性加密(ciphertext policy attribute-based encryption supporting fast revocation，简称CP-ABE-FR)方案，通过理论分析证明了该方案的安全性。基于以上的方案进一步构建了一种应用于PHR 系统的访问控制系统模型，实现了个人健康记录的安全加密以及灵活的访问控制。仿真实验表明，本文提出的PHR 系统访问控制模型在加解密操作时具备较高的计算效率。

2 预备知识

2.1 访问策略

定义1(访问策略，Access Policy) 设{P1，P2，…，Pn}是由若干元素组成的集合，访问策略是一组范式，它定义了一个由集合{P1，P2，…，Pn}的部分非空子集组成的集合，即A∈2{P1，P2，…，Pn}＼Ø。

若任意两个集合B和C满足B∈A并且B⊆C时，使得C∈A，那么称A 是单调访问策略。我们称集合S是关于访问策略A 的合法集合，当且仅当S∈A。否则称S为关于访问策略A 的非法集合。

2.2 线性秘密分享算法

定义2(线性秘密分享算法，Linear Secret Sharing Scheme，以下简称LSSS) 我们称关于集合P 的秘密分享算法Π在群Zp上是线性的，当且仅当其满足以下条件:

(1)集合P 中每个元素对应的分享因子都是Zp群上的一个向量；

(2)存在一个l行列m的矩阵M，我们称之为分享矩阵。同时存在函数ρ，对于分享矩阵M 的任意第i行Mi，ρ(i)将Mi映射到P 中的某个元素。设列向量v＝(s，v1，v2，…，vm)，其中s∈Zp是待分享的秘密，v1，v2，…，vm∈Zp是一组随机数。那么Mv是P 中所有元素对应的分享因子行向量，其中λi＝Miv就是元素ρ(i)的分享因子。

对于任意一种单调的访问策略A，均存在与之对应的分享矩阵M 和一个映射关系ρ的组合[21]。如果访问策略A 包含l个元素，那么分享矩阵M 的行数必定为l。此外，LSSS 算法具有如下的重构性质:假设集合S是关于访问策略A 的合法集合，我们可构建一个索引集合I⊂{1，2，…，l}使得I＝{i:ρ(i)∈S}。那么必定可以在多项式时间内找到一组元素{ωi∈Zp}i∈I，使得

2.3 双线性对

定义3(双线性对，Bilinear Pairing) 设G1和G2是两个阶为大素数p的乘法循环群，g是G1的生成元，我们称映射e:G1×G1→G2是关于G1和G2的双线性映射，当且仅当e满足以下性质:

(1)双线性:对于任意的u，v∈G1以及a，b∈Zp，都有e(ua，vb)＝e(u，v)ab；

(2)非退化性:存在生成元g，使得e(g，g)≠1，其中1 是乘法循环群G2的单位元；

(3)可计算性:对于任意的g1，g2∈G1，存在多项式时间的算法可以计算出e(g1，g2)的值。

2.4 判定双线性Diffie-Hellman 困难假设

定义4(判定双线性Diffie-Hellman 困难假设，Decisional Bilinear Diffie-Hellman Assumption，DBDH) 假设G1是一个阶为素数p的群。在已知一组参数{g，A＝ga，B＝gb，C＝gc}的情况下，敌手难以区分e(g，g)abc∈G2与另一个随机数e(g，g)z∈G2。

假设存在一个算法B 在获得参数{g，A，B，C，Z}后，输出1 表示Z＝e(g，g)abc，输出0 表示Z＝e(g，g)z。那么我们认为算法B 能够以优势ε解决DBDH 假设，当且仅当:

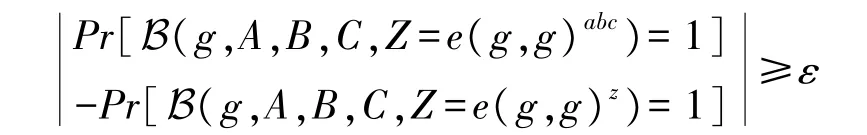
2.5 属性群

定义5(属性群，Attribute Group) 设N＝{att1，att2，…，attn}为系统的全局属性集合，U ＝{u1，u2，…，uq}为系统全体用户集合。对于任意属性attx∈N，U 当中所有拥有该属性的用户的集合称为关于属性attx的属性群，记为Gx。

我们定义G＝{G1，G2，…，Gn}为系统中所有属性群的集合，即对于任意一个属性群Gx∈G，其中所有用户共享一个关于attx的密钥Kx∈Zp，称为属性群密钥。我们定义属性群密钥集合为K ＝{K1，K2，…，Kn}。

3 方案架构

本文提出的CP-ABE-FR 方案包括初始化算法set、私钥生成算法kgen、加密算法enc、FIR 算法fir和解密算法dec五部分。方案架构的描述如下:

set(1λ)→:初始化算法输入一个安全参数1λ，输出全局的公钥PK和主密钥MSK，其中公钥PK向全网公开，而主密钥MSK则秘密保存。

kgen(S，PK，MSK)→:当收到来自用户uk的私钥生成请求后，私钥生成算法输入属性集合S、公钥PK以及主密钥MSK，最终输出与属性集合相对应的私钥SK以及一个对话公钥PKsession，k。

enc(A，PK，M)→CTinit:加密算法输入访问策略A、公钥PK以及PHR 数据明文M，输出与访问策略A 对应的初始密文CTinit。

fir(G，CTinit/CT)→:FIR 算法以一种迭代方式输入属性群集合G、初始密文CTinit或者之前的FIR 密文CT，输出全局FIR 消息头headers以及新的FIR 密文CT。

dec(t，headers，CT，SK)→Mor ⊥:解密算法输入时间戳t、全局FIR 消息头headers、FIR 密文CT以及私钥SK，在时间戳协商无误的情况下，当用户的属性集合满足访问策略时输出PHR 数据明文M，否则输出⊥表示解密失败。

基于提出的CP-ABE-FR 方案，本文构建面向PHR 系统的访问控制模型并进行了仿真实验。该访问控制模型包含以下四类角色:

(1)密钥中心:是一个可信的权威机构，负责所有解密者的权限认证和各类密钥的发布。

(2)PHR 加密者:是PHR 数据的拥有者，负责上传自己的PHR 数据并自由制定相应的访问策略。

(3)PHR 存储中心:是存储PHR 数据的媒介，所有PHR 数据都以FIR 密文的形式存储在当中。此外一旦用户的属性集合发生撤销，还将负责对相关的密文进行即时的更新。

(4)PHR 解密者:是试图获取PHR 数据的一类用户，其身份用一个属性集合来表示。解密者拥有一个与其属性集合相对应的私钥，并通过私钥来解密密文。当PHR 解密者的属性集合发生改变时，系统需要对该属性采取即时的撤销以保证前向/后向安全性。

该系统模型的工作流程如图1 所示，在系统正式启动时，密钥中心执行初始化算法产生公钥PK并发送给PHR 加密者和PHR 存储中心。当有PHR解密者提出关于某属性集合S的密钥生成请求时，密钥中心执行密钥生成算法产生与该属性集合相对应的私钥。PHR 加密者通过加密算法Encrypt使用公钥PK和访问策略A 对PHR 数据明文M进行加密生成初始密文CTinit交由PHR 存储中心存储。PHR 存储中心收到初始密文之后首次执行FIR 算法生成FIR 消息头headers和FIR 密文CT。当某个PHR 解密者撤销属性atty时，PHR 存储中心对重加密密文再次执行FIR 算法，并更新生成新的FIR 消息头headers′和FIR 密文CT′。如果PHR 解密者发出解密请求，PHR 存储中心和PHR 解密者立即协商此时的时间戳t，并执行解密算法。如果此时的属性集合满足访问策略且时间戳无误，那么解密者则顺利获取访问权限，然后解密得到PHR 数据明文。反之则无法获取任何有效信息。

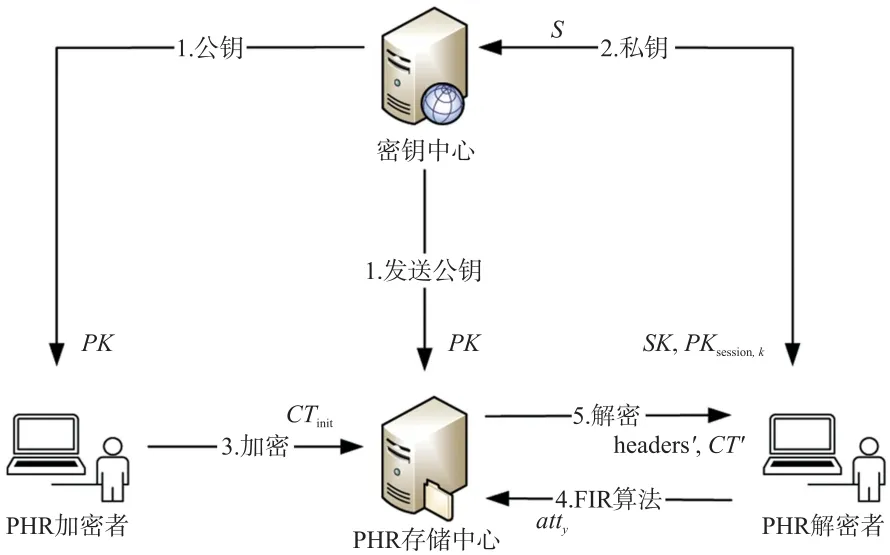
图1 PHR 系统访问控制模型流程

4 算法流程

4.1 初始化算法

设全局属性空间为N ＝{att1，att2，…，attn}，初始属性群集合为G ＝{G1，G2，…，Gn}。首先输入一个安全参数1λ，算法产生一个长度为λ比特的素数p以及两个阶为p的循环群G1和G2。设g是G1的一个生成元。然后算法生成一个双线性对映射e:G1×G1→G2、一组与属性空间N 对应的随机数{h1，h2，…，hn}以及两个抗碰撞的散列函数H:{0，1}∗×{0，1}∗→G1和H1:{0，1}∗→Zp。随后选择两个秘密的随机数α，β∈Zp，最终输出公钥:

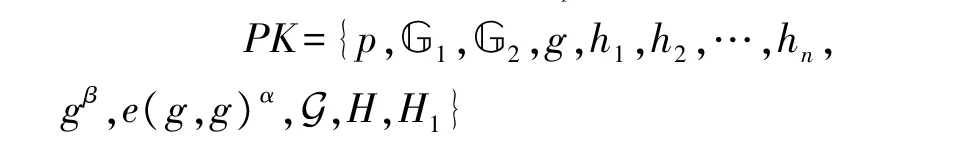
同时保留主密钥:

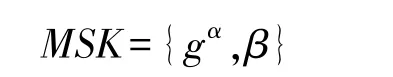
4.2 私钥生成算法

选择一个随机数τ∈Zp并计算D1＝gα＋βτ以及D2＝gτ。对于属性集合S当中的任意属性attx，计算对于任意用户uk，该用户自己选择一个秘密字符σk∈{0，1}∗，然后产生一个对话私钥SKsession，k＝H(IDk，σk)以及一个对话公钥PKsession，k＝gH(IDk，σk)，其中IDk为该用户唯一的身份标识。最后输出关于属性集合S的私钥:

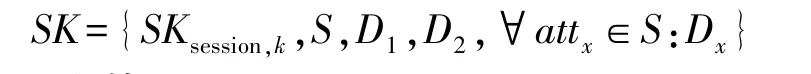
4.3 加密算法

对于一个访问策略A，记其包含的属性总数为l。加密算法首先生成对应的LSSS 访问结构(M，ρ)，其中M 是一个l行m列的矩阵，ρ为映射函数负责将矩阵的任意一行映射为访问策略里的某个属性。其次生成一个秘密数s∈Zp以及一个随机向量v＝(s，v1，v2，…，vm)，其中v1，v2，…，vm都是Zp上的随机数。然后计算C1＝M▪e(g，g)αs和C2＝gs。同时对于任意一个属性attρ(i)计算，其中λi＝Miv。最后输出初始密文:

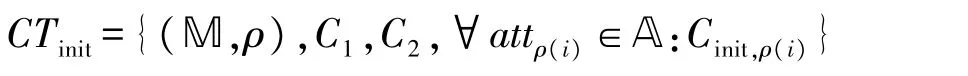
4.4 FIR 算法

基于文献[19]采用的撤销方案基础上，我们提出并采用FIR 算法优化属性撤销的过程，使得用户不需要保持在线以更新私钥。该算法执行过程如下:

如果针对某初始密文CTinit首次执行FIR 算法，通过属性群集合G ＝{G1，G2，…，Gn}的描述产生对应的属性群密钥集合K ＝{K1，K2，…，Kn}。其次选择一个秘密随机数γ∈Zp并产生对话公钥PKsession＝gγ以及对话私钥SKsession＝γ。然后计算关于任意用户uk的因子

假设任意一个属性群Gx∈G 包含的用户数量为d。对于该属性群，FIR 算法产生一个多项式fattx。随后产生一组元素{P0＝Kx＋a0，P1＝a1，…，Pd＝ad}，即关于该属性群的FIR 消息头:

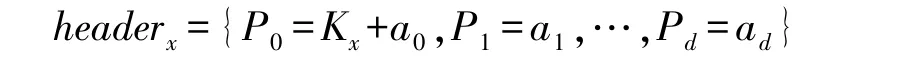
以此类推，全局的FIR 消息头为:

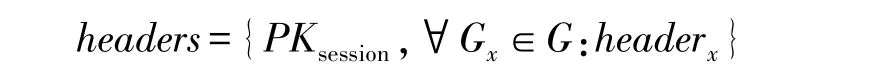
最终FIR 密文为:

当撤销某个用户的属性atty时，首先将属性群集合更新为:其中是剔除了该用户的属性群。 相应的，属性群密钥集合更新为:Kn}，其中是更新的属性群密钥。 然后中所有用户各自产生自己的随机数。 为了不失一般性，我们假设用户uk产生的新随机数为并计算新的对话公钥。 云存储中心根据新的对话私钥计算，随后产生新的多项式以生成新的FIR 消息头:

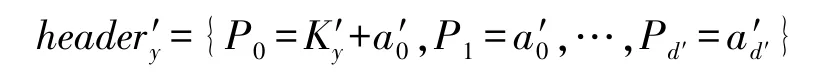
于是全局FIR 消息头将更新为:

之后所有访问策略中包含属性atty的FIR 密文将更新为:

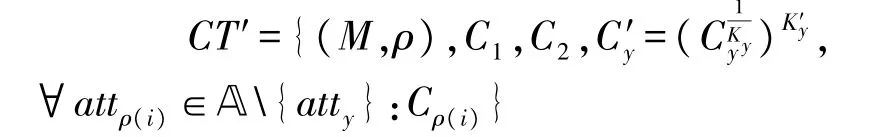
可以看到，以上的全部过程不需要用户保持在线以更新自己的私钥，从而极大提高了系统的可用性。

4.5 解密算法

在解密算法当中我们通过时间戳克服用户在更新私钥时必须保持在线的问题，使得用户不需要更新自己的私钥就可以实现属性的即时撤销，具体的执行过程如下:

当建立解密会话时，首先记录此时的时间戳t。紧接着将全局FIR 消息头更新为:

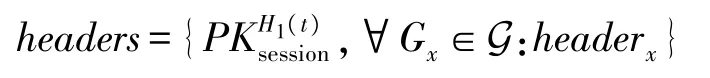
随后将更新后的全局FIR 消息头以及FIR 密文发送给用户。之后用户首先通过自己的时间戳t计算。对于任意属性attx∈S，解密算法执行如下计算获取对应的属性群密钥:

不难看出，获取属性群密钥所需的乘法操作仅需1 次。相比现有的属性群撤销方法，FIR 极大地优化了解密开销。要注意的是，如果用户非法获取了更新后的全局FIR 消息头，他将无法知道更新所用的时间戳，那么则无法获取正确的属性群密钥。

获取属性群密钥之后，解密算法执行如下计算:

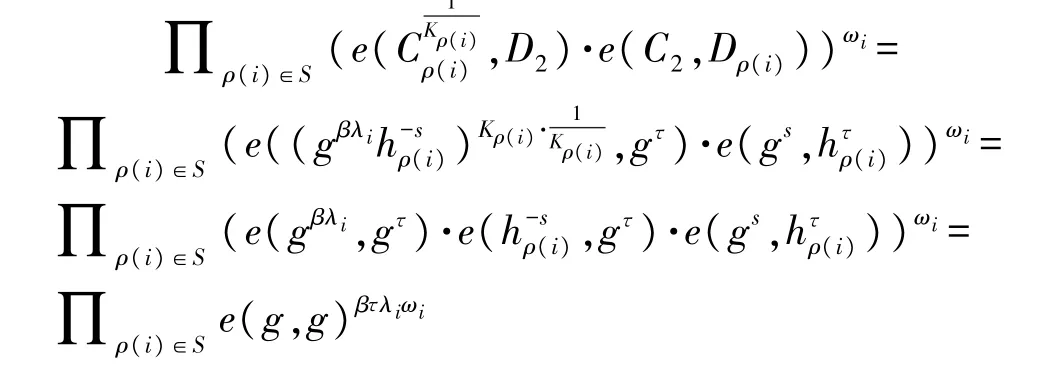
根据LSSS 性质可知，如果属性集合不满足访问策略的权限，那么将无法在多项式时间内恢复出秘密s，并导致解密失败。反之则能在多项式时间内恢复出秘密s，从而使下式成立:

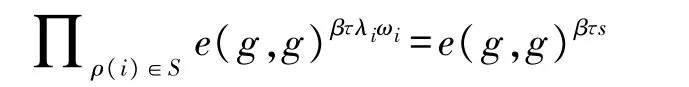
将此时得到的参数记为A，然后继续执行如下运算:

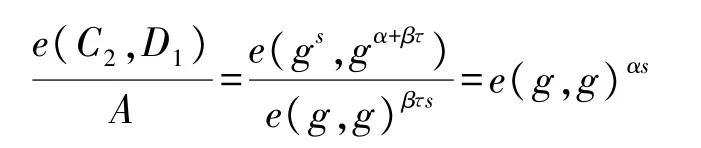
将此时得到的参数记为B，最终执行如下运算即可获取正确的消息明文:

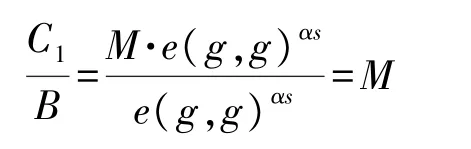
5 安全性分析

5.1 FIR 算法前/后向安全性

由以上的密文组成可以看出，对于撤销了属性atty的用户，即使其利用之前获取的消息头计算得到属性群密钥Ky也无法完成解密获取正确的消息明文，因为此时密文已被更新。因此可以保证方案的前向安全性。

对于属性集合中仍然包含属性atty或者刚刚拥有属性atty的用户，当发起解密时只能获取当前时间戳的重加密消息头和重加密密文，即使获取了过去某个时刻的消息头也无从知晓具体的会话时间是多少，所以无法抽取过去的属性群密钥。即使其已下载了过去的密文也不能正确解密。因此可以保证方案的后向安全性。

5.2 CP-ABE-FR 机密性

本文基于FIR 算法构造了CP-ABE-FR 方案，该方案的安全性建立在DBDH 困难假设的难解性之上。为方便分析，我们给出如下定理和相应的证明:

定理如果DBDH 问题是难解的，那么一定不存在多项式时间内的敌手能以不可忽略的优势破解CP-ABE-FR 方案。

证明为了证明以上的定理，我们设计一种挑战游戏，通过该游戏将CP-ABE-FR 方案的机密性规约到DBDH 问题的难解性上。该游戏由敌手A、模拟器B 以及挑战者C 共同参与完成，流程如下:

(1)初始化阶段:首先敌手A 向模拟器B 发送一个挑战访问策略A∗。其次挑战者C 产生一个循环群G1，选择该群的一个生成元g以及三个秘密数a，b，c∈Zp，并将g、A＝ga、B＝gb、C＝gc和Z发送给模拟器B。然后模拟器B 选择一个循环群G2以及一个双线对映射e:G1×G1→G2，一组秘密随机数{β，r1，r2，…，rn}、一个属性群集合G 以及两个随机预言机H:{0，1}∗×{0，1}∗→G1和H1:{0，1}∗→Zp。最后模拟器B 向敌手A 发送如下的公钥:

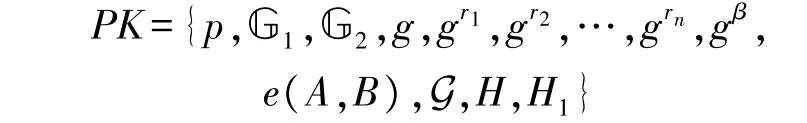
(2)询问阶段:敌手A 向模拟器B 有限次地发送如下两种询问:

(a)私钥询问:首先模拟器B 维护一个列表List。其次敌手A 在属性群集合G 中任意选择一个用户uk(记用户uk的身份表示为IDk、属性集合为S)并向模拟器B 发出关于属性集合S的私钥请求。然后模拟器B 产生随机数R1，R2，R3∈Zp，然后返回私钥:

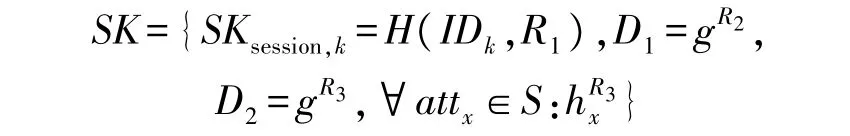
最后模拟器B 在列表List 当中添加关于用户uk的元组{IDk，S，PKsession，k＝gH(IDk，r1)，R1，R2，R3}。

(b)加密询问:首先敌手A 选择一个PHR 数据明文M以及一个访问策略A，并向模拟器B 发送关于M和A 的加密请求。其次模拟器B 首先根据属性群集合产生对应的属性群密钥集合K ＝{K1，K2，…，Kn}并生成与访问策略A 相对应的LSSS 访问结构矩阵(M，ρ)，同时选择一个秘密数s∈Zp以及一个随机向量v＝(s，v1，v2，…，vm)，计算λi＝Miv。然后模拟器B 产生如下密文给A:

同时从List 当中抽取用户的对话公钥PKsession，k并按照真实的重加密算法构造全局重加密消息头。对于不在List 当中的用户，模拟器B 调用私钥生成预言机来产生对应于该用户的元组并添加进列表List 当中。最终模拟器B 将密文和对应于此时时间戳的全局重加密消息头发送给敌手A。

(3)挑战阶段:首先敌手A 向模拟器B 提交两个长度相同的PHR 数据明文M1和M2。其次模拟器B 生成与A∗对应的LSSS 访问结构(M∗，ρ∗)以及一个随机向量v＝(s，v1，v2，…，vm)。然后对于任意属性attρ(i)∈A∗计算，其中λi＝Miv。最后模拟器B 选择一个随机的比特值δ∈{0，1}并返回如下的挑战密文给A:

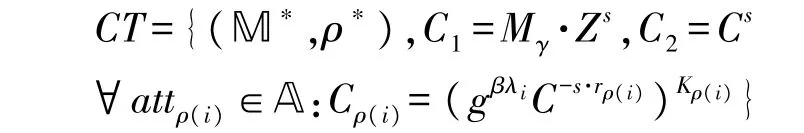
(4)询问阶段:与第2 阶段一样，敌手A 继续向模拟器B 发送有限次的私钥询问和加密询问。要注意的是，所有询问必须满足以下的限制:

(a)私钥询问过程中，所有的属性集合S都不可以满足挑战访问策略A∗；

(b)访问策略A∗或者是M1和M2不可以用来进行加密询问。

(5)猜测:敌手A 输出δ′∈{0，1}作为对δ的猜测。如果δ＝δ′则敌手A赢得挑战游戏，同时模拟器B 输出1 表示其猜测Z＝e(g，g)abc。如果δ≠δ′则敌手挑战失败，同时模拟器B 输出0 表示猜测Z＝e(g，g)z。

当Z＝e(g，g)abc时，挑战阶段的加密过程与真实CP-ABE-FR 算法的加密过程相同。假设敌手A破解CP-ABE-FR 算法的优势为ε′，那么模拟器B输出1 的概率为:

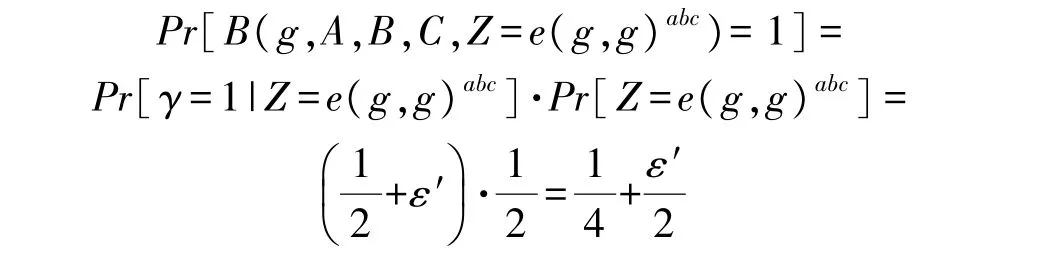
当Z＝e(g，g)z时，敌手A 所获得的挑战密文是由一个完全随机的密文，那么敌手A 的猜测是完全随机的。在这样的情况下，模拟器B 输出1 的概率为:

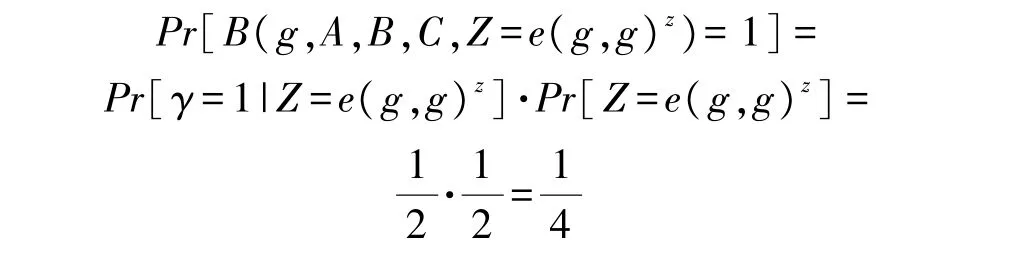
因此，模拟器B 解决DBDH 问题的优势满足:

由此可以推断，如果不存在多项式时间算法能够以不可忽略的优势ε解决DBDH 问题，那么必然不存在多项式时间敌手A 破解CP-ABE-FR 算法。所以本算法能够很好地保证机密性。

5.3 CP-ABE-FR 抗合谋攻击

合谋攻击是指多名解密者通过各自的私钥非法地产生一个全新的私钥，而这个全新的私钥却能够正确实现正确的解密。假如这么多名解密者的属性集合都不符合密文的访问策略，却能够通过合谋产生合法的私钥，那么密文的安全性将受到巨大的威胁。

在CP-ABE-FR 方案中，每产生一个私钥时算法都会生成一个不同的随机数τ，并将这个随机数嵌入到私钥组件当中，即每个私钥都有一个不同的D＝gα＋βτ。即使多名消息访问者尝试进行合谋，也无法获取一个合法的私钥，因为来自不同消息访问者的私钥组件内嵌入了不同的随机数。综上所述，CP-ABE-FR 能够很好地抵抗合谋攻击。

6 性能分析

6.1 FIR 撤销效率分析

本文在LHS 方法[19]以及Hur 方法[21]的基础上针对属性撤销过程中产生过大的计算负荷的问题进行了改进，提出了FIR 算法。为方便分析FIR 的撤销效率，我们定义Tmul以及Texp分别为生成消息头以及抽取属性群密钥时执行单次乘法或指数运算所需的时间。

比较结果如表1 所示，LHS 方法[19]以及Hur 方法[21]生成关于属性群Gx的消息头时均需要执行1次乘法运算以及2d次指数运算，而抽取属性群密钥时均需要执行d次乘法以及d(d＋3)/2 次指数运算，其中d为属性群Gx包含的用户数量。

表1 撤销效率比较

本文提出的FIR 算法在生成关于属性群Gx的消息头只需要执行1 次乘法，相比LHS 方法[19]和Hur 方法[21]减少了2d次的指数运算。同时FIR 算法在抽取对应的属性群密钥时需执行d次乘法以及d(d＋1)/2 次指数运算，相比以上两种方案减少了d次指数运算。因此FIR 算法提高了属性撤销的计算效率。

6.2 CP-ABE-FR 撤销功能分析

本节在撤销功能角度上对基于FIR 算法设计的CP-ABE-FR 方案与其他类似方案进行了比较。

比较结果如表2 所示，PTM 方法[12]、HS 方法[14]以及QLZ 方法[18]利用密钥中心来执行撤销，这使得密钥中心必须完全可信。而且由于密钥中心已经承担了公钥和私钥的发布工作，再承担撤销工作无疑将增加了其本身的计算负荷。IPN 方法[16]和YWR 方法[17]的方案利用第三方的仲裁中心执行撤销，虽然分担了密钥中心的负荷，但是仲裁中心必须要保持完全可信。本文提出的CP-ABE-FR 利用现有的密文存储中心执行撤销工作，其可信程度只需要保持半可信就可以保证撤销工作的安全性。除此之外不需要用户保持实时在线更新私钥，同时又可以实现即时撤销。因此在撤销功能上，本文提出的方案较其他方案而言有显著改进。

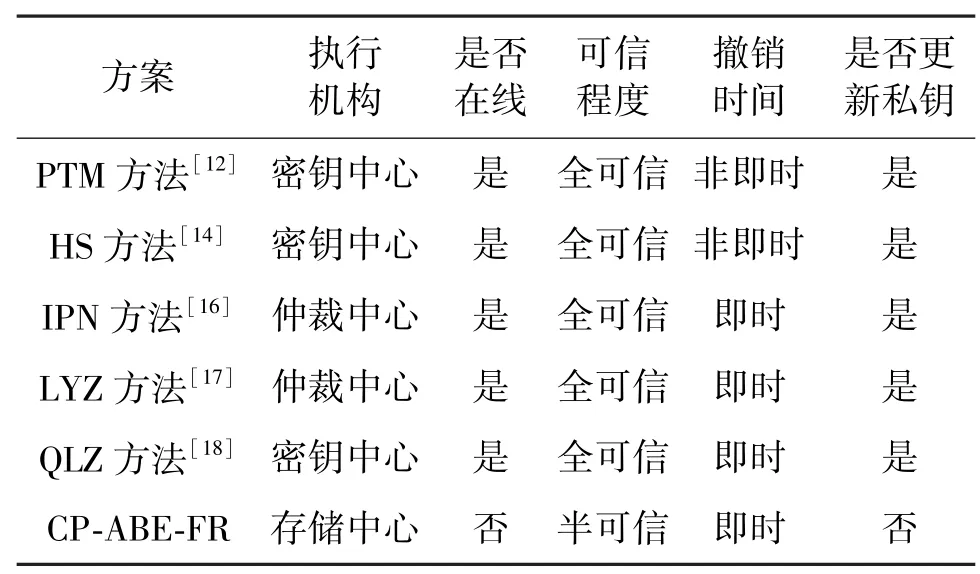
表2 撤销功能比较

6.3 仿真实验

本系统的仿真硬件为Intel(R)Core(TM)i5－4200H CPU ＠ 2.8GHz，内存为4GB，系统为Windows 10，所使用代码库为JPBC2.0，实验基于512 位的椭圆曲线，曲线的阶为120 bit 的大素数。实验分别基于LHS 方法[19]、Hur 方法[21]以及本文所提出方案构建了PHR 系统访问控制模型，并记录了在不同的属性数量情况下的平均加解密计算时间。

几种系统模型在不同属性个数情况下的平均加密时间如图2 所示。LHS 方法[19]和Hur 方法[21]都支持基于属性群的细粒度即时撤销，因此在加密过程中都需要对密文再次加密。Hur 方法[21]的加密时间整体上稍短于LHS 方法[19]的方案，而基于CPABE-FR 的PHR 系统访问控制模型尽管增加了FIR算法，但是FIR 算法本身并没有给系统的加密工作产生太大的计算负荷。

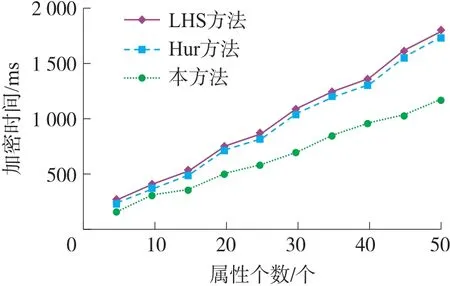
图2 平均加密时间对比

同样地，平均解密时间的统计如图3 所示。LHS 方法[19]和Hur 方法[21]所需的解密时间相当，但是LHS 方法[19]采用了分布式的私钥进行解密，所以总体上解密时间稍长。而CP-ABE-FR 则将PHR 解密时间降低了约9.3%。因此总体来说，本文所提出的PHR 系统访问控制模型的解密计算效率是比较可观的。

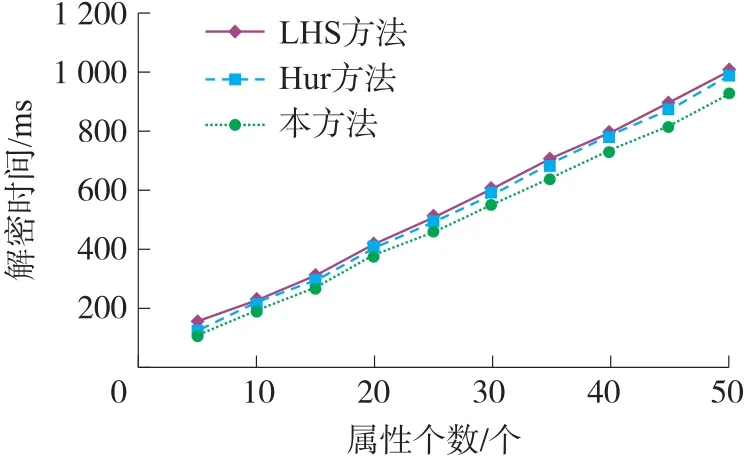
图3 平均解密时间对比

7 结束语

个人健康记录云作为云计算的延伸服务，既需要提供安全的数据保护，也需要支持灵活的访问权限控制。ABE 算法能够满足个人健康记录云的安全需求，但是现有ABE 算法往往依赖大量的计算才能保证在属性撤销的前/后向安全。本文在ABE 算法的基础上提出了一种快速的即时撤销算法，使得用户不需要在线更新私钥就可以实现快速的、即时的撤销，同时降低了撤销的计算开销。理论证明该方法能够保证PHR 数据的安全性。仿真实验表明，基于本方法构建的PHR 系统访问控制模型具备较高的加解密计算效率。在算法的计算效率上可以做进一步的改善，比如预计算、外包计算思路缩短解密时间，这将是下一步的研究方向。