基于分层极限学习机的锂离子电池剩余使用寿命预测∗

史永胜，洪元涛，丁恩松，施梦琢，欧 阳

(1.陕西科技大学电气与控制工程学院，陕西 西安 710021；2.江苏润寅石墨烯科技有限公司，江苏 扬州 225600)

锂离子电池的剩余使用寿命(Remaining Useful Life，RUL)在电池管理系统中的重要性正在逐渐凸显出来。当前对于锂离子电池RUL 的预测方法越来越多，总体分为两类:基于模型的方法和数据驱动的方法。基于模型法的主流模型有电化学模型、等效电路模型和数学模型等。Liu 等人[1]基于容量衰减的电化学模型，提出了一种改进的锂离子电池退化模型。然后利用粒子滤波跟踪模型参数和状态的变化实现对RUL 的预测。等效电路模型利用电子元件组成的电路网络来等效电池的电气特性，已被广泛用于电池状态的估计[2]。Guha 等人[3]基于分数阶等效电路模型(FOECM)得到锂离子电池的电化学阻抗谱(EIS)，然后将EIS 代入粒子滤波框架中的回归模型预测出电池的RUL。这类方法依赖准确而复杂的电池容量退化模型，增加了建模难度和计算复杂度[4]。另一类利用大数据预测电池RUL 的方法并不需要电池内部详细的老化机理，因此这类方法在研究预测问题上逐渐受到关注[5]。基于数据驱动的方法通常使用监测数据来拟合变量退化模型，并通过将变量外推到故障阈值来计算RUL。韦海燕等[6]通过将电池的容量数据作为新陈代谢灰色粒子滤波(MGM-PF)算法的输入来进行电池RUL 的预测。庞晓琼等[7]提出了一种结合主成分分析(PCA)特征融合与非线性自回归(NARX)神经网络的锂离子电池RUL 间接预测框架，并结合实验数据验证了该框架的较强适用性。

上述方法在对电池RUL 预测时，主要利用已经循环老化后的电池特征数据结合失效阈值来判断电池是否达到寿命终止(end of life，EOL)，其本质只是对于电池当前剩余使用容量的一个估算，并没有实现真正意义上的RUL 提前预测。而且大部分文献的电池数据集相对较小，因此基于这些数据的预测结果并不具有代表性。

针对以上问题，本文提出了基于分层极限学习机的锂离子电池剩余使用寿命预测模型。首先在数据集的选取方面，采用了丰田研究所的超大数据集，保证了基于大数据下的预测结果的泛化性能。其次针对大数据的数据处理方法，选择了基于ELM 的稀疏自动编码器进行降维和特征提取工作，缩减了大数据处理的时间并提高了预测算法的效率。最后把稀疏自动编码器与原始ELM 相结合形成分层极限学习机H-ELM，通过对电池容量退化前期的少量循环数据进行训练，最终实现对电池RUL 的提前准确预测。

1 分层极限学习机H-ELM 的建立

1.1 极限学习机ELM 算法

假设具有L个隐层节点的单隐含层前馈神经网络(SLFN)可以用下式表示:

式中:Gi(▪)表示第i个隐层节点的激活函数，ai是将输入层连接到第i个隐含层的输入权重向量，bi是第i个隐含层的偏置权重，βi是输出权重向量。对于具有激活函数g的隐层节点，Gi定义如下:

文献[8]证明，即使隐层节点的参数被随机初始化，SLFN 也可以逼近任意紧凑子集X∈Rd上的任何连续目标函数。因此可以使用随机初始化的隐层节点构建ELM。给定训练集{(xi，ti)｜xi∈Rd，ti∈Rm，i＝1，…，N}，其中xi是训练数据向量，ti表示每个样本的目标，L表示隐藏的节点数。从学习的角度来看，与传统的学习算法不同，ELM 理论旨在达到最小的训练误差，但也要达到最小的输出权重范数

式中:σ1>0，σ2>0，u，v＝0，(1/2)，1，2，…，＋∞，λ是用户指定的参数，为了在最小训练误差和最小输出权重之间提供折中，H表示隐含层的输出矩阵

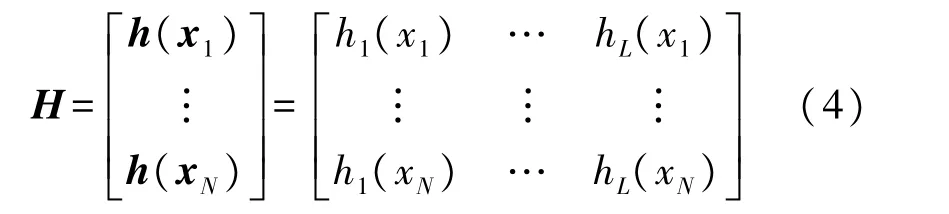
T表示训练数据的目标矩阵

ELM 训练算法可以总结如下。

(1)随机初始化隐层节点的输入权重ai和偏置bi，i＝1，…，L。

(2)计算隐含层输出矩阵H。

(3)获得输出权重向量

式中:H∗是矩阵H的Moore-Penrose 广义逆。

由岭回归理论可知，当求解输出权重β时，可以在HTH或HHT的对角线上填入正值(1/λ)。这样所得的解决方案等效于σ1＝σ2＝u＝v＝2 的ELM优化解决方案，它更稳定并且具有更好的泛化性能。也就是说，为了提高ELM 的稳定性，我们可以使

ELM 的对应输出函数为

或者我们可以使

ELM 的对应输出函数为

1.2 ELM 稀疏自动编码器

自动编码器通过将误差趋于零使编码后的输出来近似原始输入。使用随机映射输出作为潜在表示，可以很容易地构建基于ELM 的自动编码器[9]。由于ELM 自动编码器提取的特征往往比较密集，可能存在冗余，在这种情况下最好使用更稀疏的解决方案。

本文利用ELM 的普遍逼近能力进行自动编码器的设计，并在自动编码器优化的基础上加入稀疏约束，因此将其称为ELM 稀疏自动编码器。ELM稀疏自动编码器的数学表达式是

式中:X是输入矩阵，H是隐层输出矩阵，β是隐含层权重。随机映射不仅有助于提高训练时间，而且有助于提高学习精度。

为了清晰地描述l1正则化的优化算法，我们将对象函数重写为

式中:p(β)＝‖Hβ－X‖2，并且q(β)＝‖β‖l1是训练模式的l1惩罚项。

采用快速迭代收缩阈值算法(FISTA)来解决优化问题。FISTA 最小化了一个复杂度为O(1/j2)的光滑凸函数，其中j表示迭代次数。通过迭代计算，使用所得的β作为稀疏自动编码器的权重，由于采用自动编码器作为所提出的H-ELM 的结构，因此可以通过逐层比较来生成更高级别的特征表示。

1.3 H-ELM 框架

所提出的H-ELM 以多层方式构建，与传统的深度学习框架[10]的贪婪分层训练不同，H-ELM 训练体系在结构上分为两个独立的阶段:无监督的分层特征表示和有监督的特征训练。在无监督阶段，每一个隐含层的输出都能用下式计算:

式中:Hi是第i层的输出(i∈[1，K])，Hi－1是第(i－1)层的输出，g(▪)表示隐含层的激活函数，并且β代表输出权重。随着层数的增加，产生的特性变得更加紧凑。一旦前一隐含层的特征被提取出来，当前隐含层的权值或参数就会固定，不需要进行微调。

在H-ELM 中经过K层的无监督训练后，输出结果HK可以看作是从输入数据中提取的高级特征。把这些高级特征进行随机扰动以便提高模型的普遍逼近能力，然后输入到原始ELM 模型中去，最终得到H-ELM 网络的输出结果。

2 基于H-ELM 的RUL 预测模型

2.1 电池的循环数据

本文使用的电池循环数据来自麻省理工学院、斯坦福大学和丰田研究所(Toyota Research Institute，TRI)合作完成的大型数据集[11]。整个数据集包括124 块商用磷酸铁锂(LFP)/石墨电池，这些锂离子电池全部是由A123 Systems 公司生产的，其型号为APR18650M1A。电池的标称容量为1.1 Ah，标称电压为3.3 V。在30 ℃的恒温室中，将这些电池放入具有48 个通道的Arbin LBT 电池测试系统中进行充放电循环。

此数据集中的所有电池都使用一步或两步快速充电策略进行充电，一共设计了72 种不同的充电策略。每种充电策略的格式为C1(Q1)－C2，其中C1和C2分别是第一步和第二步恒流充电倍率，C1，C2∈[3.6C，6C]，Q1是电流切换时的荷电状态SOC，Q1∈[0，80%]。每个电池循环到剩余可用最大容量为0.88 Ah 时实验停止，具体的充放电循环8 步总结如下:

(1)以充电倍率C1恒流充电至电池SOC 达到Q1；

(2)以充电倍率C2恒流充电至电池SOC 达到80%；

(3)静置一段时间；

(4)以1 C 倍率恒流充电至上截止电压3.6 V；

(5)以3.6 V 恒压充电至截止电流；

(6)以放电倍率4 C 恒流放电至下截止电压2.0 V；

(7)以2.0 V 恒压放电至截止电流；

(8)静置一段时间。

电池的内阻测量是在电池充电至SOC 达到80%时，通过平均10 个±3.6 C 的红外脉冲测量内阻。数据集分为三个批次，三批实验的时间跨度长达近一年之久，每个批次的不同点见表1。

表1 三批实验数据的差异

通过改变充电条件，生成了一个包含约96 700个周期的数据集，其数据容量大小共计7.7GB。该数据集获得了大范围的循环寿命，从150 个周期到2 300 个周期不等，平均循环寿命为806 次，标准偏差为377 次。

2.2 H-ELM 的输入输出参数

为了得到较好的预测结果，依照文献[11]中的内容，在选取H-ELM 模型的输入参数时需要考虑输入参数与电池循环寿命之间的相关性，尽量选择具有高相关系数的参数，下面分别讨论不同参数与循环寿命之间的相关性。如图1 所示，绘制出124 个电池在前1 000 次循环中的容量衰减曲线。

图1 LFP/石墨电池前1 000 次循环的放电容量

在图1 中每条曲线的灰度深浅都是由电池的循环寿命决定的，即循环寿命越长对应的放电容量曲线颜色越深，循环寿命越短曲线颜色越浅。容量衰减曲线的交叉表明了初始容量与循环寿命之间的相关性较弱。针对图中前100 次循环的放电容量曲线可以发现到第100 次循环时循环寿命还没有一个明显的区分。计算出第100 次循环与第2 次循环时放电容量的比率，并把对应区间的电池数量进行统计，然后作出如图2 所示的柱形图。

图2 第100 次与第2 次循环放电容量之比的直方图

如图2 所示虚线表示比率为1.00，而且大部分电池都在比率为1 附近，因此可以看出第100 次循环的放电容量相比第2 次并没有多大变化。大多数电池在第100 次循环时的容量略高，容量的微小增加是由于存储在负极区域的电荷超过了正极[12－13]。本文继续将每个电池在第2、100 次循环时的放电容量以及第95 次～100 次循环的放电容量曲线的斜率作为自变量，循环寿命的对数作为因变量，分别作出如图3 所示的3 幅图用来探究彼此之间的关系。

通过图3 可以发现，在第2 次循环(相关系数为－0.061)和第100 次循环(相关系数为0.27)，以及在第100 次循环附近(相关系数为0.47)，循环寿命的对数和容量衰减之间存在微弱的相关性。这些微弱的相关性是可以预料到的，因为在这些早期循环中，容量退化是可以忽略的。

图3 不同循环时放电容量与循环寿命的相关性

由于基于容量衰减曲线的预测能力有限，为了得到更加全面详细的电池特征参数，本文选取了更多相关性高的输入参数变量。包括ΔQ100－10(V)的对数方差[14－15]，放电过程特征信息，充电时间，电池温度和内阻等一共9 个循环特征，并将它们作为H-ELM 模型的输入参数。下面对这9 个参数分别进行介绍。

(1)第100 次循环与第10 次循环放电容量之差的最小值

如图4 所示是电池的第100 和第10 次循环的放电容量曲线，对于124 个电池，第100 次循环和第10 次循环之间的放电容量曲线差值是电压的函数ΔQ100－10(V)，计算如下。

图4 循环容量之差

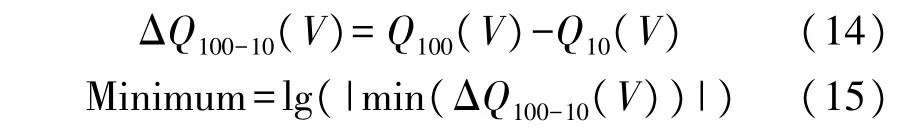
(2)第100 次循环与第10 次循环放电容量之差的方差

如图5 所示在对数坐标轴上绘制出循环寿命和ΔQ100－10(V)方差的函数，相关系数为－0.93，可见在循环寿命和基于ΔQ100－10(V)的方差之间出现了明确的趋势，计算如下。

图5 基于前100 次循环电压容量曲线的高性能特征

式中:p是电压区间2.0 到3.5 V 之间的等分数，这里取p＝1000。

(3)第2 次到第100 次循环容量衰减曲线的线性拟合的斜率

(4)第2 次到第100 次循环容量衰减曲线的线性拟合的截距

(5)第2 次循环的放电容量

(6)前5 次循环的平均充电时间

(7)第2 次到第100 次循环温度随时间的积分

(8)第2 次到第100 次循环电池内阻的最小值

(9)第100 次和第2 次循环电池内阻的差值

在确定了9 个输入参数后，将每个电池的循环寿命作为H-ELM 预测模型的最终输出。

2.3 H-ELM 预测模型的结构

在选择好模型的输入输出变量之后，本文给出了预测模型的结构框图如图6 所示。

从图6 可以看出，输入变量先经过H-ELM 的前一层即基于ELM 的多层稀疏自动编码器，目的是对输入数据进行降维处理并且提取最有价值的特征。然后把新生成的特征再加载到后一层的原始ELM中，利用ELM 的快速学习能力等优势，最终输出锂离子电池的剩余使用寿命。

图6 基于H-ELM 的电池RUL 预测模型

3 预测实验与结果分析

本文的预测算法和结果图均在MATLAB2019a中实现。数据集一共包括124 个电池，随机选取103 个电池的前100 个周期的实验数据作为训练集，剩余21 个电池数据用作测试集。在经过103 个电池数据的训练之后，H-ELM 模型对于测试集的预测结果以及误差分别如图7 和图8 所示。

图7 测试集电池循环寿命预测结果图

根据图7 可以看出H-ELM 对于测试集电池循环寿命的预测取得了较好的效果，其中大部分电池都实现了较高精度的预测，循环寿命的预测值和实际值之间相差较小。图8 展示了测试集每个电池循环寿命预测值的相对误差，在21 个电池当中有17个电池即80%的电池相对误差都小于15%，进一步证实了H-ELM 对于电池循环寿命预测的有效性。由于目前利用电池前期循环数据去预测寿命的研究还相对较少，因此本文选取了均方根误差RMSE 和平均绝对百分比误差MAPE 两项评价指标，将HELM 的预测结果与文献[7]中线性模型的结果进行比较分析，具体结果如表2 所示。

表2 两种方法的比较

通过表2 可以明显地看出H-ELM 预测模型两项指标均优于文献[7]的方法，并且其均方根误差占据较大优势。值得注意的是，尽管本文提出的HELM 预测模型在MAPE 方面性能有所提升，但是只降低了0.56%。为了验证H-ELM 预测模型的泛化性能和稳定性，本文随机挑选出测试集中的第5 号电池(循环寿命为989 次)继续利用H-ELM 进行了100 次预测实验，并将每次的预测结果进行统计，最终绘制出如图9 所示的预测结果分布直方图。

图9 测试集中第5 个电池的预测结果直方图

在图9 中，对测试集中的5 号电池循环数据应用H-ELM 模型进行了100 次预测实验，预测的循环次数结果中最小值为776 次，最大值为1 088 次。从图中可以看出，将整个预测结果平均划分为11 个小区间，每个区间长度大概为28，在包含电池实际循环次数989 次的区间[975，1 003]中有16 次预测结果落在其中。也就是说，有16%的预测结果都在绝对误差小于28/2 即14 次的误差范围内，同理有16%的预测结果的相对误差都小于14/989 即1.4%。进一步地扩大误差范围可以得到如表3 所示的统计结果。

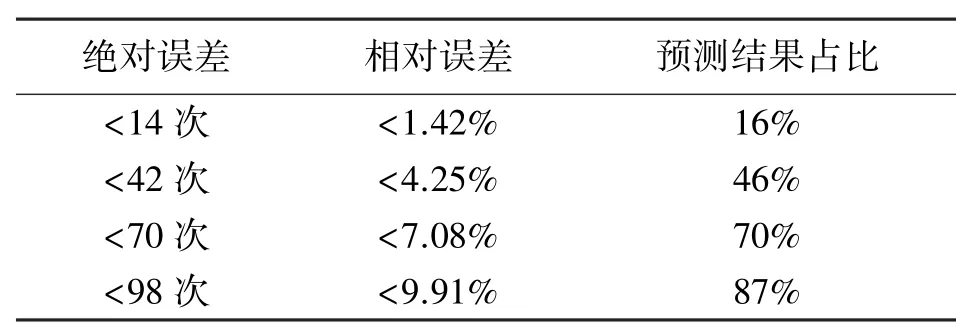
表3 误差范围对应预测结果占比

对这100 次预测实验的结果进行概率分布统计，得到如图10 所示的概率分布曲线图。

图10 第5 号电池预测结果的概率分布图

如图10 所示，概率分布曲线的峰值在电池的实际循环次数989 处，并且大概率部分都集中在989附近，由此可以看出H-ELM 模型的预测结果比较稳定，泛化性能较好，可以很好地应用于实际。

4 结论

本文在对124 个电池的大量数据的处理基础之上，应用了更加高级的H-ELM 算法，通过构建HELM 预测模型实现对锂离子电池循环寿命的提前精准预测，主要有以下两点结论:

(1)基于H-ELM 算法的预测模型可以对输入数据进行降维和特征重组优化，在面向大数据应用方面，提高了数据处理的效率。

(2)根据电池前期的少量循环数据就可以准确地提前预测出其循环寿命，预测结果的MAPE 只有10.14%，并且在针对同一电池的多次实验中表现出较好的稳定性，这将为电池的出厂检测和新电池的研发测试节省大量时间。