基于多元优化算法和DS证据理论的电力缺陷等级确定方法∗

高 莲，程宏伟，于 虹，李 鹏∗

(1.云南大学信息学院，云南 昆明 650500；2.云南电网有限责任公司电力科学研究院，云南 昆明 650500)

由于经济社会发展的需要，智能电网的建设得到充分发展，其在日常运行和维护过程中产生了大量的图像、视频、音频、文本等非结构化数据[1－2]。其中电力缺陷描述(以下简称“缺陷描述”)蕴藏着丰富的电力设备健康状况信息，基于其对缺陷等级进行有效准确划分有助于合理地安排设备检修维护，对电网的安全稳定运行有重要意义。当前缺陷等级由运维人员根据电力设备主要部件和对应现象组成的缺陷等级确定标准划分为其他、一般、紧急、重大四个等级[3－4]，但复杂多样的具体情况使定级准确性因人而异[5]，更无法保证电力缺陷等级确定的一致性。

针对运维人员基于缺陷描述信息进行等级划分时准确性和一致性无法保障的问题，近年来国内外学者进行了一系列的研究。文献[6－7]分别采用粗糙集和分层方法对电网自动生成的具有很强规范性的设备运行信息进行研究，但仍需要调度运维人员依据经验对其进行审核，具有一定的主观性；文献[8－9]分别采用C5 树和LSTM 方法对群众反映的专业词汇较少，较易理解的口语化缺陷描述进行分析，对于专业词汇较多较为复杂的电力缺陷描述文本无法适用，且算法参数由研究人员依据经验直接给出，无法实现缺陷等级的自动确定；文献[10－11]中使用K 最近邻算法(k-nearest neighbor，KNN)进行缺陷描述的等级确定，但等级划分准确性与K 的取值密切相关；文献[12]中使用卷积神经网络对缺陷描述进行等级确定，但卷积神经网络层数的不同选择使多次等级划分的结果具有一定差异。

为提高缺陷等级划分的准确性和一致性，本文提出了一种基于多元优化算法(multi-variant optimization algorithm，MOA)及DS(Dempster-Shafer)证据理论的电力缺陷等级自动确定方法，并将其用于5 863 条西南某地区电网公司变压器缺陷描述及表征电力设备运行状态的红绿灯信息。实验首先将上述数据按照4:1 的比例随机分为训练集和测试集，其次基于缺陷定级标准[4]和常用缺陷用语[13]建立的变压器缺陷描述分词词库使用结巴算法对所有变压器缺陷描述进行分词，并使用word2vec 和词频－逆文档频率算法(term frequency-inverse document frequency，TF-IDF)得到缺陷描述的向量特征表达，同时分析训练集红绿灯信息和与其一一对应的初始缺陷等级建立灯色缺陷等级辨识对应权值表并基于此表将实验数据中所有红绿灯信息向量化；然后，使用MOA 算法对预处理后的训练集在不同局部搜索半径下自动进行等级判定，寻找判别准确率较高的最优搜索半径区间，并在此区间内对测试集进行缺陷等级自动确定；最后，使用DS 证据理论决策融合测试集在最优搜索半径区间内的50 次MOA 判别结果，达到提高自动判别准确率的目的。

1 基于MOA 算法和DS 证据理论的电力设备缺陷等级确定方法

为提高电力设备缺陷等级划分的准确性和一致性，本文提出了基于MOA 算法和DS 证据理论的电力缺陷等级自动确定方法。该方法利用MOA 算法全局和局部交替探索的特性获得判别准确率较高的最优搜索半径区间，并使用DS 证据理论决策融合测试集的50 次判别结果，方法流程如图1 所示，详细过程阐述如下。

图1 MOA 和DS 证据理论等级自动确定方法流程

1.1 数据预处理

1.1.1 缺陷描述预处理

中文电力缺陷描述信息预处理的主要目的是剔除其中包含的地名、助词等冗余项并向量化保留的有用信息，使其成为自动等级确定的有效输入数据。由于缺陷描述大多为语言精简的单句短文本，预处理时无需对其进行分段、分句操作，仅需进行分词、去停用词和文本向量化[14－15]处理，各步骤详细说明如下。

(1)分词和去停用词。这一步为缺陷描述预处理的基础和关键，其主要目的是将缺陷描述合理切分成不同的词语序列并去除无用的地名和虚词。本文采用结巴算法对文本进行分词处理，在此过程中，由于电力设备缺陷描述的专业性，为提高分词的准确性，本文根据缺陷定级标准[4]和常用缺陷用语[13]建立的变压器缺陷描述分词词库，如表1 所示。同时对“哈工大停用词库”、“中科院停用词表”和电力设备缺陷描述中的地名聚合去重，构建停用词表，去除出现频率较高但对等级确定没有作用的冗余项，实现数据清理，以便后续特征选取，部分变压器缺陷描述分词结果如表2 所示。

表1 变压器缺陷描述分词词库

表2 变压器缺陷描述分词结果

(2)词向量获取。词向量获取目前有词袋模型和分布式文本表示两种。由于词袋模型未考虑词语之间的联系且存在稀疏过高的问题，因此，本文利用训练集选取分布式文本表示的word2vec 中Skipgram 模型实现词向量[16]，使用Python 中gensim 包的默认值并经过测试构建维度为50 的词向量表，然后通过查表的方式匹配缺陷描述文本中的词得出词向量，对于词向量表中没有出现的词汇，在区间[－1，1]内随机设置初始值[17]。

(3)基于词向量的文本特征表达。当前，基于词向量的文本特征表达有词模型均值和结合TFIDF 加权两种方式，文献[18]通过实验验证了加权表达的有效性。因此，本文使用TF-IDF 对重要词特征向量进行加权，增强其在特征表达中的重要性，TF-IDF 算法公式如式(1)所示:

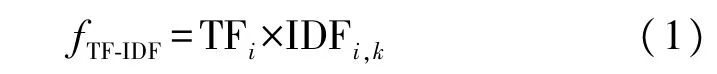
式中:TFi表示特征词i在一种等级下出现的次数占全部等级下出现次数的比例，反映特征词i在不同等级间的权重，其表达式如式(2)所示:

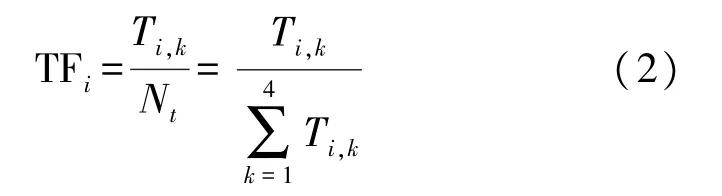
式中:Ti，k表示特征词i在等级k中出现的次数，Nt表示特征词i在四种等级中出现的次数和。

IDFi，k表示等级k中包含特征词i的文本数量占等级k全部文本数量的比例，反映同一等级下特征词i的权重，其表达式如式(3)所示:

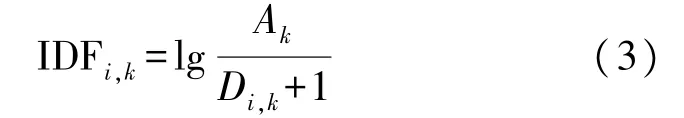
式中:Ak表示等级k的文本总数，Di，k表示等级k中包含特征词i的文本数，分母加1 避免出现0 的情况。

例如分别选取缺陷等级为一般、紧急、重大、其他的变压器缺陷描述各50 条，即四种等级下Ak值均为50，且四种等级下出现“熔断”一词的次数Ti，k分别对应为8、15、33、0，四种等级中出现“熔断”一词的条数Di，k分别对应为6、15、30、0，按照式(2)可知Nt的值为四种等级下出现熔断一词的次数Ti，k之和，即56。因此可由式(2)和式(3)计算得出TFi和IDFi，k的值分别对应为0.14、0.27、0.59、0；0.85、0.49、0.21、1.70。根据式(1)可以得出特征词权重分别为0.119、0.132、0.124、0。

1.1.2 红绿灯信息预处理

电网红绿灯信息中蕴含着电力设备运行的健康状态信息，可作为设备缺陷等级自动确定的有益补充数据。为此，对4 743 条训练样本红绿灯信息及其对应的初始缺陷等级进行分析，获得灯色与缺陷等级的最优对应关系，并以此建立灯色缺陷等级辨识对应权值表作为实验数据中所有灯色信息向量化的依据。训练样本中4 743 条灯色信息在初始缺陷等级中的占比如表3 所示。

表3 各色灯在初始缺陷等级中的分布比例

为更加直观的看到训练样本中灯色和与其一一对应的初始缺陷等级间的关系，将表3 中的数据可视化处理，得到如图2 所示的圆环图。

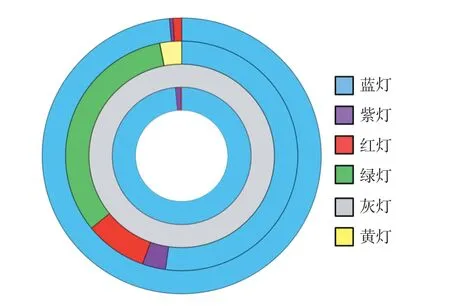
图2 四种等级下灯色占比

图2 中从内到外四个圆环依次对应训练样本中紧急、其他、一般和重大四个等级。从中可以看出蓝灯在紧急、一般和重大等级中均占有较大比例，无法与单一缺陷等级形成较好对应，因此首先使用谱系图和平均轮廓系数分析除蓝灯以外的各色灯与初始缺陷等级间的关系，得到最佳的灯色缺陷等级对应并赋予权值；然后单独对蓝灯进行分析，得到蓝灯的缺陷等级权值；最后依据上述两步得到灯色缺陷等级权值构建完整的灯色权值表并作为实验数据中各色灯的量化依据，详细步骤如下。

首先，根据除蓝灯外各灯色在初始缺陷等级中的占比构建样本集[19]作为谱系图分析的依据，样本集如表4 所示。

根据表4 所示样本集，采用组内联结法绘制如图3 所示的谱系图。

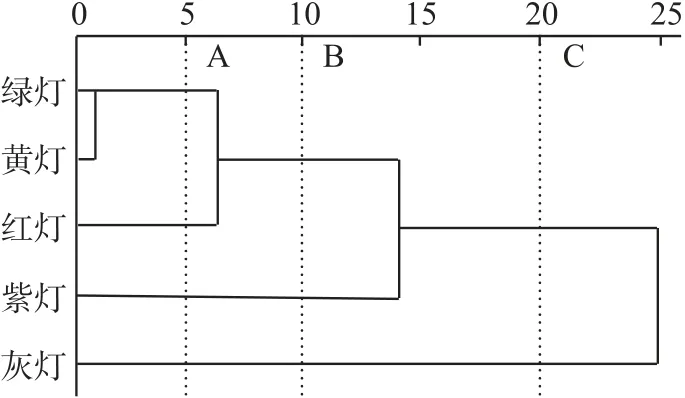
图3 组内联结法谱系图

表4 红绿灯样本集

由图3 所示，从右往左依次做C、B、A 三条截断线，由截断线C 可以看出5 种颜色的灯可分为两类{灰灯；紫灯、红灯、绿灯、黄灯}；由截断线B 可以看出5 种颜色的灯可分为三类{灰灯；紫灯；红灯、绿灯、黄灯}；由截断线A 可以看出5 种颜色的灯可分为四类{灰灯；紫灯；红灯；绿灯、黄灯}。

为确定除蓝灯外5 种颜色灯的最佳类别数，本文使用轮廓系数法评估5 种颜色灯不同类别数的合理性，并选取平均轮廓系数最大即类别数最为合理的值作为评估结果。因此，分别计算类别数为2、3、4 的轮廓系数如图4(a)～4(c)所示，并对其分别计算平均轮廓系数构建如图4(d)所示的平均轮廓系数曲线图。

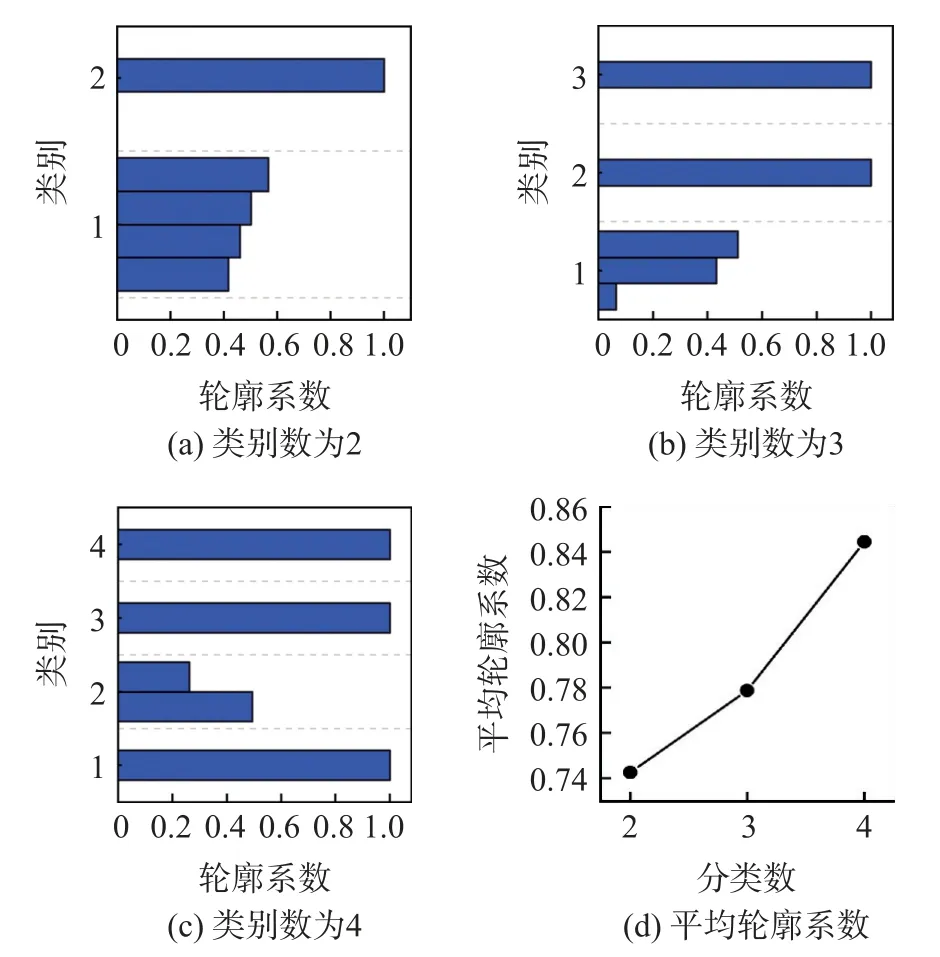
图4 不同类别数下轮廓系数图

从图4(d)可见，当分类数为4 时，平均轮廓系数最大，可以实现灯色与缺陷等级的最佳对应。结合表4，除蓝灯外的各色灯对应效果如下:灰灯只出现在其他等级中对应缺陷等级中的其他；紫灯在紧急等级中的占比较高对应缺陷等级中的紧急；红灯在重大等级中的占比较高对应缺陷等级中的重大；绿灯和黄灯只出现在一般等级中对应缺陷等级中的一般。由此建立权值分布在[0，1]之间的灯色缺陷等级辨识对应关系，用以区分灯色不同。然后，虑到蓝灯在紧急、一般、重大中均有较高占比及其自身的不可或缺性，因此赋予蓝灯中间权值0.5，以区分其他灯色。最后，根据上述分析建立如表5 所示的灯色缺陷等级辨识对应权值表，作为实验数据中红绿灯信息的量化依据。

表5 灯色缺陷等级辨识对应权值表

1.2 基于MOA 算法的电力缺陷等级确定

MOA 算法是一种有效的动静态条件下多模态算法，可在动态条件下对多模态聚类问题进行有效解决[20]，因此适合于电力设备缺陷等级的确定。通过MOA 算法确定电力设备缺陷等级时，首先根据算法的基本思想构建全局和局部搜索元；然后随机确定全局搜索元的初始聚类中心，并使用局部搜索元在全局搜索元附近探索，寻找最优的适应度函数值即类内距离尽可能小但类间距离尽可能大的聚类中心；此后重复上述步骤，获得新的聚类结果，并与上一轮聚类过程的适应度函数进行比较，保留适应度函数最优的结果，直到适应度函数变化较小或达到最大循环次数后，电力设备缺陷数据聚类完成。

为保证聚类的准确性，构造如式(4)所示的适应度函数:

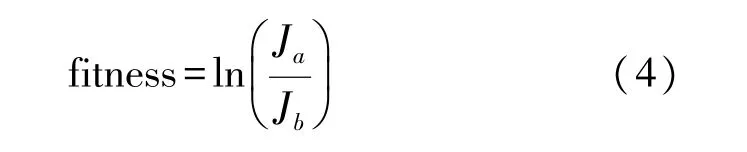
式中:

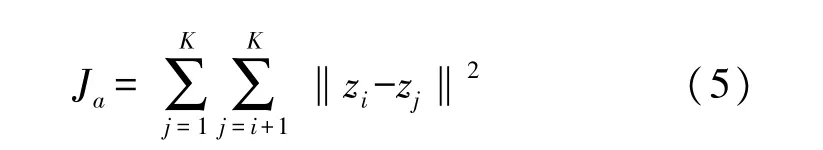
式(5)为类间距离，zi和zj分别表示第i个和第j个聚类中心点，K表示类中心点的个数，Ja的值越大越好，其值越大表示类与类之间的区分度越大，判别效果较好。

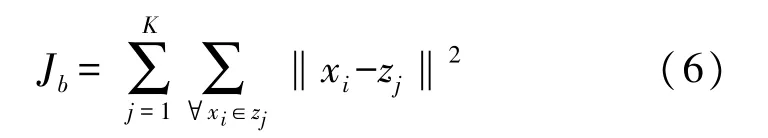
式(6)表示类内距离，zj和xi分别表示第j个聚类中心和属于此类中心的样本数据，K表示类中心点的个数，Jb的值越小越好，其值越小表示聚类中心点的选取较好，同一类分布的较为紧密。

式(4)确定的适应度函数可保证较大的类间距离和较小的类内距离，实现对电力缺陷的准确聚类，且将类间距离和类内距离做商后取对数，避免二者商值过大，造成适应度函数的过度敏感，保证聚类过程中算法的稳定性。

1.3 基于DS 证据理论的电力缺陷等级融合

由于DS 证据理论可以利用合成规则将算法多次判别结果进行决策融合[21－22]，避免算法单次判别产生的偶然性。因此为提高电力缺陷等级确定的准确性和稳定性，本文使用DS 证据理论作为MOA 算法决策融合的工具，实现电力缺陷等级的准确确定，过程详述如下。

首先，利用MOA 算法对向量化缺陷数据在最优搜索半径下的50 次运行结果，构建如式(7)所示表征缺陷等级M精确信任函数[23]的基本概率分配m函数；然后按照式(8)所示的Dempster 合成规则对上一步构建的50 组m函数进行融合，得到合成后的基本概率分配[24]；最后根据合成后的基本概率分配实现对缺陷等级的准确确定。

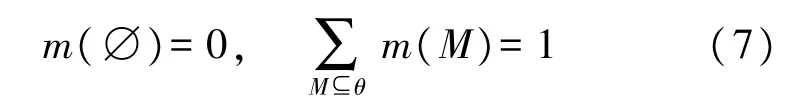
式中:θ＝{紧急，其他，一般，重大}表示缺陷等级M的识别框架，识别框架内的m函数和为

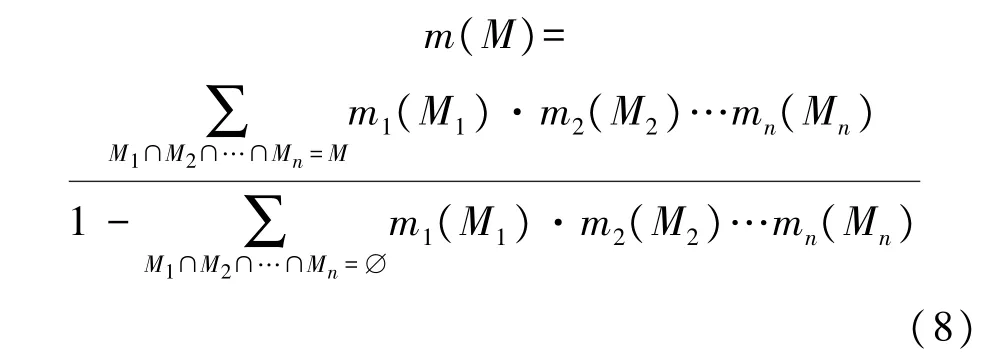
式中:m(M)表示决策融合50 次MOA 运行结果后确定的缺陷等级m函数，分子表示同一组缺陷数据50 次运行结果中被分为同一等级M的m函数乘积和，其值小于1。

2 实验过程及结果分析

以西南某地区电网公司的5 863 条变压器缺陷记录作为实验数据，其中一般、紧急、重大、其他缺陷数目分别为3 382、1 164、260、1 057 条，按照4 ∶1 的比例随机选取其中的4 743 条为训练样本，剩下的1 120 条为测试样本。

首先按照1.1.1 节的描述对变压器缺陷描述进行分词并向量化，同时根据本文1.1.2 节建立的灯色缺陷等级辨识对应权值表将实验数据中红绿灯信息向量化；最后利用MOA 算法将预处理后的训练集缺陷描述和向量化的电网红绿灯信息在不同局部搜索半径下自动等级确定，寻找判别准确率较高的最优搜索半径区间，寻找过程如下。

设定MOA 算法的最大循环次数为200，全局搜索元个数为4，局部搜索元个数为20，使用训练样本作为输入，令局部搜索半径r从0.1 逐渐递增到10，获得各自对应的等级判定准确率，如图5 所示。

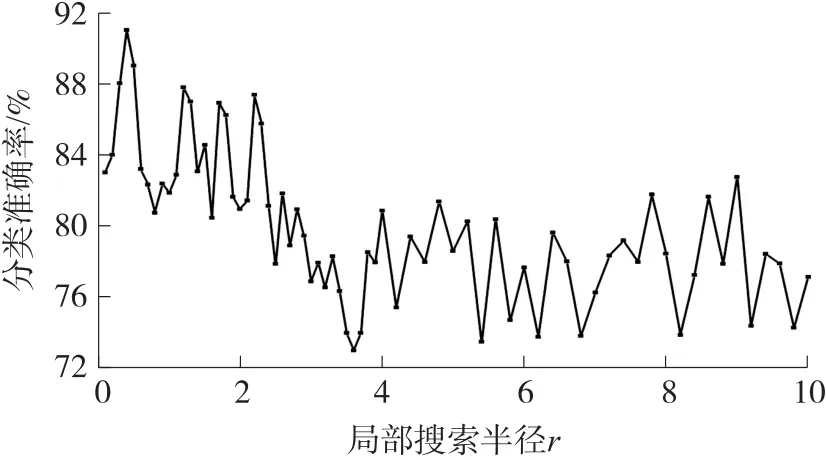
图5 训练集不同局部搜索半径r 下准确率

由图5 可见，局部搜索半径在区间[0.1，2.3]有较高的准确率，判别效果较好，随着半径的不断增大，准确率总体有所下降。这是由于固定循环次数下，随着局部搜索半径的增大，算法搜索精细度下降，使准确率降低，因此确定局部搜索半径的区间为[0.1，2.3]，并选择训练集分类准确率最高时局部搜索半径为0.4 的4 个等级聚类中心作为测试集等级的匹配中心，通过欧氏距离比较，将测试集4 个聚类中心分别归为距离最小的类别中。

为进一步提高判别准确率，使用DS 证据理论对测试集中MOA 算法50 次判别的结果进行决策融合。为详细说明决策融合的过程，从测试集一般、紧急、重大、其他四种缺陷等级中各随机选取一组数据，对表6 所示的MOA 算法在局部搜索半径区间为[0.1，2.3]，间隔为0.2 的前三次运行结果进行说明。

根据表6，DS 证据理论基本概率分配m函数按照同一次下同一组数据在不同半径下被分为不同等级的次数占12 次结果的比例进行构造，构造结果如表7 所示。例如:选取第一次实验中期望等级为一般的数据，统计发现12 次判别中有9 次被分为一般，2 次被分为紧急，1 次被分为重大，0 次被分为其他，因此m1(一般)函数在缺陷等级为一般、紧急、重大、其他的m函数分别为0.75、0.17、0.08 和0。

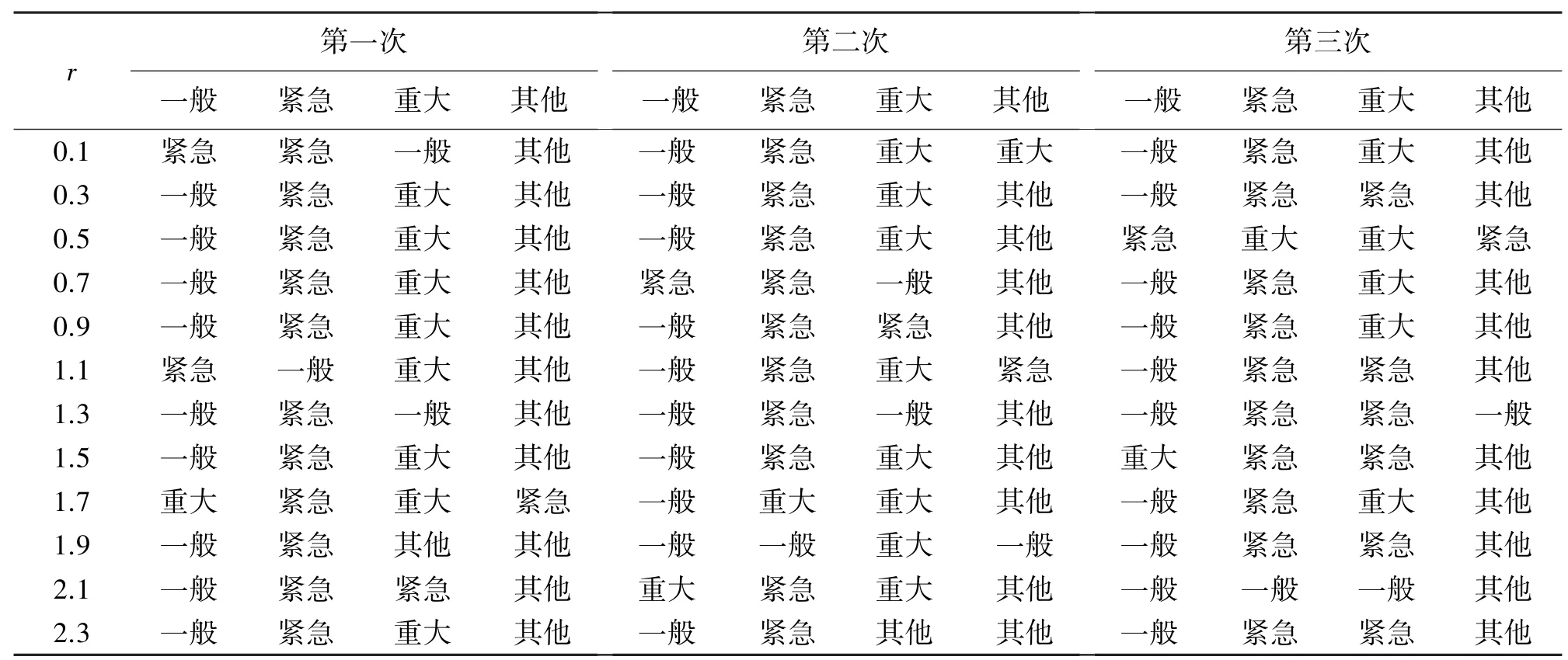
表6 4 组数据在不同半径下前三次运行结果

表7 前三次运行结果的m 函数

按照式(8)将表7 中4 组数据在12 个局部搜索半径下的前三次运行结果决策融合，融合后的m函数分配如表8 所示。

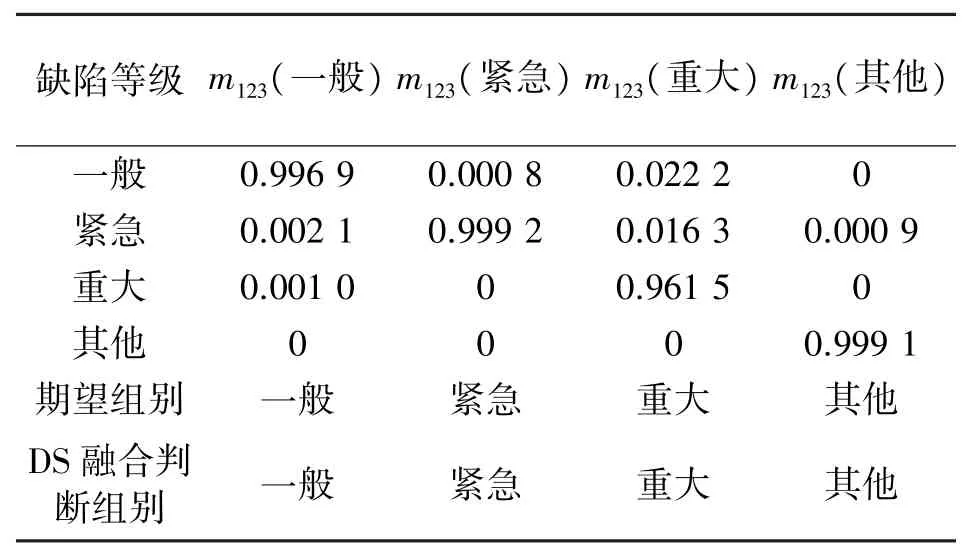
表8 DS 证据理论融合结果

对比表7 和表8 可以看出使用DS 证据理论决策融合后，表7 中第三次重大组中误分为紧急的电力缺陷正确纠正为重大。由此可见，DS 证据理论的使用避免了算法单次运行结果的偶然性对等级确定的影响，达到了提高自动判别准确率的目的。

为验证本文所提方法在电力缺陷等级确定中的有效性，将局部搜索半径区间为[0.1，2.3]，运行次数为50 次且使用DS 证据理论的MOA 算法(MOADS)与局部搜索半径为0.4，运行次数为1 次且未使用DS 证据理论的MOA 算法以及K值为4 的kmeans 算法对1120 组测试数据的聚类结果从平均准确率、平均召回率以及平均F值3 个评价指标进行对比，结果如表9 所示。

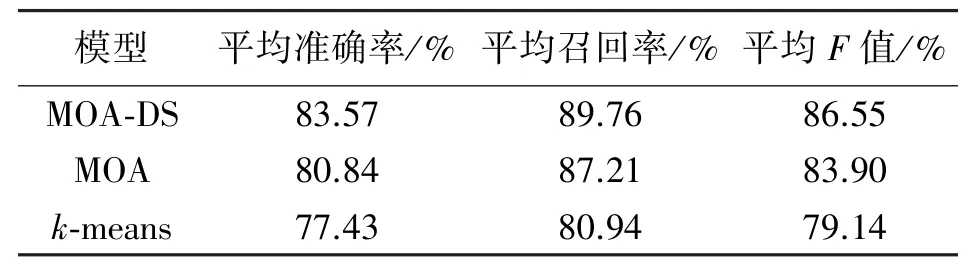
表9 三种模型下评价指标比较

表9 可以看出，使用DS 证据理论融合后的MOA 算法平均准确率可达83.57%，相比未进行DS证据理论融合的MOA 算法平均准确率提高了2.73%，相比k-means 算法平均准确率提高了6.14%，且平均召回率和平均F值均有明显提升，验证了本方法的有效性和可行性。MOA-DS 模型相比MOA 模型有较大提升的原因是使用DS 证据理论后将MOA 算法多次运行的结果进行决策融合，避免算法单次运行结果出现的偶然性，因此提高了判别的准确性；MOA-DS 模型相较于k-means 模型有较大提升的原因是MOA 算法依托局部搜索元使聚类质心的选择更加细致、合理，且适应度函数方面考虑了类间距离，提高了聚类结果不同类别的区分度，使聚类结果更加准确。

3 结束语

本文以变压器缺陷描述和电网红绿灯信息作为研究对象，提出了一种基于MOA 算法和DS 证据理论的电力缺陷等级确定方法。该方法一方面使用MOA 算法对电力缺陷等级确定，利用全局和局部搜索元使聚类中心的选择更加细致合理，进一步提高了判别的准确性，丰富了电力文本挖掘领域的方法；另一方面使用DS 证据理论将多次判别结果进行决策融合，解决了已有模型多次运行时判别结果差异的问题。此外，本文在电力设备缺陷等级确定方面进行了有益探索，避免了运维人员确定缺陷等级的人为主观性和个人认知有限带来的判断误差，提高了判别的准确性和一致性，为缺陷等级的评判提供了参考依据，为文本数据深层次利用提供了新的思路。