双向能量流动的T型三电平光伏并网逆变器研究∗

胡卫丰，周 宇，周洪益，侍红兵，李正佳

(1.国网江苏省电力有限公司盐城供电分公司，江苏 盐城 224000；2.苏州华天国科电力科技有限公司，江苏 苏州 215002)

随着社会的发展，能源的短缺，新型绿色清洁型能源成为主流能源得到了迅猛发展。清洁能源发展的同时，为了减少能源的消耗，能量双向流动的电力电子变换器成为人们研究的重点之一。因而电源应用场所都要求变换器拓扑具有能量双向流动的功能，例如蓄电池的充放电[1]、直流微电网[2]、光伏并网等[3]。T 型三电平逆变器作为能量双向流动的变换器拓扑结构之一，在光伏并网以及储能设备之间的能量转换起到了至关重要的作用。

文献[4－5]提出了一种PQ 控制方法，在逆变器进行并网时能够对逆变器的输出功率进行控制，从而控制并网电流。文献[6]提出一种两相旋转坐标系下的并网电流控制方案，但是比例积分控制器的使用使得这一方法的抗干扰能力不足。文献[7]介绍了一种基于电流正序、负序和零序分量的控制方法，涉及多个控制器，设计较为复杂。文献[8]介绍了一种重复控制用于并网电流的调节，但是这一方法的实现较为复杂。文献[9]设计了一种滞环控制，通过调节滞环的带宽来实现稳定性，但是其参数选取较难。

本文以T 型三电平逆变器为研究对象，详细介绍了空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)策略，并在此基础上设计了电压电流双闭环控制，只需要改变参考值就可以实现T 型三电平逆变器的能量双向流动。

1 拓扑及SVPWM 调制策略分析

T 型三电平逆变器的系统结构如图1 所示。从图中可以看出，每一相均由4 个带有反并联二极管的IGBT 组成，分别为Sx1、Sx2、Sx3、Sx4，x＝a，b，c。三相结构完全相同，共用中点O，经过滤波电感L并网。直流侧两个电容中点即为O。

图1 T 型三电平逆变器拓扑

SVPWM 调制策略的基本原理是通过合成的电压矢量来代替参考电压矢量，而参考电压则是旋转电压矢量，即通过这种方式得到如何用开关状态的电压矢量得到工频正弦电压，也就是最终的输出电压[10－14]。

T 型三电平逆变器的SVPWM 调制策略实现步骤可以概括为:

(1)扇区判断:区分参考电压矢量的大小扇区；

(2)矢量选择:通过最近原则，得到合成该参考电压的三个基本矢量；

(3)计算矢量作用时间:得到这三个基本矢量的作用时间；

(4)确定开关顺序:按照开关动作最少以及损耗最小的原则，确定开关动作顺序。

大扇区Ⅰ小扇区1 的基本矢量作用时间T1、T3、T2分别与大扇区Ⅱ小扇区1 的T1、T2、T3相同；大扇区Ⅱ小扇区2 的矢量作用时间T1、T3、T2分别与大扇区Ⅰ小扇区2 的矢量作用时间T1、T2、T3相同；依据前文所述，即可得出大扇区Ⅱ小扇区3～大扇区划分如图2 所示，一共分为6 个大扇区和每个大扇区内的4 个小扇区。因此无论参考电压矢量位于何处，都能由最近的三个基本矢量进行合成得到。具体扇区判断准则可参照文献[10]。

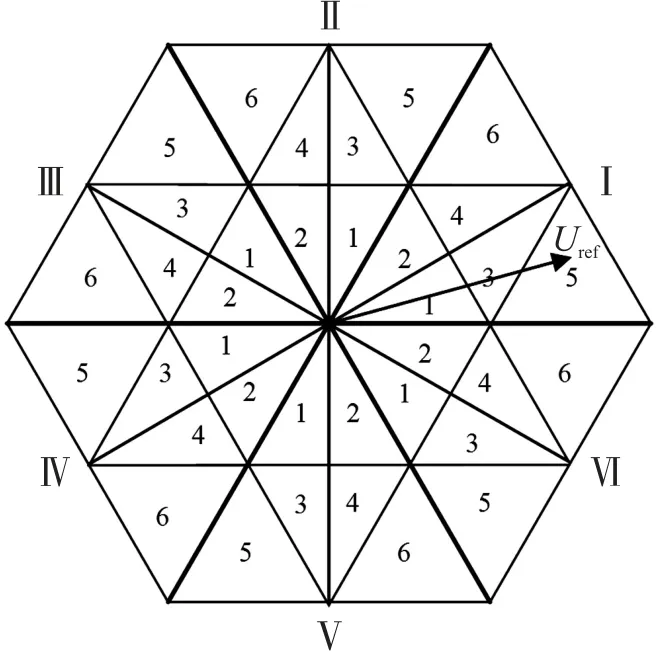
图2 扇区划分

当得到参考电压矢量所在的扇区后，即要根据最近的三个基本空间矢量合成参考电压矢量。首先要判断是由哪三个基本矢量来合成，之后根据伏秒平衡原理，即可计算出三个基本电压矢量的作用时间，如式(1)所示:

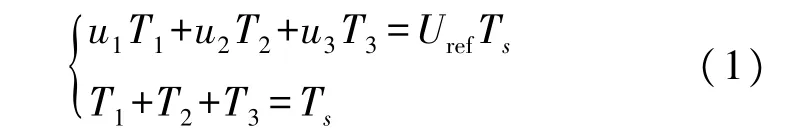
式中:T1、T2、T3为三个静态矢量u1、u2和u3的作用时间，Ts为开关周期的时间。依据式(1)即可求解得到T1、T2、T3的值，即三个基本矢量的作用时间。

如表1 所示为大扇区Ⅰ的基本矢量作用时间。扇区Ⅱ小扇区6 与大扇区Ⅰ小扇区3～大扇区Ⅰ小扇区6 矢量作用时间的对应关系。还得出得结论是奇数大扇区的基本矢量作用时间完全一致，同样偶数大扇区的基本矢量作用时间也完全一致。依据上述可得出结论，仅需要求解出大扇区Ⅰ中各小扇区所有的矢量作用时间，即根据上述结论计算得出其他所有扇区的基本矢量作用时间[11]。

表1 大扇区Ⅰ的基本矢量作用时间

得到空间电压矢量作用的时间后，选取开关状态应考虑如下三点:

(1)为了尽量减小开关损耗，在一种开关状态切换到另一种开关状态的过程中，仅能改变同一相桥臂上的开关器件状态；

(2)转换扇区时，尽量少的转换开关状态；

(3)开关状态的改变要尽量减小对中点电压波动的影响。

根据以上原则，这里采用七段式开关顺序，尽量使得开关器件状态得变换次数最少，从而减少变换器的开关损耗。

据图3 可以得出，开始为负的小矢量，且每一段仅有一个开关状态改变，七段式开关顺序以第四段呈对称关系，以此保证最优的开关顺序，同理采用该原则即可得其他扇区的开关顺序，可参考文献[11]。

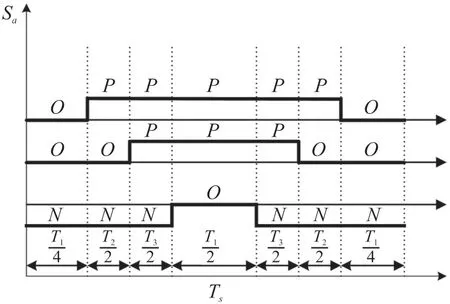
图3 七段式开关顺序图

2 电压电流双闭环控制

如图4 所示为电流解耦控制框图，在dq坐标系下，电压电流在d、q轴的分量均为直流量，且在PI 环节的调节下可以实现无静差调节，电流iq的前向通道含有关于id的负分量，而电流id的前向通道也含有关于iq的正分量，图4 为实现解耦的控制框图。

图4 电流解耦控制框图

如图5 所示为电流内环控制框图，Td为PWM信号延迟时间，一般取0.5 倍的开关周期，KPWM则表示变换器开关增益。

图5 电流内环控制框图

式(2)为电流内环的开环传递函数:

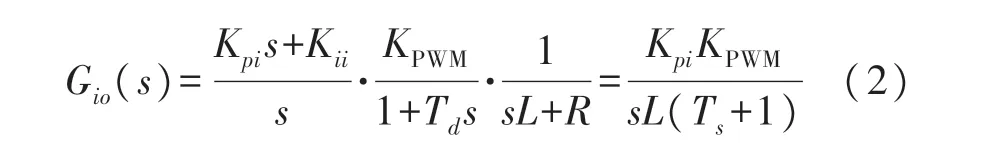
从而得到电流内环的闭环传递函数为:

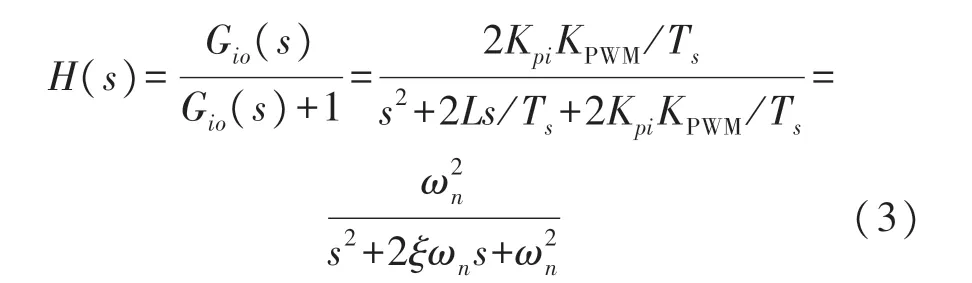
由上式可明显看出，电流内环是一个标准的二阶系统，而根据经验，一般将ξ取为0.707，系统能够具有较好的快速性、动态响应及稳定性。可取PI 参数如下:

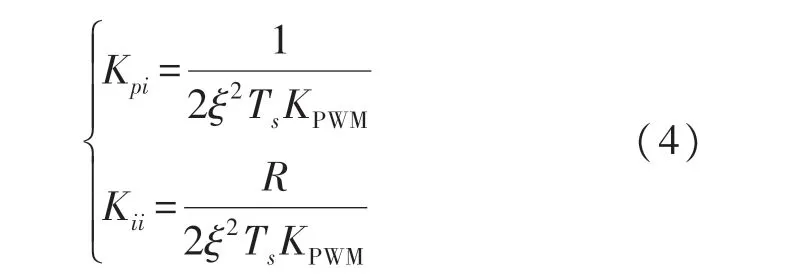
如图6 所示为电压外环控制框图，将电流内环视为惯性积分环节。

图6 电压外环控制框图

其中调制比m取为1，据此可得到电压外环的传递函数如下式:

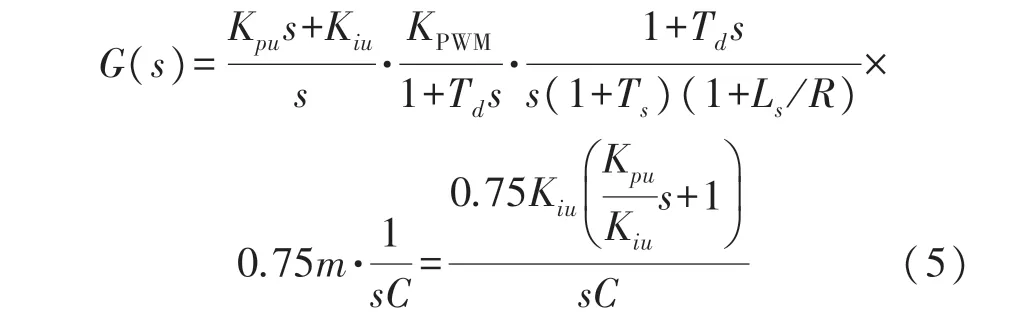
电压外环为一个二阶系统，为使系统具有较好的鲁棒性，及较快的响应速度，PI 参数可以选取为:

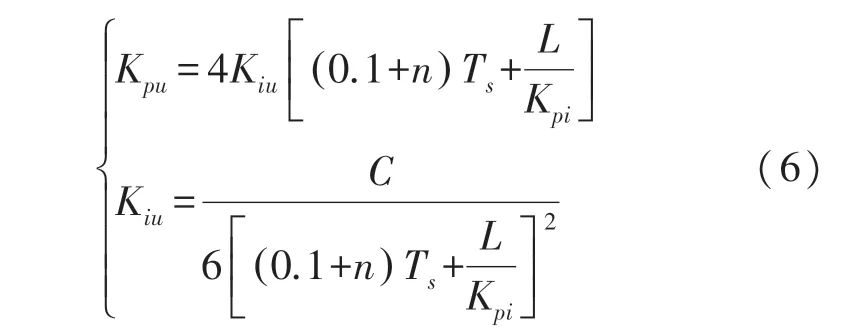
式中:n的取值范围为:0～1。

3 结果验证

为了验证本文所提的能量双向流动的方法有效性，对上述方法进行了仿真验证，同时搭建了实验平台对其进行验证。规定电流从直流侧流向交流侧为正方向。

系统仿真参数如表1 所示。

表1 系统仿真参数

(1)整流模式

如图7 所示为整流模式下的dq轴电流波形，给定id为－20 A，iq为0，以此保证功率因数，此时直流侧电压给定400 V，从图中可以看出电流跟踪效果较好。如图8 所示为并网电流和A 相电压波形，从图中可以看出，三相电流对称，同时A 相电压电流相位相反，可以证明此时工作于整流模式。

图7 整流模式下dq 轴电流波形

图8 整流模式下并网电流及电压波形

(2)逆变模式

如图9 所示为逆变模式下的dq轴电流波形，给定id为20 A，iq为0，以此保证功率因数，此时直流侧电压给定800 V，从图中可以看出电流跟踪效果较好。如图10 所示为并网电流和A 相电压波形。从图中可以看出，三相电流对称，同时A 相电压电流相位相同，可以证明此时工作于逆变模式。

图9 逆变模式下dq 轴电流波形

(3)整流模式切换为逆变模式

如图11 所示为整流模式切换为逆变模式下的dq轴电流波形，给定id为负数切换为正数，iq为0，以此保证功率因数，此时直流侧电压给定从400 V切换为800 V，从图中可以看出电流跟踪效果较好。如图12 所示为并网电流和A 相电压波形。从图中可以看出，三相电流对称，整流模式切换为逆变模式较为平稳。

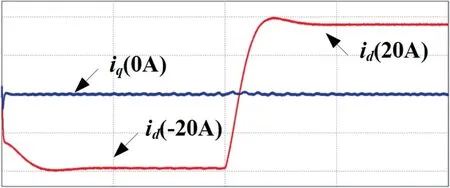
图11 整流模式切换为逆变模式下dq 轴电流波形

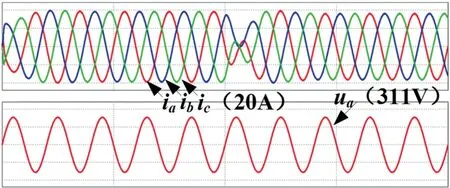
图12 整流模式切换为逆变模式下并网电流及电压波形

(4)逆变模式切换为整流模式

如图13 所示为逆变模式切换为整流模式下的dq轴电流波形，给定id为正数切换为负数，iq为0，以此保证功率因数，此时直流侧电压给定从800 V切换为400 V，从图中可以看出电流跟踪效果较好。如图14 所示为并网电流和A 相电压波形。从图中可以看出，三相电流对称，逆变模式切换为整流模式较为平稳。

图13 逆变模式切换为整流模式下dq 轴电流波形

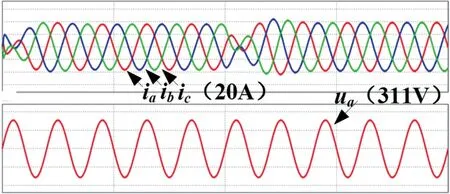
图14 逆变模式切换为整流模式下并网电流及电压波形

如图15 以及图16 所示为整流模式和逆变模式下的并网电压电流以及d轴电流波形，显然实验结果与仿真结果一致。

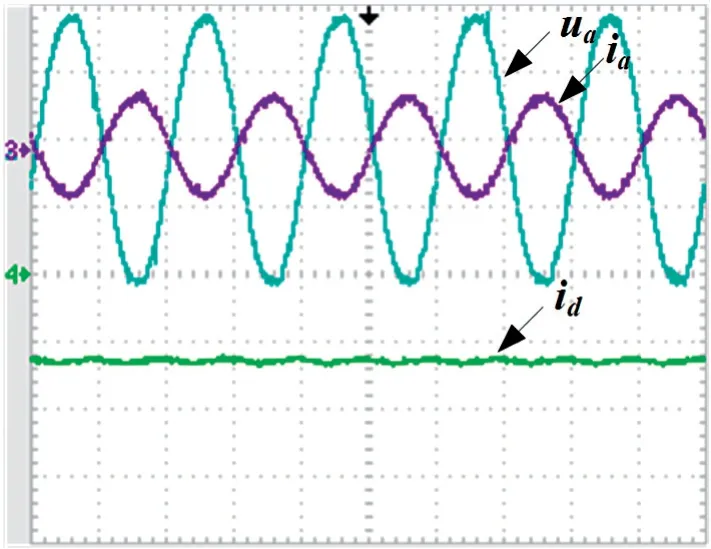
图15 整流模式下并网电流及电压波形

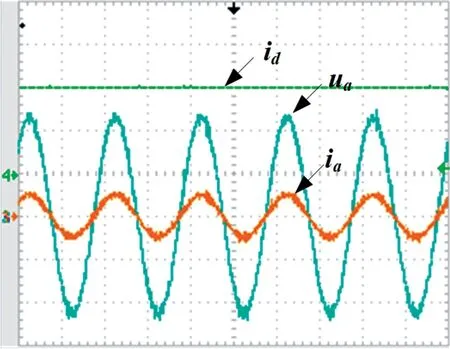
图16 逆变模式下并网电流及电压波形

4 结语

本文针对双向T 型三电平逆变器拓扑，在SVPWM 调制策略的基础上，设计了电压电流双闭环控制器，以此来实现能量的双向流动。从结果中可以看出，通过改变电流给定的正负可以控制系统工作于整流模式或者逆变模式，或者两种模式之间切换，验证了本文所提方法的有效性。