基于CLPSO模型选择的SVM电力负荷预测模型研究
夏成文,杨司玥,鲍玉昆,潘 睿,邓源彬
(1.南方电网深圳数字电网研究院有限公司,广东 深圳 518053;2.华中科技大学 管理学院,湖北 武汉 430074)
电力负荷预测主要是通过对历史上的电力负荷数据和气候等影响因素进行分析,探索电力负荷可能的变化规律,从而预先估测未来电力的需求情况[1]。负荷预测为电力系统的安全可靠供电和经济稳定运作提供了至关重要的支撑作用。随着电力系统逐步向更加智能化的方向发展,其对于高精度电力负荷预测的需求也日益提高。目前,常用的负荷预测方法大致可归纳为两类:一类是基于统计模型的传统时间序列模型,如ARIMA[2]、指数平滑法[3]及多种回归模型。此类方法要求时间序列有较好的平稳性,在非线性、非平稳的负荷预测任务中使用较为受限。另一类是以数据为驱动的机器学习技术,如应用较为广泛的神经网络[4]、支持向量机[5](support vector machine, SVM)等。此类方法对负荷序列中非结构性、非精确性的规律和模式有较好的自适应性,随着负荷及相关数据在数量和种类方面的不断丰富,机器学习方法在非线性的复杂负荷序列预测任务中也表现出了较大的潜力[6]。
尽管基于机器学习方法的负荷预测技术在精确程度方面受到了很多研究的肯定,但其预测性能往往取决于很多技术细节,比如输入特征选择和超参数优化等一系列问题,这些问题统称为“模型选择”。不恰当的模型选择会导致一些具有优秀潜力的机器学习算法在实际预测任务中的表现欠佳。解决输入特征选择、超参数优化等模型选择问题,尽可能改善模型表现,是机器学习在负荷预测领域能够发挥作用的关键。已有不少研究探索了电力负荷预测中机器学习方法的模型选择问题。其中,在超参数优化方面,张文涛等[7]采用了核极限学习机(kernel extreme learning machine, KELM)进行负荷预测建模,为了提高KELM的预测性能,引入了改进的鲸鱼算法对KELM的核函数参数和正则化系数进行优化;孙海蓉等[8]针对支持向量机在短期电力负荷预测中的超参优化问题,提出了一种二阶振荡和带斥力因子的粒子群优化算法(particle swarm optimization, PSO),改进后的算法提高了PSO对SVM各项参数的全局搜索能力,使SVM表现出更好的性能;魏腾飞等[9]将改进的PSO与遗传算法中的变异操作相结合,优化了长短期记忆(long short-term memory, LSTM)模型的多种参数,从而提高了LSTM在短期电力负荷预测任务中的准确度和稳定性。在特征选择方面,SEMERO等[10]提出了一种基于自适应模糊神经推断系统的微电网超短期负荷预测模型,采用了二进制的遗传算法进行特征选择;LIU等[11]构建了一种基于最小二乘支持向量机(least squares support vector machines, LSSVM)的短期负荷预测模型,采用小波变换与不一致率模型进行特征选择,并使用抹香鲸算法优化LSSVM的超参数。
综上可知,在负荷预测研究领域,学者对于优化算法应用于单独的特征选择或超参优化任务已有了较为充分的探索,并证实了恰当的模型选择方法对于模型预测准确度的提升有着重要作用。但在实际应用中,由于优化算法的每一轮迭代对每个解的评价都需要完成一次机器学习模型的训练,并以模型的评估函数值作为当前解的评价标准,所以利用启发式等优化算法进行一次完整的超参优化或特征选择操作,都是相对耗时的。在整个机器学习模型训练的过程中,若以嵌套的方式分别进行模型的超参优化和特征选择,耗时会大幅上升,效率较低。而在众多机器学习方法中,SVM的目标函数采用了结构风险最小化的原则,具有泛化能力好、不易过拟合、收敛速度快等优点,在负荷预测研究中应用广泛,负荷预测准确性也被反复证实[12]。同时,SVM也具有较典型的、对模型性能起到关键影响的超参数,如正则化常数C、RBF核函数的半径系数等,更适用于检验上述所提出的模型选择策略。因此,笔者采用一种基于综合型学习粒子群算法(comprehensive learning particle swarm optimization, CLPSO)的模型选择一体化策略,将特征选择与参数优化过程进行整合,进而提出了一种基于SVM预测建模方法和CLPSO模型选择一体化策略的超短期电力负荷预测方法,以提高模型的自适应能力和模型选择的效率,同时进一步提高负荷预测精确程度。
1 基于SVM和CLPSO的预测方法
1.1 基于SVM的电力负荷预测
在回归问题中,给定训练样本D={(x1,y1),(x2,y2),…,(xm,ym)},希望得到一个形如f(x)=wφ(x)+b的模型,其中φ(x)为特征空间,w为权重系数,b为偏置项。考虑到结构风险最小化的原理,设置上述问题的目标函数为:
(1)
支持向量机回归模型(support vector regression, SVR)假设可被允许的模型预测结果与真实值之间的偏差为ε,并引入了惩罚项系数(也称为正则化系数)C和松弛变量,则式(1)可转化为如下优化问题:
(2)
采用拉格朗日对偶理论进行求解,将式(2)转化为二次规划问题,可得到如下SVR形式:
(3)
式中:K(xi,x)=φ(xi)·φ(x)为核函数;xi为训练样本;x为测试数据。
在多种核函数中,RBF核函数在使用SVR进行负荷预测时较为常用,其处理非线性问题时的稳定性较强,因此笔者采用RBF核函数,其表达式为:
(4)
其中,σ为核函数的半径系数。
1.2 基于二进制CLPSO的模型选择算法设计
1.2.1 模型选择流程概述
基于二进制CLPSO算法的模型选择流程与负荷预测模型如图1所示,左侧部分为二进制CLPSO优化算法的运行流程,右侧部分为SVR模型的训练与测试过程。每个CLPSO粒子包含由一组候选输入特征和一组SVR超参数组合而成的整体编码信息;在评价粒子时,每个粒子个体在算法迭代过程中的位置取值被解码还原为对应的特征组合和超参数,用于在负荷数据的训练集上完成模型训练和模型评价,以模型的预测效果评价指标作为当前粒子的评价标准(即适应值),并据此展开下一轮的粒子更新。当CLPSO算法满足终止条件时,筛选出的最优粒子即为整个CLPSO模型选择方法所决策出的最优超参数和特征组合。最后,利用最优超参数和特征组合再次训练SVR模型,并在测试集上对模型的预测准确度进行检验。

图1 二进制CLPSO模型选择流程与负荷预测模型
1.2.2 特征与超参数的粒子表示
在CLPSO中,每个粒子包含位置和速度两个属性,其中位置属性代表问题的解,而速度属性则用于粒子的迭代更新。在本研究中,粒子的位置属性由两部分组成:特征编码和3个SVM超参数的编码。其中,特征部分是一个长度为l的0-1编码串,1表示对应位置的特征入选,0表示对应位置的特征不入选;超参数部分为3个SVM的参数C、σ、ε,分别由长度为k、m、n的0-1编码串表示。每个超参数对应的0-1编码串是一个整体,将其转化为十进制形式,即为可选超参数值序列的索引,从而与可选超参数值一一对应。一个粒子位置向量的维数为D=l+k+m+n。
特征与超参数的粒子表示示例如图2所示,假设模型的l个输入特征为从时刻t-l+1到时刻t的历史负荷值,令zi表示时刻i的负荷值;一个粒子的位置可表示为一个长度为D的0-1编码串,其中前l维对应输入特征,图2中zt-l+2和zt-1成为被选中的部分输入特征;而超参数部分,以超参数C对应的片段为例,假设参数C的可选值序列为[10-4,10-3,10-2,10-1,1,10,102,103],序列中可取值的索引分别为0~7,k=3(参数C的可选值个数为2k)。将编码“101”转换为十进制,对应值为5,表示可选值序列中索引为5的值作为参数C的取值,即这一粒子所表示的解对应参数C=10。

图2 特征与超参数的粒子表示示例
上述编码方式中,需将每个超参数的可取值个数设定为2的正整数次幂,且每个超参数的可取值按升序或降序进行排列。超参数的取值范围通常由模型的使用者依据预实验和经验进行设定,因此通过调整部分可取值以实现上述规定,理论上并无障碍,且不会对模型的最终效果产生较大影响。
1.2.3 二进制CLPSO算法
CLPSO算法是PSO算法的一种优秀变种。在传统的PSO算法中,计算并更新粒子的速度和位置时,只考虑到粒子个体自身的历史最优位置信息和整个种群的历史最优位置信息;而CLPSO算法采用综合型学习方式,即种群中其他粒子的位置信息也被纳入到更新速度的计算中。这一改进保证了种群中粒子的多样性,使得CLPSO算法的全局搜索能力比PSO算法更具优势。在CLPSO算法中,使用式(5)更新粒子的速度:
(5)
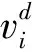
Pci=0.05+0.45×
(6)
其中,ps为种群中的个体数量。
典型粒子的索引fi(d)的确定步骤:①针对第i个粒子的每个维度,生成一个[0,1]上的随机数。如果该随机数大于Pci,则该粒子当前维度的学习对象为自己的pbest,即fi(d)=i;否则该粒子当前维度的学习对象为种群中某一其他粒子相应维度的pbest。②若确定了学习对象为其他粒子,则采用锦标赛排序选择该粒子当前维度对标的典型粒子。具体而言,随机选择两个其他粒子,比较它们的pbest适应值,选择值较小(即位置更佳)的粒子作为粒子i当前维度对标的典型粒子。③若一个粒子所有维度对标的典型粒子均为自己,则随机挑选该粒子的一个维度去对标另一任意粒子的pbest对应维度。④一个粒子的每个维度均匹配到了合适的学习对象(典型粒子)后,该粒子的所有维度就保持对标各自学习对象的pbest。⑤经历m代的更新后,重复步骤①~步骤③,重新选择该粒子每个维度对标的典型粒子。
对于二进制的CLPSO算法,粒子的速度代表了该粒子相应位置的值进行0-1变换的概率。二进制CLPSO算法的粒子更新公式为:
(7)
2 实验设计与结果分析
2.1 实验设计
实验采用了全球能源预测大赛GEFCom 2012提供的电力负荷预测比赛数据,涵盖了美国20个地理区域的小时级负荷数据,完整数据集信息及下载方式参见文献[13]。本实验随机选取了区域1和区域6的负荷数据为实验对象,针对一年当中4个典型月份(1月、4月、7月和10月)的负荷分别进行预测建模。其中,2007年4个月份的数据为测试集,每个测试月在2005、2006年对应同月的负荷数据分别作为训练集。
为了检验所提出的CLPSO模型选择一体化策略在SVR模型上的表现,在对比实验中,将所有候选特征全部输入,使用网格搜索对SVR的3个参数进行优化,3个参数的取值范围与基于CLPSO的模型一致。
2.2 输入特征与模型参数
考虑到小时级负荷的日内变化趋势和日周期性,实验选取待预测负荷的前24 h负荷序列和过去7 d(一周)内同一时间点上的负荷值,组合成为初始的候选输入特征集合。令zi表示i时刻的负荷值,则初始候选输入特征为{zt-1,zt-2,…,zt-24,zt-48,zt-72,zt-96,zt-120,zt-144,zt-72,zt-168},共30个特征。
实验中,SVR的超参数取值范围定义如下:参数C的取值范围为“以10-2为首项、102为末项、项数为32”的等比数列,对应在CLPSO的粒子中所占维数为5;参数ε的取值范围是“以10-4为首项、1为末项、项数为16”的等比数列,对应在CLPSO的粒子中所占维数为4;参数σ的取值范围为[0.05,0.10,0.20,0.40],对应在CLPSO的粒子中所占维数为2。
除了SVR模型中的待优化超参数之外,CLPSO算法中也存在部分需人为设定的参数。经过预实验的反复尝试与调整,设定种群中粒子的总数为20,终止条件为迭代次数超过200次或连续30次全局最优适应值未更新,学习因子为2,初始惯性权重为0.9,终止惯性权重为0.4,典型粒子的重置迭代次数m为8。为避免随机误差的影响,取20次实验后各评价指标的均值作为预测结果。
2.3 模型评价指标
笔者选择平均绝对百分误差(mean absolute percent error,MAPE)和均方根误差(root mean squared error,RMSE)作为评价指标。
(8)
(9)
2.4 实验结果分析
8个场景下基于CLPSO模型选择策略的SVR预测模型(CLPSO-SVR)和使用网格搜索进行参数优化的SVR预测模型(GS-SVR)的误差评价指标MAPE和RMSE结果对比如表1所示。比较两种模型的MAPE可知,CLPSO-SVR模型除了“区域6-1月”之外的其他所有场景下的MAPE均低于GS-SVR模型;而比较两种模型的RMSE可知,除“区域1-7月”外,CLPSO-SVR模型在其他7个场景下的预测表现均优于GS-SVR模型。

表1 CLPSO-SVR模型和GS-SVR模型的MAPE与RMSE对比
3 结论
笔者针对电力负荷预测中SVM等机器学习方法面临的模型选择问题,提出了一种基于综合型学习粒子群算法的模型选择一体化策略,通过对粒子的编码来整合特征选择和参数优化过程,以提高算法的自适应性和模型选择效率。实验结果证明,基于CLPSO模型选择策略的SVR在超短期电力负荷预测中的表现普遍优于使用网格搜索进行参数调优的SVR。因此,在使用SVR模型进行电力负荷预测时,相较于单独进行特征选择或参数优化过程,一体化的模型选择框架能够有效提升模型预测的精确程度,且模型的自适应性更好,所需的先验信息更少,具有较好的实际应用价值。
本研究的局限性在于:所提出的一体化模型选择框架主要适用于SVR及其他待调参数数量有限、结构较简单的浅层机器学习模型,并不能直接适用于具有深度神经网络结构的、参数更复杂多元的预测模型。随着电力负荷数据量的扩大和设备计算能力的提高,未来将考虑进一步针对一些表现突出的深度神经网络模型在电力负荷预测应用当中面临的参数优化和特征选择等模型选择问题,设计与深度网络结构更为契合、更具针对性的模型选择优化框架。

