基于偏微分去噪的结构光图像预处理方法

王麒铭

（西南交通大学，四川 成都 611756）

三维重建属于计算机视觉的重要研究内容之一。其中结构光技术使用预先定义的图像模式对待测物体进行投影，成为重构技术的一个重要分支。在结构光中，栅线投影（DFP）技术由于其空间分辨率高、测量速度快、点密度高等优点，被广泛应用于工业、医疗、娱乐等领域[1]。从变形的条纹图中提取相位是栅线投影的必要步骤。目前，傅里叶方法[2]和相移方法[3-4]是最主要的手段。但傅里叶变换精度相对较低，相移方法会引入额外的时间复杂度。因此，进行图像去噪是提升精度的直接可行方案。

与均值降噪、中值降噪等经典去噪方法相比，基于偏微分方程[5]的图像去噪更具自适应性、稳定性和精确性。二阶偏微分方程[6]和全变分（TV）模型[7]是典型的偏微分方程方法。然而，这些二阶偏微分方程往往产生一个分段恒定的图像，因此可以在其强度值平滑变化的区域中产生阶梯效应。为此基于集合测度论和原始图像的结构的MTV 方法被提出，其采用梯度最优化取得了理想的效果。

本文将利用偏微分方程方法对图像进行预处理，来得到更高精度的测量结果。

1 基本理论

1.1 栅线投影技术

栅线投影法利用投影仪和相机光轴成一定的角度来构建三角关系，通过相位和高度的映射得到被测物体的三维轮廓。在本文，将不同灰度值视为三维物体的不同高度，构建了相位与二维图像灰度值的映射关系。

设P 为投影仪光心，C 为相机光心。O 为相机光轴和投影仪光轴的交点。L1 和L2 分别为相机光心和投影仪光心到X 轴的距离，d 为相机光心到投影仪光心沿X 轴方向上的距离。设PO与AC 相交于M点，A-B-O 平面为假设的虚平面且平行于投影仪光心和相机光心的连线PC。求得高度Z 如下：

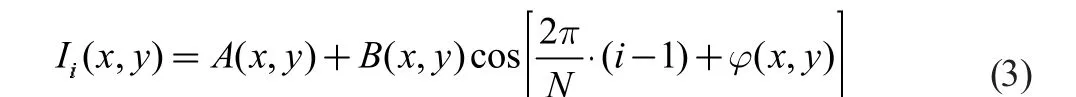
其中i=0，1，2，…，N-2，N-1。方程组共有N 个方程，三个未知量，原理上当N≥3 时即可求解。在实际操作中，为了保证求解的精度，一般取N≥4。采用Matlab 中peaks 高度分布和相位分布如图1 所示。

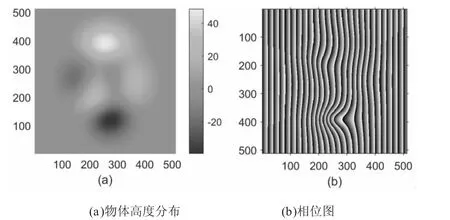
图1 高度相位关系

方程可以转化为以下形式：

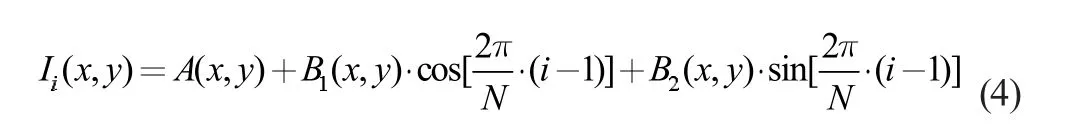
其中i=0，1，2，…，N-2，N-1。通过以下参数代换B1（x，y）=B（x，y）·cos[（φx，y）]，B2（x，y）=-B（x，y）·sin[φ（x，y）]，待求方程组表述为：

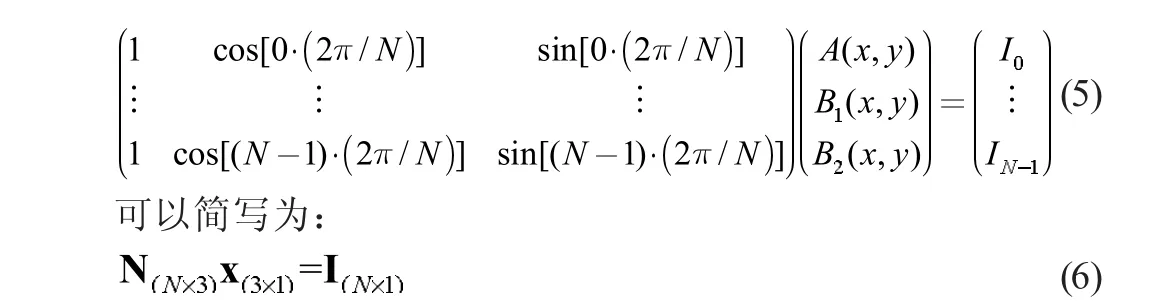
根据对B1（x，y）与B2（x，y）的构造可知tan[φ（x，y）=-B2（x，y）/B1（x，y）]，结合超定方程的最小二乘解法x=（NTN）-1NTI，求得φ（x，y）的最优解为：

1.2 MTV 偏微分滤波方法

假设噪声图像为I（x，y），待恢复图像为u（x，y）。则TV 模型对于图像的恢复流程对应以下函数的最小化过程：

2 数值模拟

在本文中，将采用MTV 方法对图3 中的四幅图像进行去噪处理，进一步利用文1.1 所述相位求解方法对相位进行计算。其单幅图像的去噪效果如图2 所示。

图2 MTV 方法预处理栅线图像单幅效果图

图3 相位求解对比

从图2 中可以看出，MTV 方法在基本不损失栅线细节（在图像弯曲处没有出现明显的过平滑效应）的情况下，有效地过滤了散布在测量图像中随机高斯噪音。其噪音图的相位求解结果与MTV 方法去噪后的相位求解结果如图3 所示。

基于图3 可以看出，其通过MTV 方法去噪，可以有效的将平均绝对值误差(MAE)从0.047rad 降低至0.0215rad。且去噪后的相位误差分布可以看出，本文方法有效地降低了误差的大小和规模。

3 结论

本文提出了一种运用偏微分方程对结构光图像进行预处理的方法。根据四步相移方法，分别求解出MTV 偏微分方程滤波方法使用前后投影图案对应的相位值。比较运用偏微分方程方法滤波前后相位的平均绝对值误差(MAE)，其由0.047 降低至0.0215。

本文方法在结构光三维重建在应用的基础上扩大了偏微分应用。另一方面，由于去噪过程没有考虑结构光自身的模态信息，对结构光信息的影响也并未考虑。在今后的工作中，还应围绕上述内容展开研究。