基于改进AdaBoost⁃C4.5算法的降雨预测

胡玉杰，杜景林，董 亚，滕 达

（南京信息工程大学，江苏 南京 210044）

降水预报是当今世界最重要和最复杂的任务之一[1]。短期高强度降水可能会引发洪水、山体滑坡、泥石流等严重性自然灾害[2]。在这种情况下，降水预报的高精度性会对社会经济生活具有重要意义。近年来，数据挖掘和人工智能被广泛应用于天气预测领域，常见的用于降水预报的方法包括KNN、决策树、神经网络等[3]。A.Haidar等提出一种新的预测方法，首次利用深度卷积神经网络（CNN）对澳大利亚东部选定位置进行月平均降水进行预报[4]。文献[5]将传统的分类回归树（CART）算法与自适应综合采样（ADASYN）算法相结合，对与降水密切相关的温度、湿度、太阳辐射、风速和蒸发等气象要素组成的气象数据进行预报建模，对万隆摄政区进行降雨预报。然而，传统的分类方法在构建降雨预测模型时都存在着泛化能力低、精度不足的问题。针对以上问题，本文提出一种改进Adaboost⁃C4.5算法。该算法集成C4.5决策树算法，得到最终的强分类器，使预测模型的泛化能力增强。在整个迭代过程中，使用PSO算法来优化Adaboost⁃C4.5弱分类器的权重以减少权重大的冗余或无用的弱分类器。使用该模型对南京市某地面观测站进行降雨预报。实验结果表明，本文建立的降水预报模型提高和完善了预报性能，具有泛化能力强、预测精度高等优点。

1 相关算法分析

1.1 C4.5决策树算法

C4.5算法最初是由Ross Quinlan开发的基于信息增益的算法[6]。与ID3算法不同的是，C4.5决策树算法能够处理连续型属性和属性值缺失的数据，使用信息增益率而不是信息增益作为属性选择的度量标准[7]。选择信息增益率最高的属性作为给定数据集的测试属性，创建一个节点并用该属性进行标记，它的每个值都会创建一个分支，并相应地对样本进行划分，最后形成初步的决策树。通过采用后剪枝的方法来降低决策树的过拟合，提高了算法模型的精度。选择C4.5决策树作为弱分类器，主要是由于C4.5决策树在计算复杂度方面比SVM和逻辑回归算法低，而分类效果也比K近邻算法好[8]。

C4.5算法的主要思想如下：

设训练数据集D有m个不同类Ci(i=1,2,…,m)，属性A有n个不同的值{a1,a2,…,an}，若使用属性A对数据集D进行划分，则会分成子集{D1,D2,…,Dn}。主要计算公式如下：

1）数据集D的期望信息为：

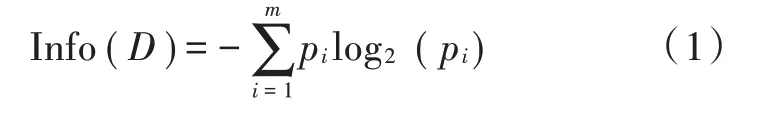
式中pi为数据集D中第i类样本所占的比例。

2）以属性A划分数据集D所需的期望信息：

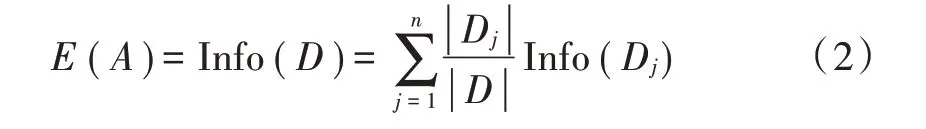
3）计算属性A的信息增益：

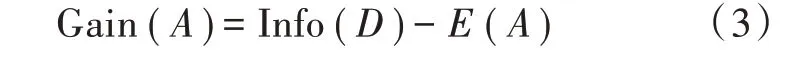
4）由于信息增益倾向于选择具有更多值的属性，为了减少信息增益带来的偏差，C4.5算法引入分裂信息作为惩罚因子，如式（4）所示，然后得到信息增益比，如式（5）所示。

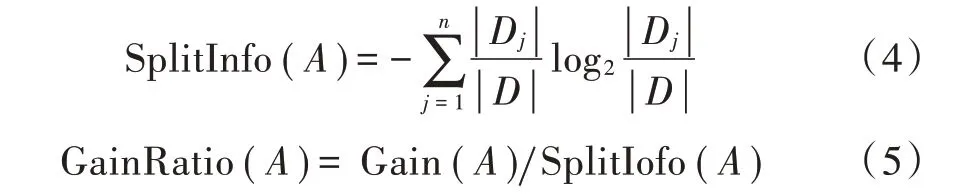
1.2 Adaboost⁃C4.5分类算法

AdaBoost是一种典型的集成算法[9]，其核心思想是通过训练多个弱分类器组合为一个强分类器来提高分类性能。在初始化时，所有的训练样本都分配了相同的权重，然后经过T轮训练后，得到T个弱分类器。每一轮训练结束后，计算弱分类器的误差率，对分类错误的样本赋予较大的权重，对分类正确的样本减少其权重。这样，在下一次迭代中，分类器将更加集中学习错误分类的样本。最后，将所有生成的弱分类器组合成强分类器。本文选取C4.5决策树算法作为弱分类器，其模型结构如图1所示。AdaBoost⁃C4.5算法的具体步骤如下：

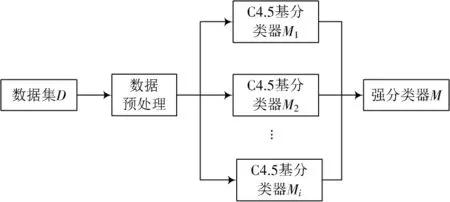
图1 Adaboost⁃C4.5模型结构

输入：训练数据集S={(x1,y1),(x2,y2),…,(xN,yN)}，其中，N表示训练样本数，xN表示样本的特征向量，y∈Y={1,0}，迭代次数T，弱分类器ct(xi)。

步骤1：初始化训练样本的权重分布，D1=

步骤2：对于t=1，2，…，T，其中，T表示迭代次数。

1）根据权重分布调用分类器ct(xi)，得到弱分类器ct：X→Y；

4）更新训练样本的权重分布，Dt+1=其中，归一化因子

1.3 粒子群算法

粒子群算法（PSO）是由James Kenney和Russ Eberhart在1995年提出的[10]。该算法来源于对鸟类捕食行为的研究，是一种基于迭代的方法，它把每个解看作是一只鸟，表示一个粒子。每个粒子都有一个自适应值，该值代表其自身解决方案的当前状态。在每次迭代中，每个粒子根据全局最优解和自身找到的最优解来调整自己的运动方向和速度，逐步逼近最优粒子。

假设有m个粒子在N维目标空间中寻找最优解，空间向量Xi=(xi1,xi2,⋅⋅⋅,xin)表示粒子群中第i个粒子的位置，向量Vi=(vi1,vi2,⋅⋅⋅,vin)表示第i个粒子的速度，其中，i=1，2，…，m，那么，粒子i当前的最佳位置Pi=(pi1,pi2,⋅⋅⋅,pin)，整个粒子群当前的最佳位置Pgbest=(pg1,pg2,⋅⋅⋅,pgn)，第i个粒子继续更新迭代得到如下：

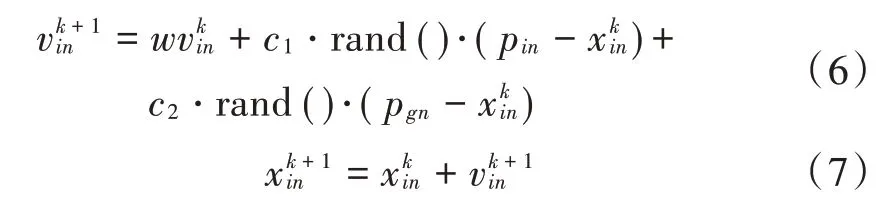
式中：w表示惯性权重；c1，c2表示加速度因子；分别表示第i个粒子在第k+1次迭代生成的速度和位置[11]。

PSO算法适用于在连续性范围内进行搜索，可以快速逼近最佳解决方案并实现参数的有效优化，易于实现，复杂度低，因此，这里可以用该算法来优化Adaboost⁃C4.5分类器的权重，提高降雨预测模型的准确性。

2 本文方法

2.1 分类评价指标

通常针对基本的二分类问题，我们考虑采用经典的混淆矩阵来表述分类器模型的性能。以降雨预报模型中有雨和无雨两类为例，该模型的混淆矩阵见表1。

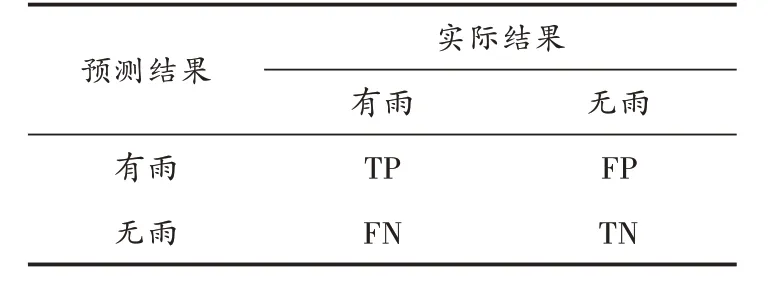
表1 模型预测与实际列联表

表1中：TP表示实际有雨预测有雨的数量；FN表示将有雨预测为无雨的数量；FP表示将无雨预测为有雨的数量；TN表示表示实际无雨预测无雨的数量。在本文的降雨预报模型中，为评价晴雨预报的性能效果，文中基于混淆矩阵，采用国内外通用的降雨预报评价指标：准确率、TS评分和漏报率（MAR）[12]，其计算公式分别为：

2.2 基于改进Adaboost⁃C4.5算法

本文利用PSO算法快速收敛、优化精度高的特性，提出一种改进的Adaboost⁃C4.5算法。主要改进在于将Adaboost⁃C4.5分类器的误差函数作为适应度函数，并用PSO算法优化Adaboost⁃C4.5弱分类器的权重，以较高的精度将较大的权重分配给弱分类器，将较小的权重分配给冗余和无用的弱分类器。当弱分类器处于局部最优时，可以重新初始化来进一步优化弱分类器的权重系数。根据改进后算法生成的弱分类器，将权重系数记为A=(a1,a2,⋅⋅⋅,an)，n表示弱分类器个数，粒子初始位置和速度分别为xi，vi，可以使用Adaboost⁃C4.5弱分类器权重系数作为粒子的位置分量，将弱分类器的错误率ei作为粒子的适应度值，粒子个体最优位置记为Pi，全局最优位置记为Pgbest。优化流程图如图2所示。

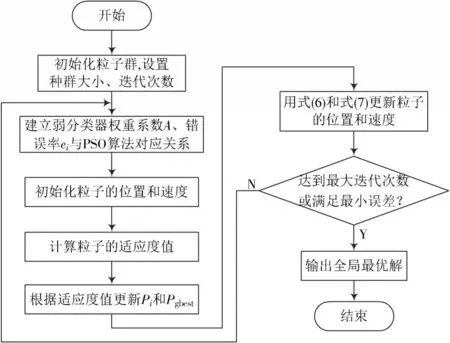
图2 PSO优化Adaboost⁃C4.5弱分类器权重流程图

传统的自适应增强算法集成弱分类器的组合模型，在迭代的过程中，通常，这样就确定了弱分类器的权重系数，而这些系数是不能改变的，因此，就不可避免地产生了一些冗余和无用且权值较大的弱分类器，这极大地影响了分类器的性能。因此，在采用集成学习方法对多维数据集进行分类预测时，应当充分考虑到弱分类器的权重分配问题。基于以上的改进，把这种算法应用于降水预测中，其改进算法执行过程如图3所示。

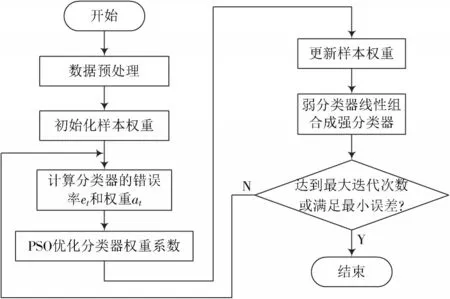
图3 改进Adaboost⁃C4.5算法执行流程图

3 实验与分析

3.1 数据选取及处理

本文实验数据选取南京市2016—2019年的6—8月某点观测站的气象数据资料，任何一条数据的气象要素包括大气压强（单位：hPa）、气温（单位：℃）、风向（单位：（°））、风速（单位：m/s）、相对湿度（单位：%）、每小时降雨量（单位：mm）。其中，把前5个气象要素作为降雨分类预测的输入属性，把是否降雨作为输出属性，数据来源于中国气象数据网。部分原始气象数据如表2所示。

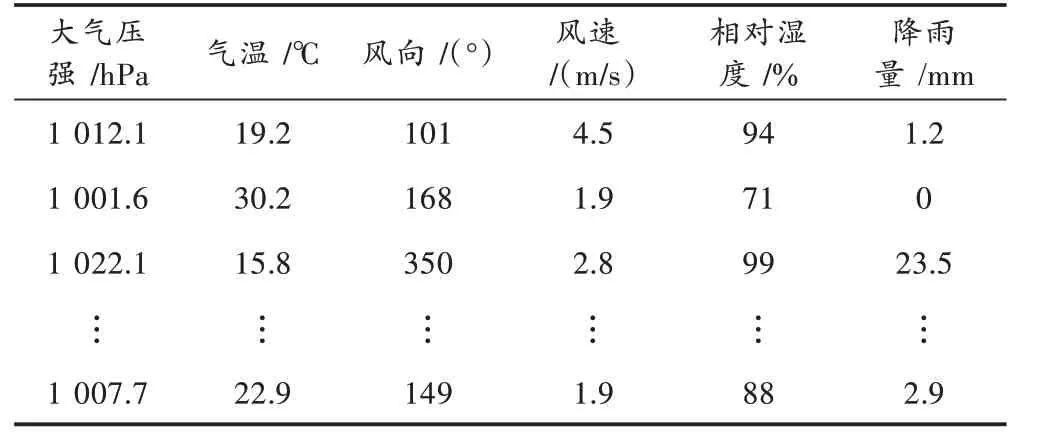
表2 部分原始气象数据

在获取数据后，属性可能会有缺失值，为处理这个问题，可以使用属性的平均值来填补缺失值，以获得更好的准确性。由于不同的气象要素通常具有不同的量纲和数量级大小，为了让气象要素之间具有相同的量纲和数量级而能够相互产生可比性，需要对样本数据进行归一化处理，通过函数变换将样本数据的各要素值映射在[0,1]之间，具体归一化公式[13]如下：

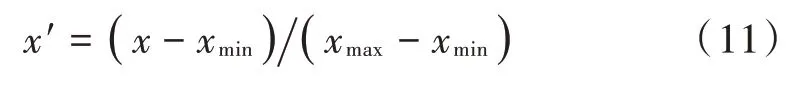
式中：x代表样本属性值；xmax和xmin分别代表样本数据中各气象要素值的最大值和最小值。

3.2 降水等级模型建立

本文研究了对降水等级的预测，将上面提出的5个气象要素作为输入，对降水等级进行分析，按照国家防汛部门对1 h降雨量等级的划分，建立5个等级预报降雨模型，具体降雨等级划分见表3。

表3 1 h降雨量等级划分

3.3 实验结果与分析

为了验证本文的改进后算法在降水预报模型上的先进性，在此将本文方法与其他两种降水预报模型作对比，分别进行了降水量等级预报和晴雨预报，其他两种降水模型分别是基于C4.5决策树算法的降水预报模型和基于Adaboost⁃C4.5算法的降水预报模型。在实验中采用10⁃折交叉验证方法将数据集随机分为10份，其中，9份作为训练，1份作为测试，将10次实验的结果平均值作为最终的评价标准。在实验之前，设定实验基本参数，粒子群规模N=50，学习因子c1=c2=1.494，惯性权重系数w=0.729，最大迭代次数Tmax=50。

首先，选择利用PSO改进后Adaboost⁃C4.5算法和传统Adaboost集成C4.5算法在构建不同弱分类器个数的情况下，比较两者对样本的分类精度，如图4所示。

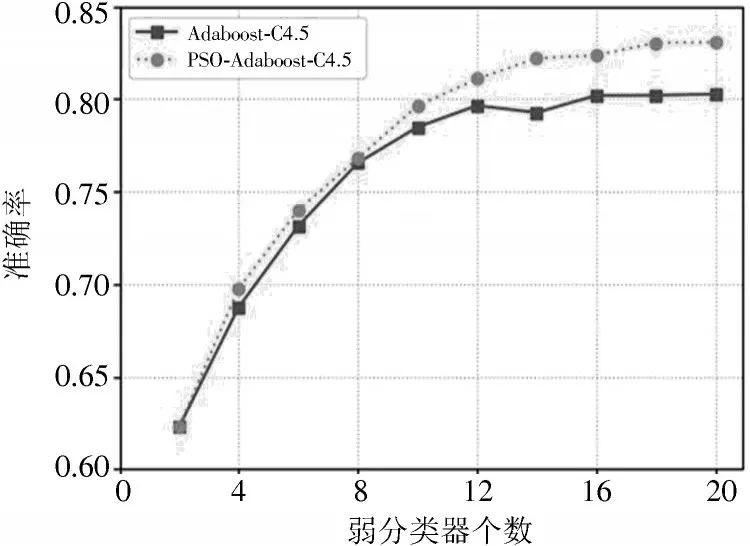
图4 两种强分类器准确率对比

由图4可以看出，随着两者构建弱分类器个数的增加，线性组合的强分类器对样本分类的准确率也在增加。随后，慢慢趋于稳定，改进后的Adaboost⁃C4.5算法在弱分类器个数达到18~20时趋于稳定，而前者在弱分类器个数达到16时便出现饱和，在T=18时，改进后的Adaboost⁃C4.5算法比传统Adaboost⁃C4.5算法的准确率高了2.8%。在1 h降雨量等级预报实验中，固定迭代次数T=18，计算三种模型的降水预报标准误差见表4。由表4中可以看出，由于各类样本所占的比重不同，三种分类器对不同降水等级的预报效果也不同。三种算法对0级和1级降水表现出很好的性能，对降雨量大的样本表现出较差的性能，但改进后的算法对3级和4级降水表现出比其他两种模型更好的性能。

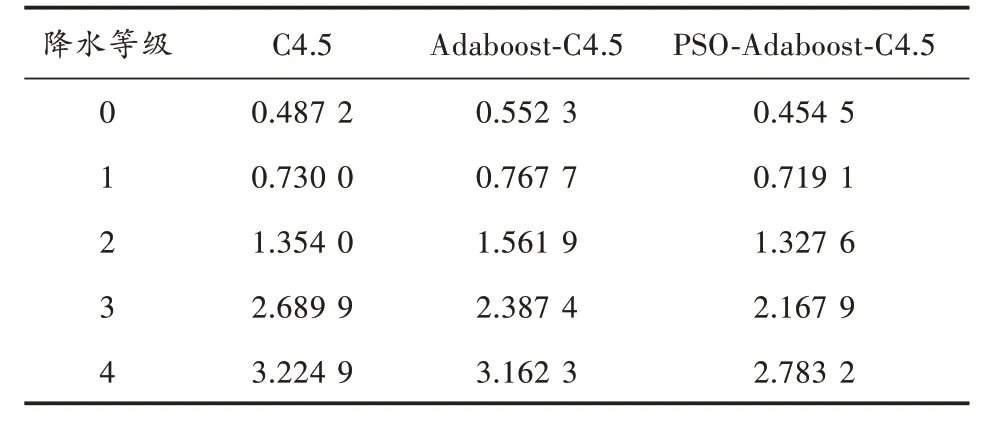
表4 三种模型的降水预报标准误差

为了进一步检验本文提出的降水预报模型性能，本文利用三种降水预报模型分别进行了晴雨预报。实验样本数分别为200，400，600，800，1 000，1 200，1 400，1 600，1 800和2 000。固定迭代次数T，晴雨预报的准确率、TS评分、漏报率如图5~图7所示。图5~图7分别显示了在不同样本数下三种降水预报模型的准确率、TS评分和漏报率的变化曲线。其中，在晴雨预报中，准确率、TS评分越高，漏报率越低，所反应的降水模型性能越好。由图5可以看出，随着样本数的增加，改进后的Adaboost⁃C4.5分类器的准确率逐渐稳定在86.5%左右，而传统Adaboost⁃C4.5分类器在样本数达到1 200以后出现了性能退化的现象，总的来说，随着样本数的增加，改进后的Adaboost⁃C4.5分类器模型在准确率和TS评分上总是高于其他两种分类器模型。由图7可以看出，改进后的Adaboost⁃C4.5分类器的漏报率在总体上低于其他两种分类器模型。当样本数达到1 400时，传统的基于C4.5算法降水模型的漏报率为35.32%，改进后的Adaboost⁃C4.5算法模型漏报率仅为25.33%，比前者降低了10.01%。

图5 三种预报方法的准确率对比

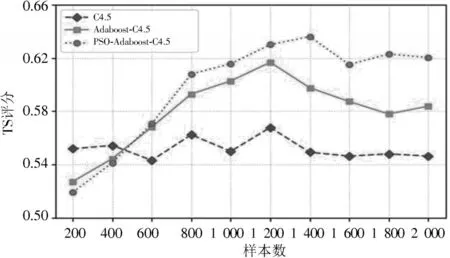
图6 三种预报方法的TS评分对比

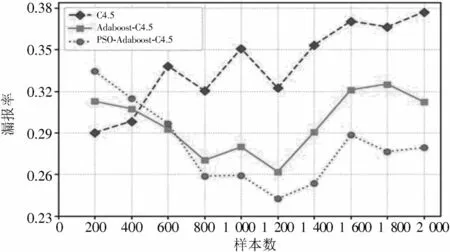
图7 三种预报方法的漏报率对比

4 结 语

本文提出了一种改进的Adaboost⁃C4.5算法，利用PSO算法来优化Adaboost⁃C4.5弱分类器的权重，可以有效地减少权重大的冗余或无用的弱分类器，从而提高强分类器的预测精度。在这个基础上，应用改进的算法构建降水预报模型。实验结果表明，本文提出的降水预报方法在总体上提高了准确率、TS评分和降低了漏报率，预报效果优于其他两种预报方法，一定程度上克服了传统降水预测模型泛化能力低、精度不足的问题，具有一定的实际应用价值。