基于公交IC卡和AVL数据的公交客流OD推算

张文胜 卢 梦 朱冀军 闫 涛 段钊宁

1(石家庄铁道大学交通运输学院 河北 石家庄 050043) 2(河北省交通规划设计院 河北 石家庄 050011) 3(交通运输行业公路建设与养护技术材料及装备研发中心 河北 石家庄 050011) 4(上海市政工程设计研究总院(集团)有限公司 上海 200002)

0 引 言

公交大数据作为交通大数据的重要组成部分之一，具有多元化、结构化的特点，蕴含了丰富的交通流特征，完整的公交客流起止站点(Origin-Destination，OD)数据是交通流特征分析的数据基础。大部分城市在公交运营系统中均采用上车一票制，乘客通过上车刷IC卡而下车不再刷卡的方式完成公交乘坐流程[1]，因此在公交原始数据中存在上车站点未记录、下车站点未知的问题。公交客流OD推算方法的研究具有重要的科研价值与社会意义。

近年来，众多学者在乘客下车站点推算方面进行了大量的研究。Farzin[2]基于出行链方法，通过公交车辆GPS数据与乘客IC卡刷卡数据的关联匹配实现了客流OD推导。文献[3-4]综合考虑了影响乘客公交出行的其他因素如时间、客流量等，分别提出了不同的公交客流OD推算方法。文献[5-8]基于出行链的思想进行了延伸与改进，利用公交线路运营数据、GPS自动定位数据等信息，实现了乘客下车站点的推导。费晔[9]基于交通IC卡在POS机上的刷卡交易数据与公交GPS车载数据，分析得出公交出行OD分布。徐文远等[10]基于公交站点客流量服从泊松分布的特点，通过参数标定建立了下车站点概率矩阵，实现了下车站点的推算。柳伍生等[11]基于区间不确定理论提出了客流OD推算方法，结合乘客多日出行特征和下车站点概率，通过区间数值处理方法得到了下车站点客流区间值。

现有方法分别从公交站点下车概率、多日出行模式、区间不确定性理论等多个方面分析了乘客下车站点的可能性，但在时间与空间综合作用下乘客下车站点推算方法的研究较少。本文从乘客出行时空特性出发，分析了乘客在不同出行距离、不同出行时间下的出行特征，研究了公交站点吸引强度的变化特点，提出公交站点吸引强度与公交出行链结合的乘客下车站点推算方法。

1 上车站点识别

公交站点数据、IC刷卡数据和车辆自动定位(Automatic Vehicle Location，AVL)系统数据是城市公交客流OD推算的数据基础，公交站点数据包含公交站点的地理位置与站点的归属信息，IC刷卡数据是乘客公共出行的实际体现，AVL数据是公交自动定位系统传回服务器的数据，包含公交车的进站、出站时间和站点信息。

在公交停靠站点时，AVL设备把公交停靠数据传输至服务器往往需要消耗一定的时间。同时，在公交离站后，不可避免会发生站后刷卡的情况。因此，针对站前站后刷卡的情况，设立弹性时间因子Δt以实现乘客上车过程的准确描述。将公交进站时间设为t进，公交出站时间设为t出，乘客刷卡时间为ti，乘客上车情况描述如图1所示。

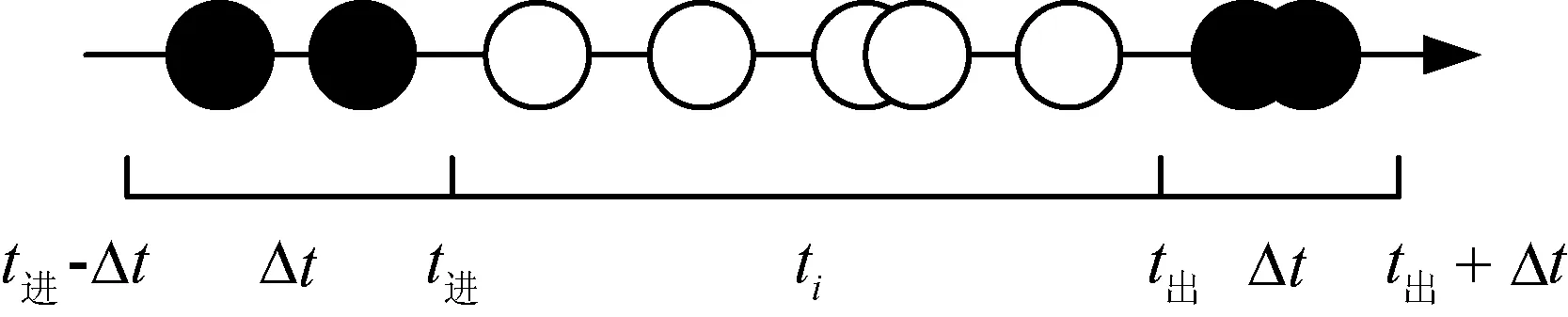
图1 乘客上车情况描述

弹性时间因子Δt的影响因素包含公交站间距、公交运行速度，在不同出行日期，公交站间距是一定的，但公交运行速度是变化的，因此选取公交线路相邻站间距与每日的线路平均运行速度比值确定Δt，Δt的修正系数设定为1/2，实现延迟数据的全时间区间覆盖，由于始发站与终点站只涉及一个相邻站点，所以不需要设定修正系数。计算如下：

(1)

式中：N为公交线路的公交站点;总数dj,j+1为公交第j至j+1站点的距离;dk,k+1为公交第k站点至k+1站的距离;Th,h+1为公交第h站点至h+1站的运行时间;Δt前为前区间弹性因子;Δt后为后区间弹性因子。

对公交到发站时间进行弹性改进后，时间匹配过程如下：

t进-Δt前≤ti≤t出+Δt后

(2)

乘客上车识别体现为IC刷卡数据与AVL数据的融合过程，两者的融合以公交站点数据为基础。通过提取IC刷卡数据、AVL数据的线路关联信息，基于线路数据与站点数据，循环匹配IC刷卡时间与公交车进站、出站时间，实现乘客上车站点的识别。上车站点识别流程如图2所示。

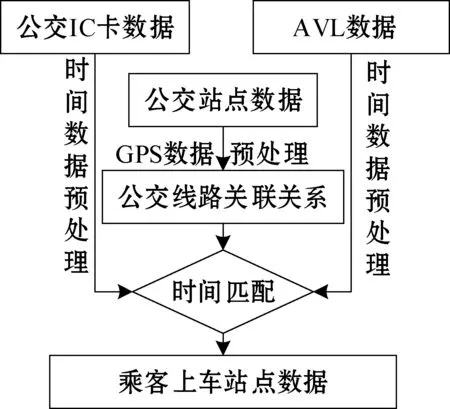
图2 上车站点识别流程

2 下车站点推算

2.1 乘客公交出行分析

乘客出行链是乘客单日从出行行为发生至结束的所有出行行为按照时间排序所形成的一个链状结构，由于出行方式的多样性，部分乘客出行链中往往存在公交车以外的出行方式。以出行链中出行方式的单一性、出行链的闭合性为主要因素进行乘客出行链分析，将乘客出行行为分为以下四种情况，如图3所示，其中：(a)为乘客单日出行只存在单次公交出行；(b)为乘客单日出行不存在除公交外的其他出行方式，且往返构成环形出行链；(c)为乘客单日出行存在除公交外的其他出行方式，但构成环形出行链；(d)为乘客单日出行存在除公交外的其他出行方式，且不构成环形出行链。

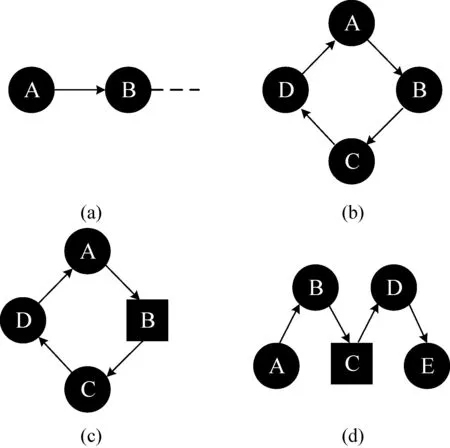
图3 乘客出行分析

闭合的乘客出行链如图3(b)、(c)所示，虽然两种出行模式的发生过程不尽相同，但是乘客最终回归到原始的出发站点，形成了环状的闭合出行链，满足应用乘客出行链方法求解的要求。开放的乘客出行链如图3(a)、(d)所示，两种情况分别表达了乘客单次公交出行与多次公交出行，基于乘客个体多日出行特征，可分别通过提取高频出行站点、公交站点吸引强度等参数推算乘客下车站点。

2.2 下车站点推算模型

当乘客出行链为环形闭合链时，利用公交出行链法推算下车站点效率与准确性较高，而当乘客单日出行只存在单次公交出行情况时，利用乘客出行链法无法进行逻辑计算。并且在乘客单日多次出行的情况中，往往存在非公交出行与公交出行相交叉的形式，乘客出行链的表现形式是非固定的，因此提出公交站点吸引强度与公交出行链结合的方式推算乘客下车站点。

在出行线路l中乘客m在i站点上车，基于公交线路上下行参数和乘客上车站点数据，将乘客在公交线路中的下游站点集合定义为Km。集合Km表达为乘客m具有下车可能性的站点集合，统计乘客m的多日出行数据，定义乘客m的高频出行站点集合Q。

针对闭环出行链，判断是否满足采用乘客出行链方法的条件。定义乘客单日公交出行次数为c，若c>1，定义匹配项公交出行线路编号为ln，当次出行线路l与ln相同时即l=ln，匹配项乘客站点j站点包含于线路l的下游站点集合K，则认为该乘客在线路l上从i站点至j站点完成了公交出行行为，j站点即为该乘客当次出行的下车站点。

(3)

式中：Pmlij1为乘客m在l线路从i站点上车至j站点下车的概率;j为匹配项上车站点;Km为乘客m在l线路中的下游站点集合;c为乘客m单日公交出行次数。

若乘客m出行次数满足c>1，当次出行线路编号l与匹配项出行线路编号ln不同时即l≠ln，若下游站点集合K中存在站点j与匹配项公交出行的上车站点之间的距离d小于公交线路平均站间距D，则j站点即为该乘客当次出行的下车站点。

(4)

若乘客出行链法无法推算下车站点，由于公交出行具有往返性的特点，高频站点集合可以同时表达乘客在公交站点上下车的频率。假设当乘客m在线路li中的下游站点中存在高频站点时，分别计算各站点高频比重集合W，选择W中的最大值ωj作为乘客下车站点概率，计算如下：

ωj=max{ω1,ω2,…,ωn}ωj∈W

(5)

(6)

式中：Pmlij3为乘客m在l线路上从i站点上车至j站点下车的概率；ωj为高频比重集合W中的最大值。

若乘客m在线路li的下游站点中不存在高频站点，采用以公交站点吸引强度为主导因子进行下车站点推算，从时空角度考虑，乘客出行距离与乘客出行时间是影响公交站点吸引强度的关键因素。由于公交线路的固定性，乘客出行距离可以通过站点分布距离直接得以体现。基于乘客的个体出行特征，乘客出行站数服从泊松分布[12]。

(7)

式中：P(k)、Pmlij4为乘客从i站上车至j下车的过程中乘坐k站的概率；k为乘客完成单次公交出行行为所经过的站点个数；λ为乘客平均出行区间站点数。

目前，公交出行链法在现有公交客流OD推算研究中，已得到了广泛的应用，基于公交出行链法推算得到的公交OD数据准确率可达90%[13]，因此基于公交出行链法计算平均公交区间站点数λ。

乘客出行区间站点数λ是公交线路、出行时间等多个因素共同作用的结果。本文选取了石家庄市区内较有代表性的东西向公交线路6路、南北向公交线路5路、跨越市区的公交线路13路和23路共四条公交线路分别计算λ值，提取了石家庄市2017年9月4日至9月8日的公交出行数据，各线路λ值分布如图4所示，各线路λ值不同，表现出在多条线路中乘客出行距离的差异性，因此，不同公交线路的λ值需要分别求取。

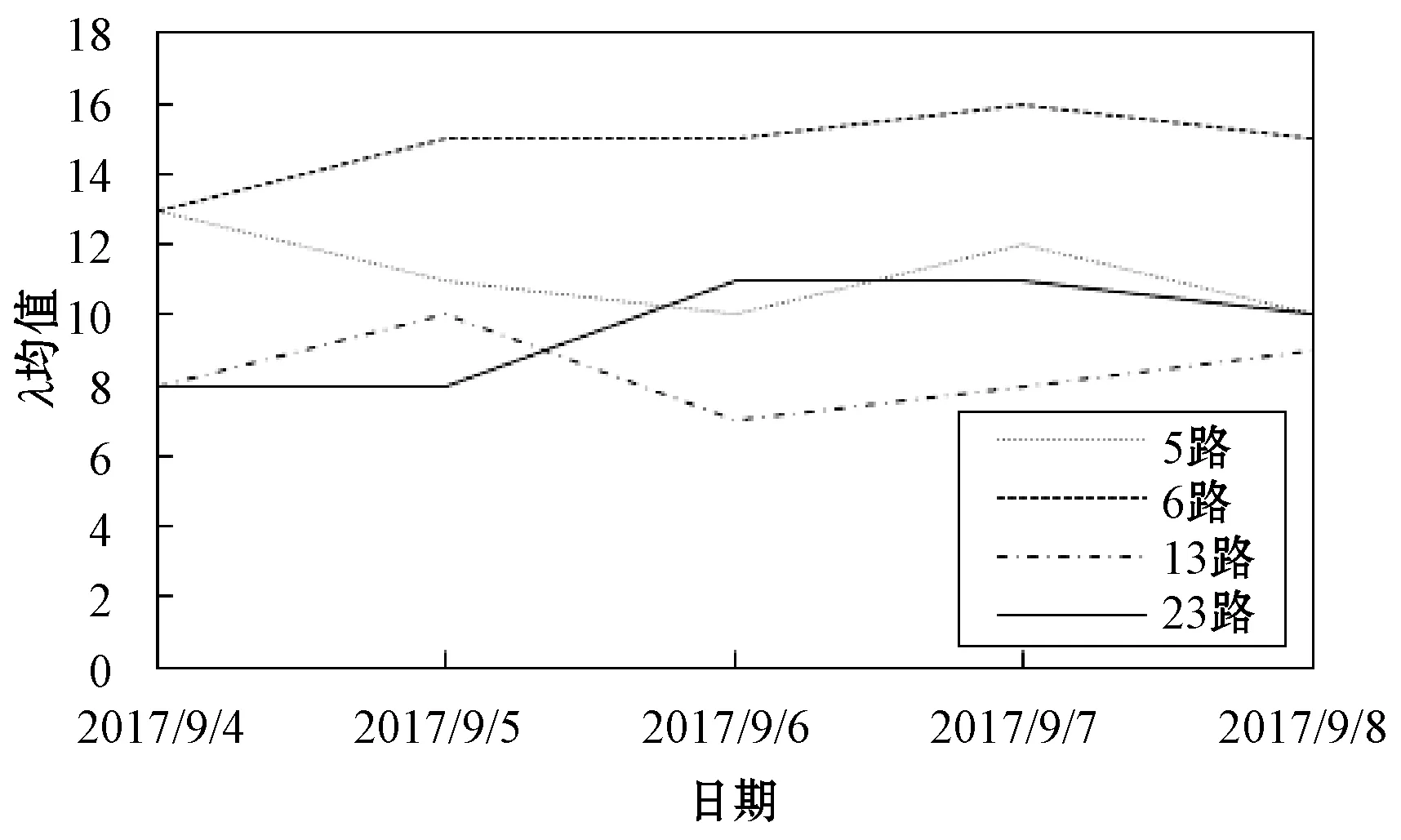
图4 多日期多线路λ值分布

针对不同的乘客出行时间，本文选取了有代表性的从二环外至市区中心跨越多个商业圈及居民区的23路公交数据，将乘客出行时间分为工作日与非工作日两种情况进行分析。选择连续四周共20个工作日的客流数据，经过统计分析，线路客流量的时间变化区间表现为早高峰、晚高峰、正常时间段，客流分布如图5所示，根据客流波峰数据，将乘客的出行时间分为7点至9点、17点至19点及其他时间共3个时间段分别计算λ值。

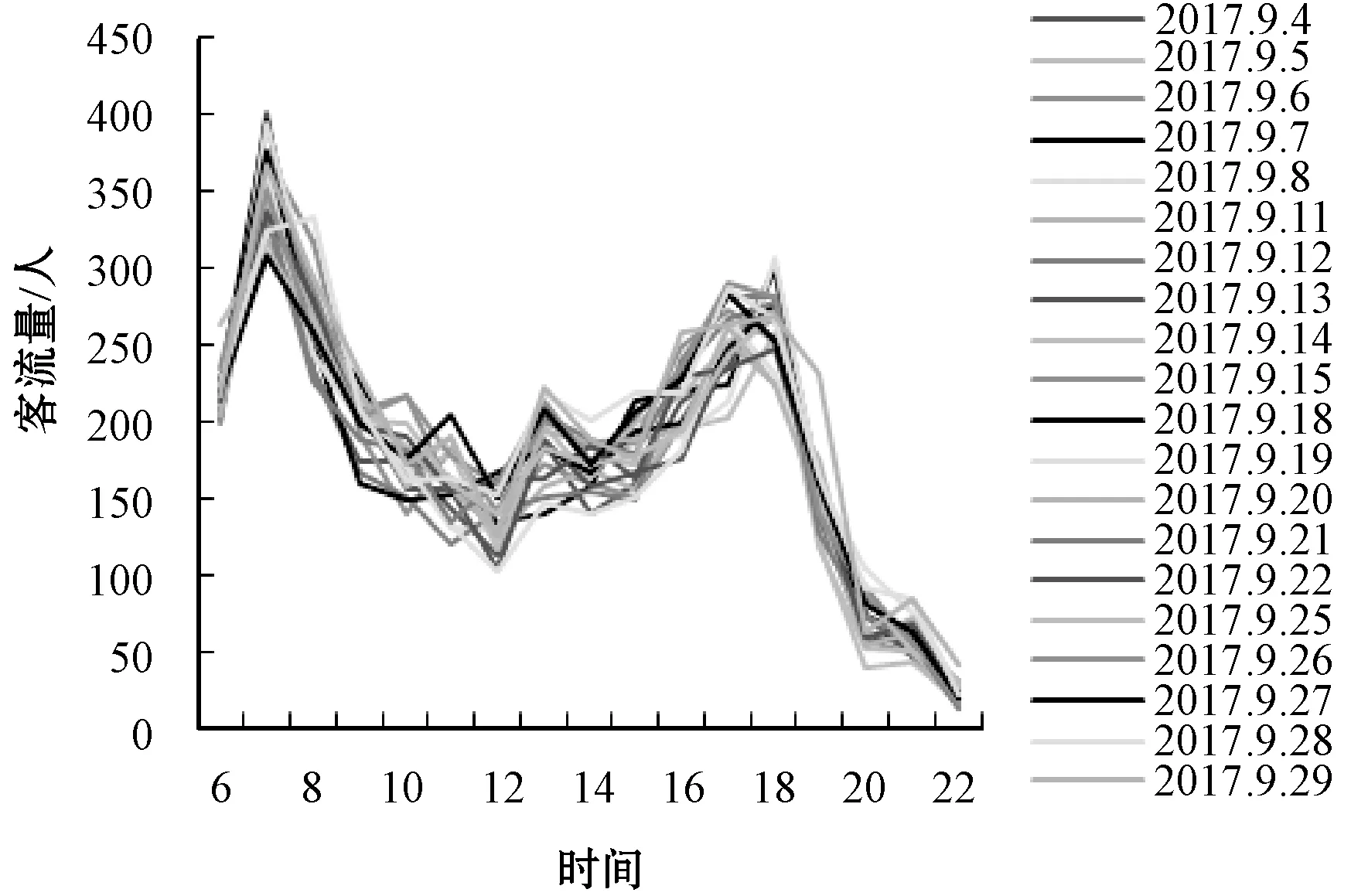
图5 工作日客流量分布

针对基于公交出行链法推算得到的23路乘客公交出行数据，分别对三个时间段进行λ值计算，得到早高峰均值λ为15.2、晚高峰均值λ为14.35、正常时间段均值λ为14.15，可知晚高峰、正常时间段的λ均值均在14左右，而早高峰的λ均值在15左右，反映出城市居民早高峰出行距离比晚高峰、正常时间段要长。在计算公交站点吸引强度时，需要根据出行时间分别计算公交站点吸引强度，因此早高峰λ取值为15，晚高峰和正常时间段λ取值为14，从而体现乘客出行距离随时间变化的特征。

针对非工作日出行行为，选择了连续四周共8天的客流数据进行分析，线路客流量如图6所示。非工作日的客流量分布曲线较为平缓，在大部分时间内客流量波动不大，表现出非工日下乘客出行距离不再受时间影响，因此不再对非工作日分时间段，计算得均值λ为15。

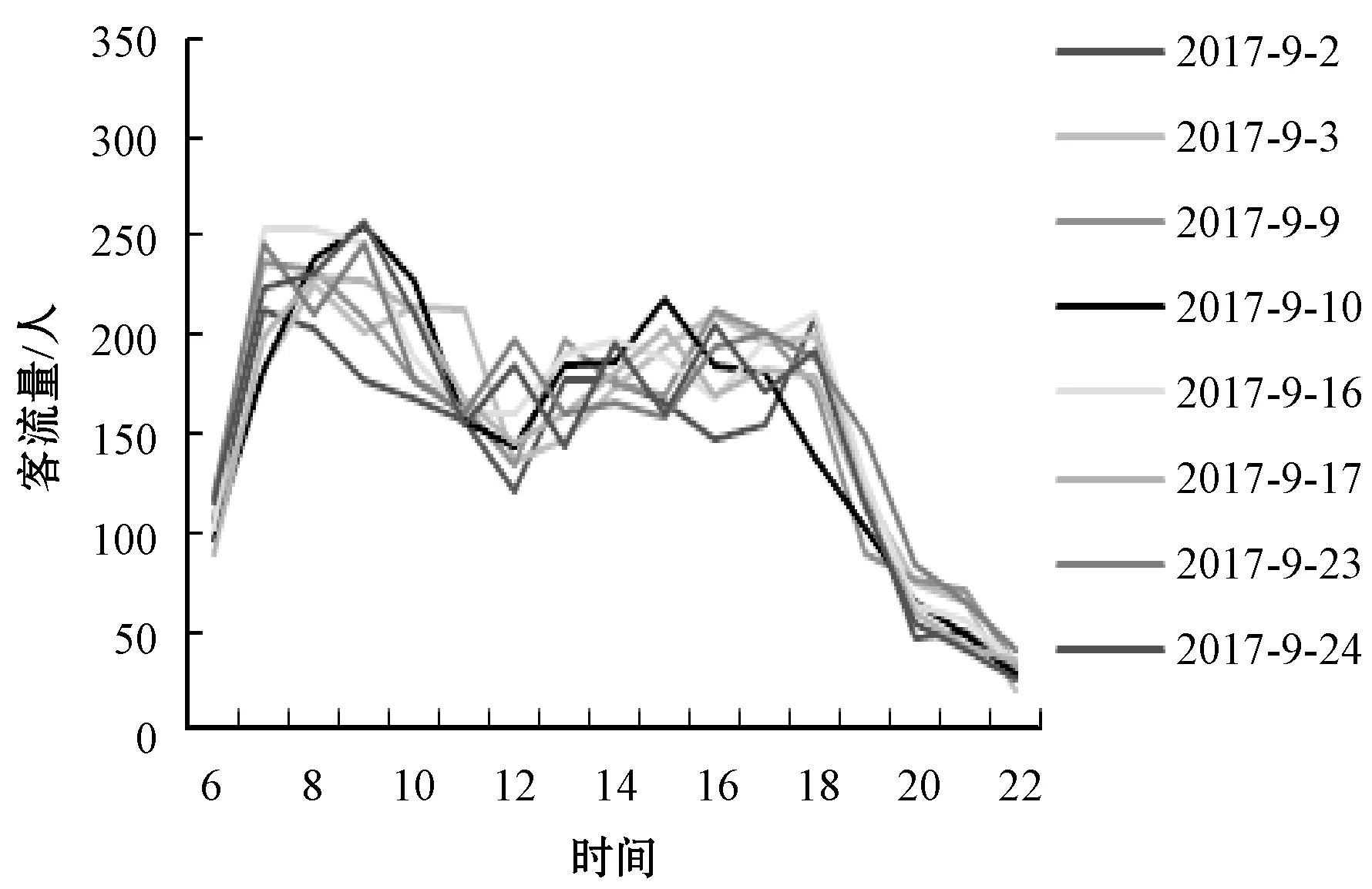
图6 非工作日客流量分布

2.3 模型有效性检验方法

基于公交出行链思想，假设城市居民均采用公交出行的方式，各个站点的公交出行产生量与吸引量应基本相等。由于公交客流OD推算的目的是为公交群体客流特征研究提供数据基础，单个乘客的精确度并不影响集计层面的断面客流、满载率和方向不均匀系数等指标，因此在集计层面上通过公交出行产生量与吸引量检验公交客流OD推算模型。

采用回归分析的方法进行模型有效性检验：

Y=b+a·X

(8)

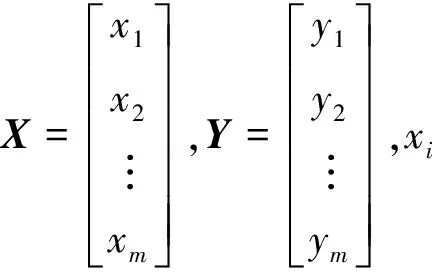
采用最小二乘法对回归系数进行估计：

(9)

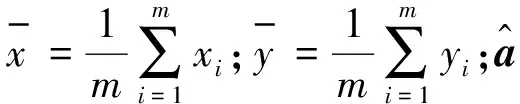
采用R2检验方法检验回归系数的拟合程度：

(10)

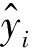
3 城市公交客流OD识别的验证与应用

3.1 乘客上车站点识别

以2017年9月4日23路公交数据为例，当未设置弹性时间因子Δt时，匹配得到乘客上车站点信息340 020条，匹配成功率为62.85%，通过设立弹性时间因子Δt为69.96 s，匹配乘客上车站点信息423 874条，匹配成功率为78.36%，提高了15.51百分点。部分上车站点识别数据如表1所示，2017年9月4日各公交站点客流量分布如图7所示。

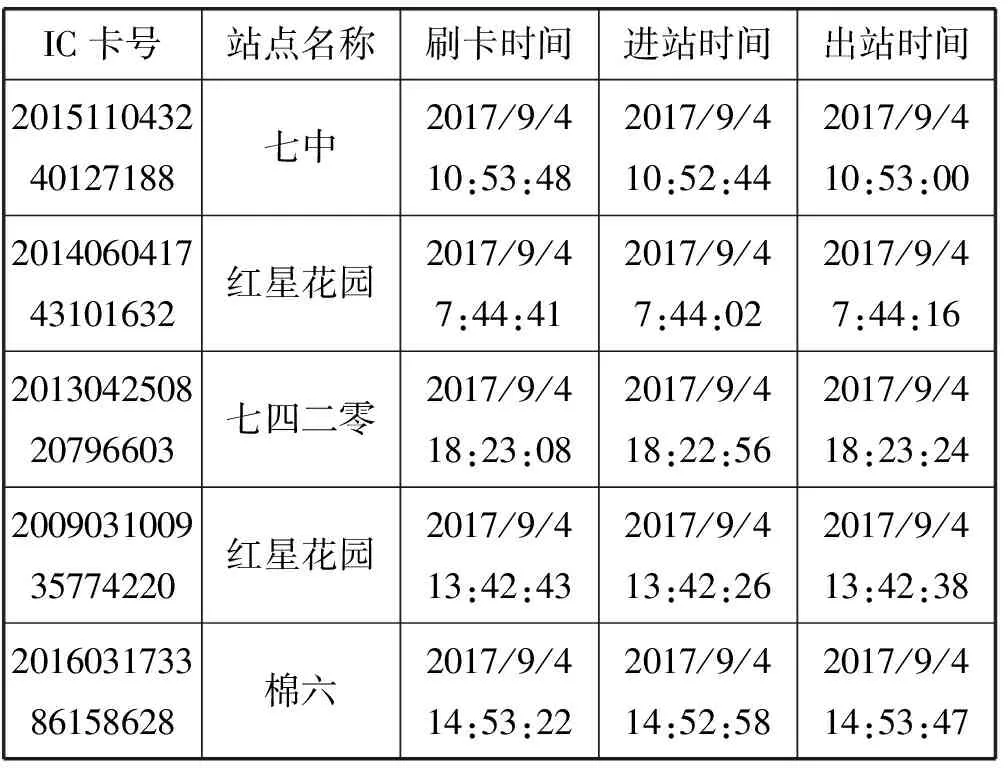
表1 部分乘客上车数据

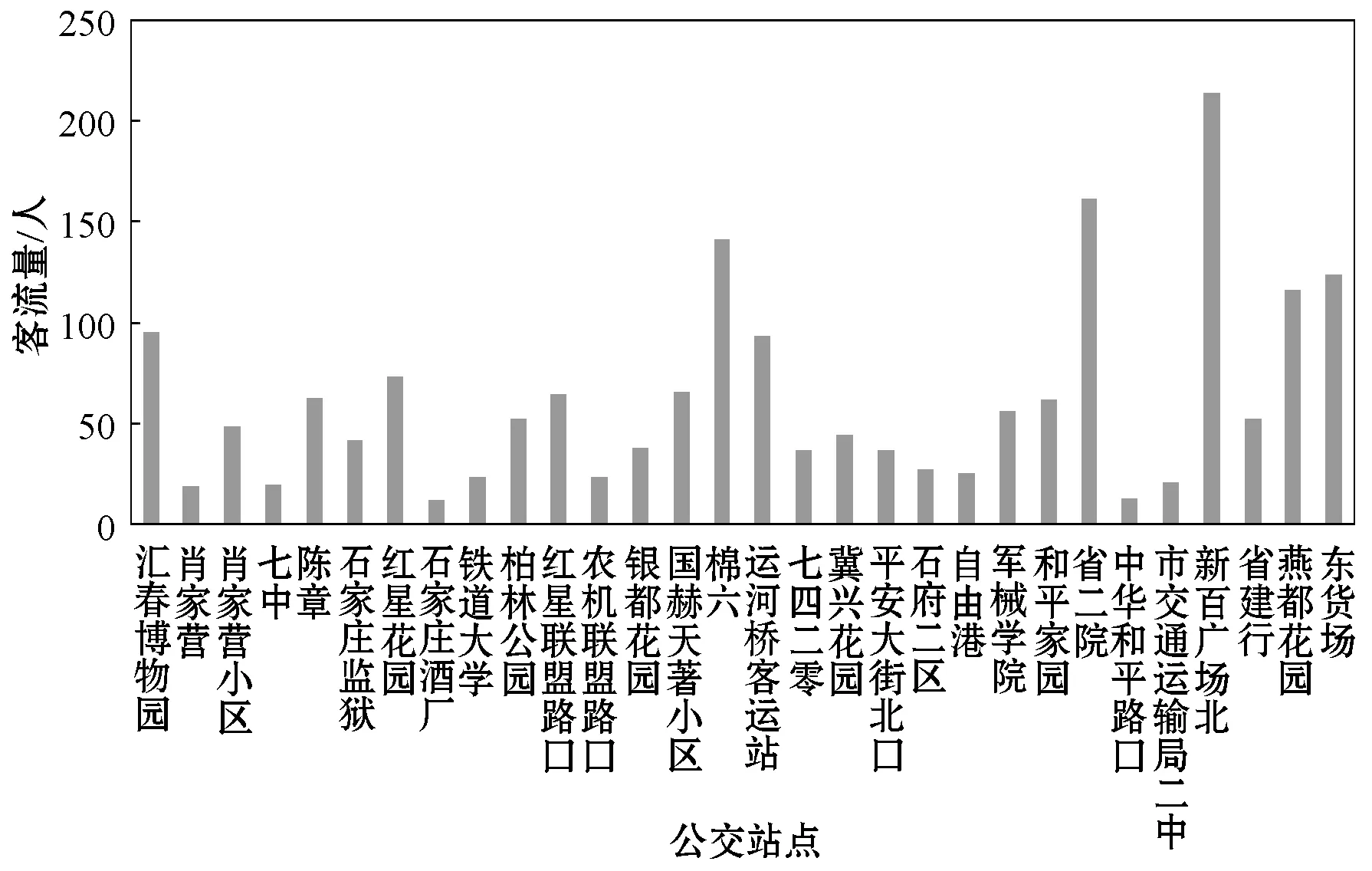
图7 23号线路公交站点上车人数分布

3.2 下车站点推断

以石家庄市23路公交线路为例，通过提出的公交站点吸引强度与公交出行链结合的方法，得到了2017年9月5日至7日的乘客OD出行数据。针对单体乘客，以CARD_ID为201410200117704476的乘客为例，该乘客公交出行OD数据如表2所示，可知该乘客居住在棉六附近，在省二院附近区域工作，该乘客平时乘坐101路与23路公交车完成公交出行过程。

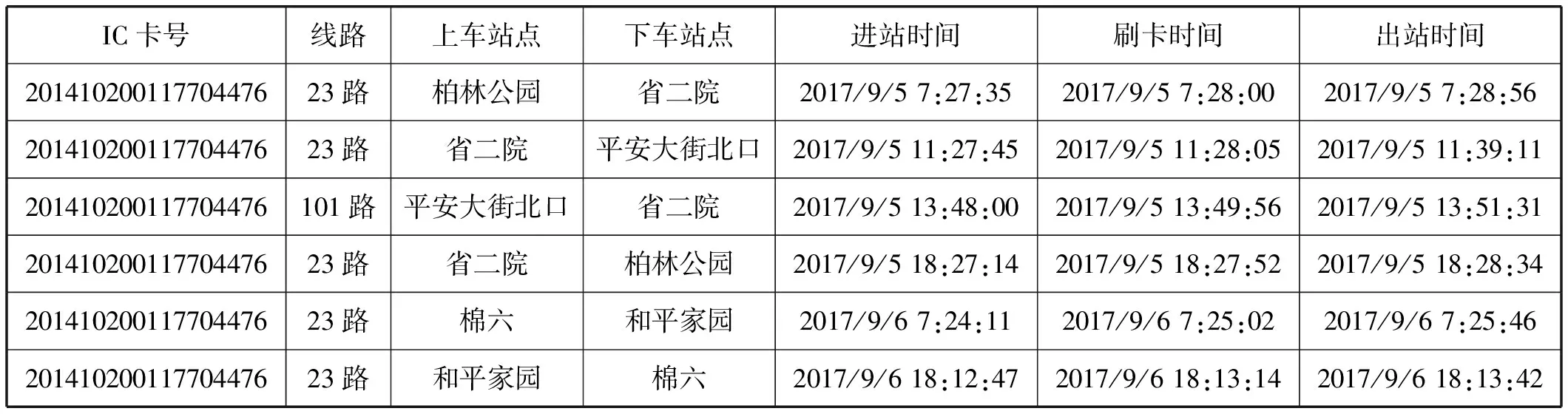
表2 乘客OD数据

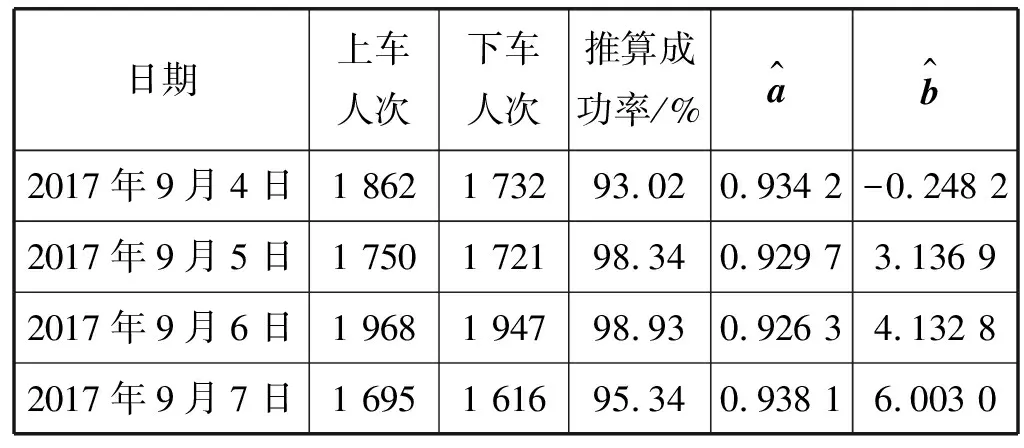
表3 回归参数分布表

结果表明，推算得到公交站点的客流产生量与客流吸引量在集计层面上是较为稳定的，可以较好地表达公交客流时空分布规律。

4 结 语

本文针对公交数据中乘客上下车站点未知的问题，在上车站点匹配方法中加入弹性时间因子，有效提高了乘客上车站点的识别率；在下车站点识别过程中，提取乘客下游站点集合与高频站点集合，以泊松分布理论为基础，从时间、空间角度研究了公交站点吸引强度的变化规律，提出公交站点吸引强度与公交出行链结合的下车站点推算方法。以石家庄市公交数据为例，对客流OD推算模型进行了有效性验证，结果表明：推算得到的公交站点客流产生量与客流吸引量在集计层面上表现较为稳定，所提出的OD推算方法有效可靠。