基于时频域行波全景波形的配电网故障选线方法

邓 丰 梅龙军 唐 欣 徐 帆 曾祥君

（长沙理工大学电气与信息工程学院 长沙 410004）

0 引言

我国中低压配电网广泛采用中性点非有效接地方式，在该运行方式下配电网发生单相接地故障（Single Line to Ground, SLG），存在故障电流较微弱、电弧故障不稳定、高阻接地故障等问题，使得基于故障信号稳态量的接地选线方法在实际应用时效果不理想。快速准确地选择故障线路，对保障电网安全稳定运行至关重要[1-5]。

基于行波的故障选线和电网保护及定位方法具有不受过渡电阻、电流互感器饱和、系统振荡及长线距离分布电容影响等优点，一直以来都是国内外继电保护领域的研究热点，专家学者对此开展了广泛而深入的研究。文献[6]利用各馈线不同频段的暂态故障信息，通过比较各馈线零序阻抗在高、低频段差异进行选线，选线准确率较高，但仅适用于配电网谐振接地系统。文献[7]针对现阶段故障选线算法经高阻接地及小故障初相位时选线效果不佳的问题，提出基于特征频带和数学形态谱的选线方案，但辨识母线故障和线路故障的运算过程复杂。文献[8]引入各条线路的相间相关系数与故障相的重心频率，计算故障特征距离作为选线判据，但人为设置阈值，导致母线经高阻接地故障时选线裕度不足。文献[9]基于暂态小波能量选线方法仅适用于纯架空线路，在架空-电缆混联配电线路中存在故障架空线路的能量比非故障纯电缆线路低而发生误判的情况。文献[10]提取暂态行波分量进行故障定位与选线。通过分析故障行波初始波头到达时差（Time Difference of Arrival, TDOA）矩阵的差值特征，实现故障选线，对本文具有一定参考价值，然而初始行波波头稍瞬即逝，准确提取波头受到各种因素的影响，选线可靠性有待提高。

针对现有选线方法存在的不足，本文提出一种基于时频域行波全景波形的配电网故障选线方法。行波全景波形[11]具有时间-频率-幅值和极性等丰富的时频域故障信息，运用S变换可真实、准确地展现故障线路和健全线路全景波形的特征差异。通过计算各条线路之间的相关系数之和，无需人工设置阈值，在3kΩ高阻接地故障下，仍能实现灵敏配电网故障选线。本文基于行波全波形多故障特征，选线效果显著优于仅基于局部故障特征的选线方法。大量仿真结果表明：本文算法不受中性点接地方式、故障过渡电阻、故障初相位和配电网出线形式的影响，原理简单，适应性强。

1 配电网选线原理分析

1.1 行波模量选择

当线路发生故障时，行波从故障点沿线路传播，由于相与相之间存在电磁耦合，导致各相线路行波传变特性无法独立分析。为此，本文采用Karenbauer变换进行解耦处理，将A、B、C相分量变换为相互独立的零模、α模和β模分量。本文将利用零模分量实现配电网选线，具体理由分析如下。

1）依据基尔霍夫电流定律，可以给出零模分量和线模分量的计算公式为

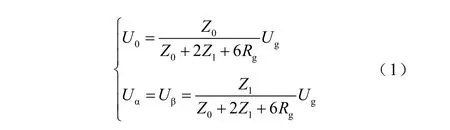
式中，Z0、Z1分别为零模和线模阻抗；Rg为故障过渡电阻；Ug为故障前故障点的电压。

由于零模阻抗大于线模阻抗，零模电压将大于线模电压，虽然零模分量比线模分量衰减快，但由于配电线路长度较短，所以在母线处的零模分量还是大于线模分量[12]。

2）对于配电网小电流接地系统，在零序通道中，均不会出现明显的故障或负荷工频电流，使得零模行波分量分辨率相对较高[13]，较易被提取，更适合构成故障选线判据。

3）当母线上装设电容补偿器时，线模分量以两相形成回路，受到补偿电容的影响。将补偿电容器等效为1/(ωC)，线模行波包含大量高频分量，并联电容器对高频分量相当于短路，线模行波大量存在于故障线路和电容器上，而健全线路上检测到线模行波信号较微弱。由于电容补偿器通常采用△或 0接线，零模行波在电容器内无法形成回路，其影响可忽略[12,14]，仿真结果如图1所示。

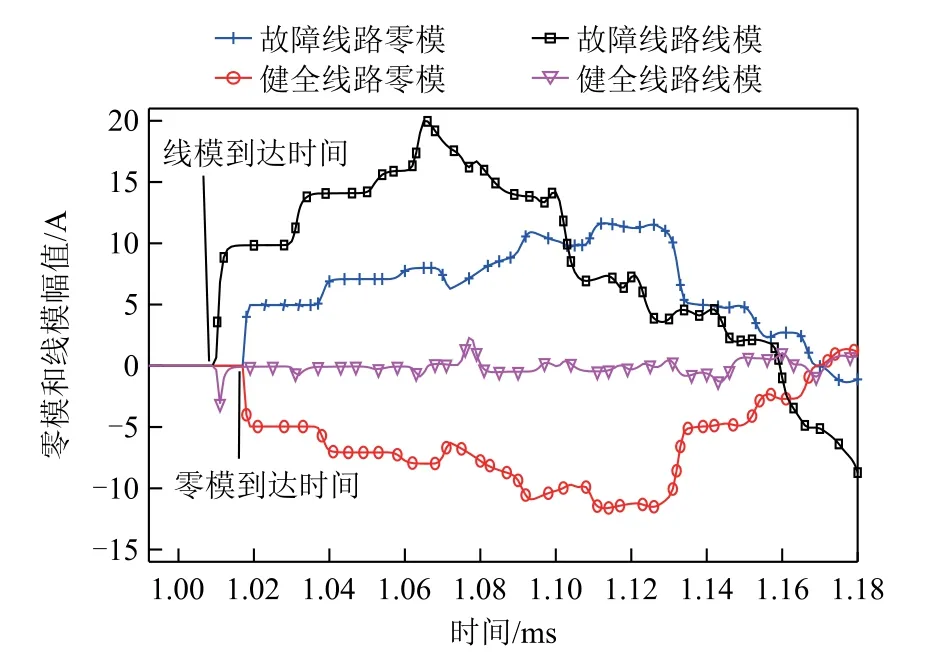
图1 存在母线并联电容器时故障线路与健全线路的 零模和线模波形Fig.1 Zero mode and line mode waveforms of fault line and healthy line with bus shunt capacitor

综合以上分析，从配电网选线的角度出发，选用零模分量更加合适。

1.2 故障行波全景波形

故障行波是一个宽频带阶跃信号，具有全时频特性[13]。从信号的角度分析，在时域上，行波波形是故障点产生的初始行波在波阻抗不连续点发生折射和反射后，各行波浪涌按照一定的时序叠加。故障点位置不同，线路参数不同，网络拓扑结构不同，折、反射过程不同，导致检测点检测到的行波幅值和行波波形形状差异很大。在频域上，依据叠加原理，行波波形既包含故障附加电源在网络中的暂态激励（其中含有大量的高频分量），同时也包含大量的低频分量，特别是工频分量。准确地说，故障行波是一个全频带信号，具有全时频特性。定义从检测到行波信号开始，选择某一时间窗T的波形，对该段波形进行S变换，从而绘制在时间窗T内故障行波时-频波形，如图2所示，称该波形为故障行波全景波形。

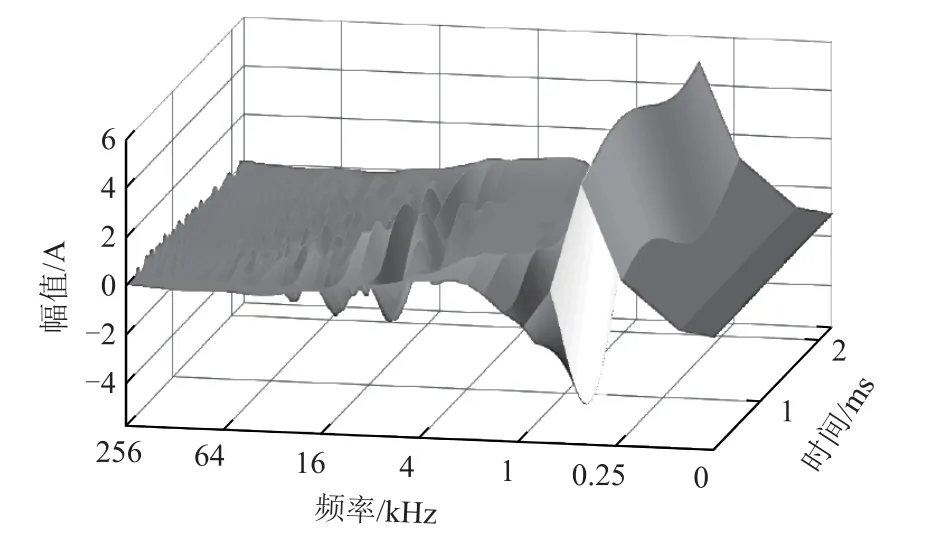
图2 故障行波全景波形Fig.2 Traveling wave panoramic waveform

如图2所示，时域的行波信号中蕴含了大量频域信息，这些信息中蕴含了丰富的故障信息，如故障点位置、系统拓扑结构、故障点参数（故障过渡电阻、故障初相位）等。故障线路和健全线路的行波全景波形具有不同程度的时-频相似性和差异性，深入挖掘宽频带行波全景波形的传输特性，可获得行波幅值、频率、极性等变化特征量，分析母线和线路不同故障点位置和故障参数下行波幅值、频率、极性的变化特性，可实现基于行波全景波形信息的配电网选线方法。

1.3 行波全景波形多特征差异性分析

1.3.1 行波幅值特征

当配电网发生SLG，故障线路可以看作故障前正常网络和故障网络的叠加，故障网络在故障点施加一个阶跃信号，初始电流零模分量i0的瞬时表达式为

式中，Uc为配电网正常状态下相电压的幅值；Rg为过渡电阻；φ为故障初相位。在确定的线路中，模阻抗Z0和Z1是确定的，可见，电流零模分量的幅值|i0|由故障初始相位和故障过渡电阻共同决定。

为进一步分析健全线路和故障线路行波幅值的差异性，以图3为例，配电网经消弧线圈接地系统发生SLG，故障相对地电压变为零，非故障相相电压升高为线电压。由于配电系统电路中，存在大量电力设备可等效为分布式电感电容等储能元件，发生SLG后，故障点突变电压会产生大量充、放电过程，产生故障行波。充、放电过程如图3所示。在线路L1中设置A相接地故障，UF为等效电压源，Rg为故障过渡电阻，CS为母线系统对地电容。

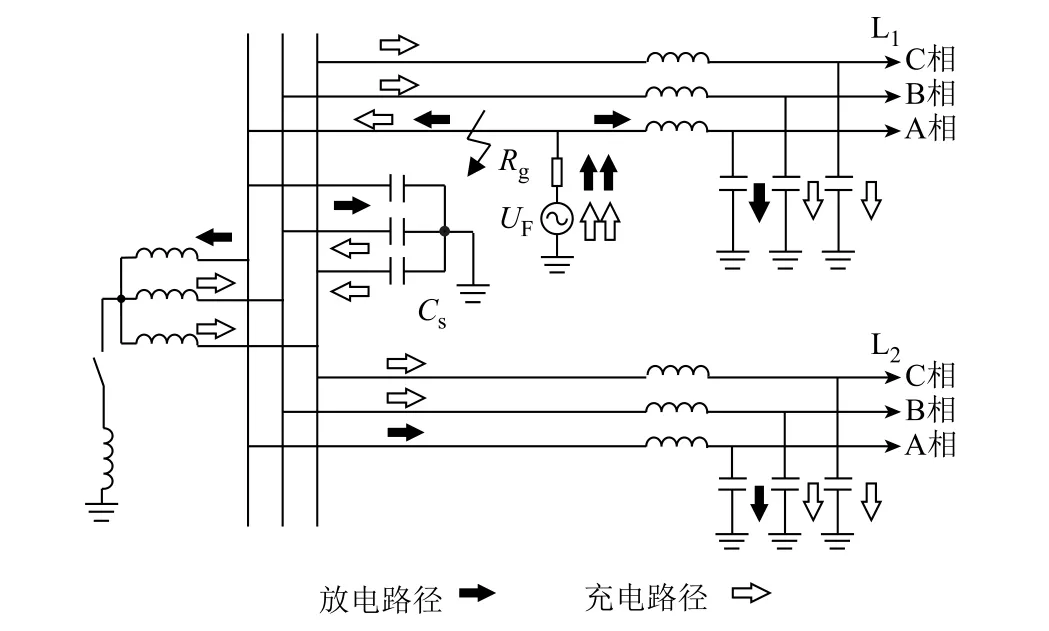
图3 单相接地充放电模型Fig.3 The charge-discharge model of single-line-toground fault

由图3可知，故障点产生的行波从故障点沿故障线路向健全线路传播，行波传播的过程实质是分布式参数（电容和电感）的放电过程和充电过程，具有以下特点：放电过程经故障线路电容与大地构成流通回路，回路电感小，信号衰减速度快；充电过程需通过母线系统（母线、变压器及母线上直接相连的高压设备），再经非故障线路电容与大地构成回路，整个回路电感大，信号衰减慢。

因此，故障线路行波幅值将明显大于健全线路行波幅值。

1.3.2 行波频率特征

配电网母线系统包括母线、变压器及母线上直接相连的高压电力设备，如互感器、刀开关、断路器等电力设备，深入分析故障行波全景波形在母线系统的幅频传变特性，可以得到故障线路和健全线路上传输的行波信号的频谱差异。

行波经过母线对地电容系统的行波折反射如图4a所示，波阻抗为Z11、Z22的均匀无损线路通过波阻抗不连续点K相连；电流波I1b为入射波，它从线路Z11向线路Z22传播时在波阻抗不连续点K处发生折反射。I1f为线路Z11上的反射波，由入射波在K点反射得到的；在线路Z22产生一个前行波I2f，称之为折射波。假定线路Z11、Z22均为无限长，根据彼德逊法则，在线路Z11上注入电压源2U1b，可得图4b所示的等效电路，推导出折射电流波I2f(s)为

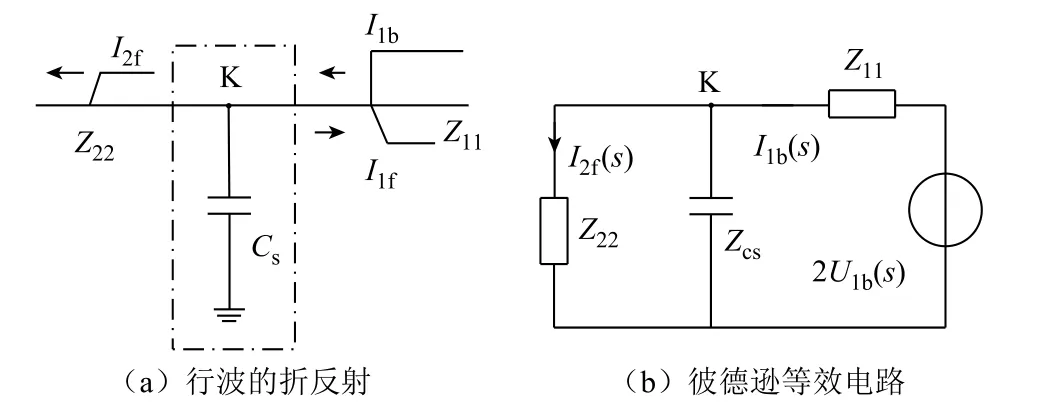
图4 行波经过母线对地电容系统Fig.4 Traveling wave passing through bus-to-ground capacitor system

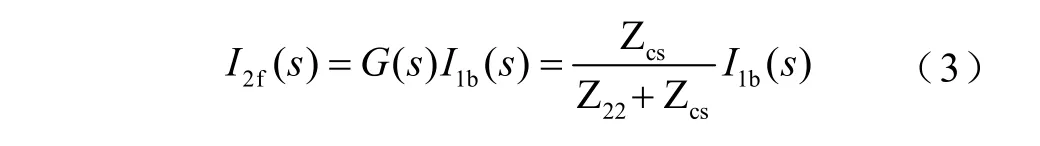
式中，G(s)为行波折射的传递函数，又称折射系数，与Z22、Zcs的大小相关。根据拉普拉斯变换，将复频域的变量s转换为频域的变量jω，可得到频域传输特性（折射系数）G(s)。文献[15-17]中母线系统对地电容CS可等效为 100～9 000pF，假设Z11=Z22=350Ω，则折射系数幅频特性如图5所示。

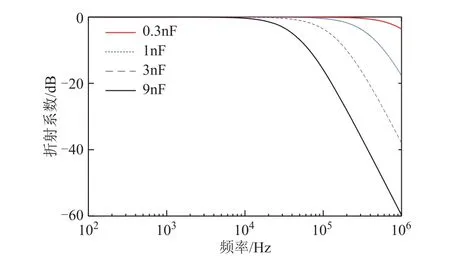
图5 母线系统折射系数幅频特性Fig.5 Amplitude frequency characteristics ofrefractive index

由图5可知，母线系统对10kHz以上的高频信号显著衰减，电容值越大，衰减作用越严重。因此，在故障线路上检测到的行波几乎是完整频带的波形，而传到健全线路上高频部分衰减严重。

此外，行波传播的过程产生的放电和充电：放电过程回路电感小，信号衰减速度快，振荡频率较高；充电过程回路电感大，信号衰减慢，振荡频率较低。

因此，故障线路行波信号频率要显著大于健全线路行波信号频率。

1.3.3 行波极性特征

在电力系统中，规定电流从母线流向线路为正方向。健全线路上行波传输方向为母线流向线路（正方向）；故障线路上行波传输方向为线路流向母线（反方向）。因此，故障线路与健全线路行波信号的极性完全相反。

综合以上分析，配电网小电流接地系统发生SLG时，故障线路和健全线路行波波形幅值、频率和极性存在很大差异性。因此，融合时频域行波全景波形中多个故障特征，设置选线判据，有望提高配电网选线可靠性。

2 算法实现

2.1 行波全景波形提取方法

S变换是一种具有强大时频分析能力的方法[18-20]，由短时傅里叶变换和小波变换的继承与发展而来。该变换算法最大的优点是具有无损可逆性与时频多分辨率性，引入了高斯窗函数，实现对时频分辨率的自适应性控制。随着高斯窗函数在时间轴上的移动，时域空间信号都被过渡到了频域空间，同时含有时域特性。因此，利用S变换分析非平稳零模信号i0(t)的过程中，可得到一个表征故障信息的时频域矩阵，其横坐标代表某一特征频率下信号随时间变化的分布，纵坐标代表某一采样时间下信号随频率变化的分布。

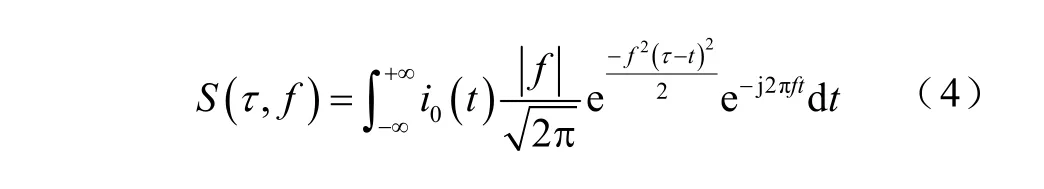
式中，t为时间；f为频率；τ为时间因子。时频域矩阵中包含大量与行波的时间、频率、极性和幅值有关的重要信息，S变换的结果也可用三维立体图表示，如图2所示，反映出行波信号真实的时间频率谱，完整地描述了各频率波形随时间变化分布的故障特征。

2.2 行波全景波形差异性量化分析方法

配电网发生SLG时，故障行波以时频域特性的全景信息进行传输。在频域上，将行波信号分解为M个频段，同时，将得到的每个频段的波形等分为N个时段，综合考虑不同时域下各频段信息，充分展现行波信号的局部时频特性，可得到众多时频小块，在频段j中时段i的能量谱小块计算式为

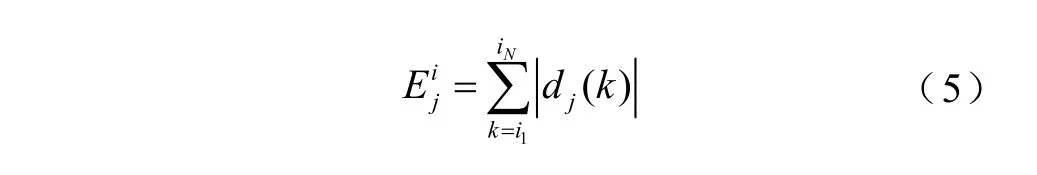
式中，i1和iN分别为采样点的起始和终止时间；dj(k)为对应频段j内，各采样时间点波形的实部幅值。借此，便可得到反映原始信号的时频谱矩阵EM×N为

基于统计学用协方差表征组数据变化趋势的思想，假设有两条不同的线路p、q，利用式（5）和式（6）可得到对应时频谱矩阵Ep与Eq，则两条线路的波形相似度[21-22]可进行描述，定义对不同线路Ep与Eq互相关性rpq为

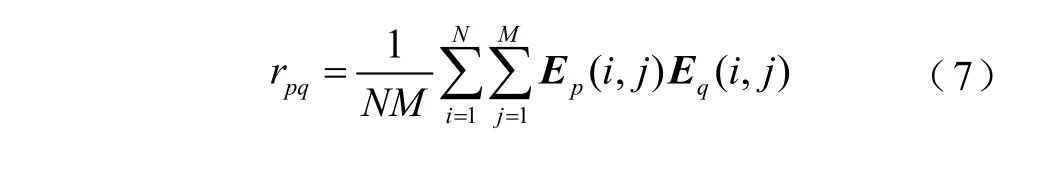
式中，Ep(i,j)、Eq(i,j)分别为线路p、q时频谱矩阵第i个频率所对应的第j个时段元素。对不同线路Ep与Eq方均根值表示为

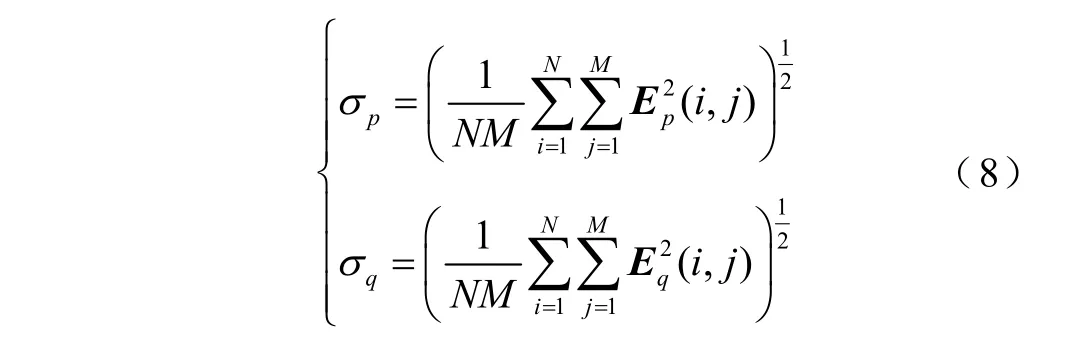
进一步对式（7）、式（8）进行归一化处理，可得到处理后的相关系数公式为

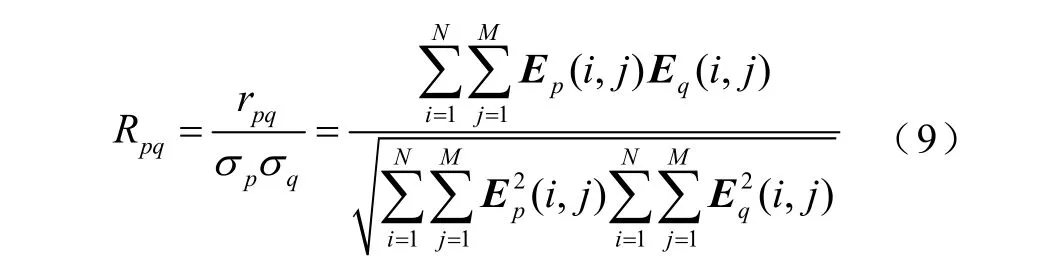
式中，Rpq为两线路之间电流行波零模分量波形相似度的相关系数，且Rpq∈(-1,1)，其中正负号表示相关的方向。Rpq的绝对值越接近1，说明两条线路的相似程度越高；Rpq的绝对值越接近0，说明两条线路的相似程度越低。当配电线路发生故障时，健全线路间的电流行波零模分量波形相似度正相关；而故障线路与健全线路电流行波零模分量波形相似度负相关。此外，波形相似度算法最大优点在于对轨迹的变化趋势有很强的识别能力，能充分计算出轨迹的形态，同时不受幅值大小的影响。

2.3 故障选线方法

利用S变换得到一定时间窗内故障行波全景波形，构造出时频谱矩阵EM×N；利用波形相关系数，量化分析每条线路检测行波全景波形的相似性和差异性，进而形成配电网选线判据，实现配电网可靠、准确选线。故障选线流程如图6所示。

图6 故障选线流程Fig.6 Algorithm flow chart of fault line selection

具体实现算法步骤如下：

1）每条线路母线出口处安装行波采集装置，检测每条馈线上的电流行波信号。

2）对各条线路电流行波信号进行Karenbauer（凯伦贝尔）变换，获得电流行波零模分量i0。

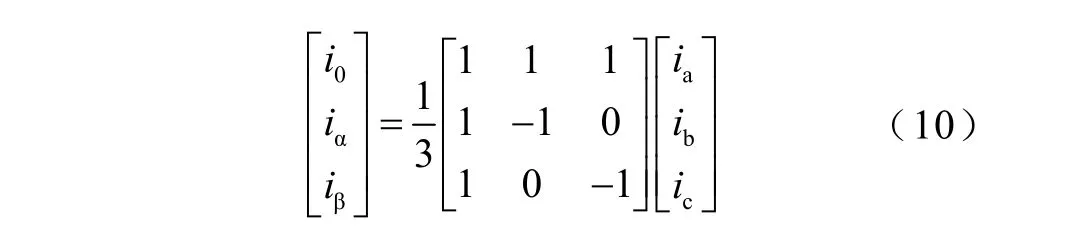
式中，iα、iβ为线模电流；i0为零模电流，ia、ib、ic为相电流。

3）利用S变换对各条线路的电流行波零模分量i0进行时频域分析，得到从初始行波波头到达检测点后，一定时间窗内故障行波全景波形，进而得到各条线路的时频谱矩阵EM×N。

4）对各条线路时频谱矩阵EM×N进行两两相关性分析，得到相似度关联系数矩阵R为

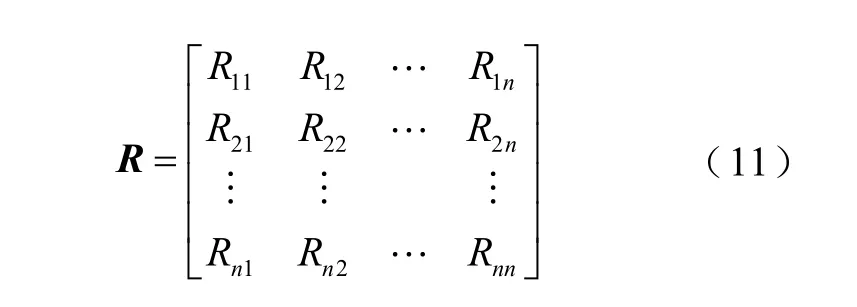
式中，i为线路编号，i=1,2,…,n。求出相似度关联系数矩阵R中每一行矩阵元素之和，得到各条线路的综合相关系数Ri，即

式中，Ri为第i条线路综合相关系数之和；Rij为线路i与线路j之间的相关系数。

值得一提的是：通过求解矩阵中每行元素之和Ri，以Ri作为每条线路的综合相关系数，可在一定程度上放大故障线路与健全线路的差异性。

5）根据综合相关系数矩阵RT中各元素之间的极性与幅值关系，形成故障选线判据，即

若满足式（14），第i条线路的综合相关系数最小，且与其他n-1条线路的正负极性相反，则判定第i条线路为故障线路，其他线路为健全线路。

6）根据综合相关系数矩阵RT中各元素之间的极性与幅值关系，形成母线故障判据，即

若满足式（15）则判定母线故障。

3 仿真验证

3.1 仿真模型

在仿真软件ATP/EMTP中建立10kV配电网系统的仿真模型如图7所示，在Matlab中进行数据处理，验证作者所提配电网故障选线方法的可行性。配电网模型采用四条不同供电方式的线路，分别为L1纯架空线路、L2纯电缆线路、L3混联架空-电缆线路和L4含有分支的架空线路，线路参数见表1[12]。变压器为110kV/10.5kV，低压侧中性点采用经消弧线圈接地方式，线路上负载均用100+j6.282Ω阻抗来模拟，母线系统对地等效电容CS取1μF，消弧线圈补偿度X取8%，系统对地电容并联之和为C∑，从而计算出消弧线圈中电感L为

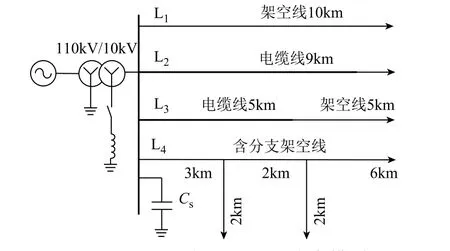
图7 10kV配电网EMTP仿真模型Fig.7 EMTP simulation model of 10kV distribution network

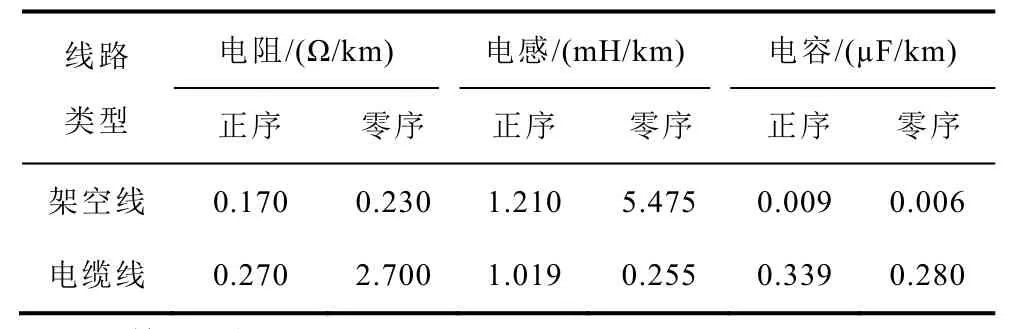
表1 配电网10kV线路参数Tab.1 Parameters of 10kV line in distribution network

3.2 仿真分析

仿真分析中采样频率取1MHz，在考虑充分展现故障行波全景信息，但又不影响算法计算速度的情况下，截取初始行波波头到达后100μs时间窗内的行波全景波形。本文针对不同故障点位置：架空线路故障、电缆线路故障、线缆分接头故障、分支节点故障、母线故障等情况下发生SLG，设置过渡电阻Rf=500Ω，初相位θ=15°时，进行大量仿真分析，选线结果见表2。从表2中可知，本文选线算法对不同故障位置均具有良好的效果。

表2 基于不同故障位置的仿真结果Tab.2 Simulation results based on different fault locations

4 选线方法适应性分析

4.1 中性点不同接地方式的影响

配电网小电流接地系统中性点接地方式可分为：经消弧线圈接地、经电阻接地和不接地三种方式。由于不同的中性点接地方式，整个回路的电感不同，对电流行波零模振荡频率具有一定的影响。本算例设置不同的系统中性点接地方式，在线路L3和L4不同位置模拟SLG，过渡电阻Rf=1kΩ，初相位θ=15°，选线结果见表3。仿真结果表明，对于不同中性点接地方式，本文算法均可靠动作。

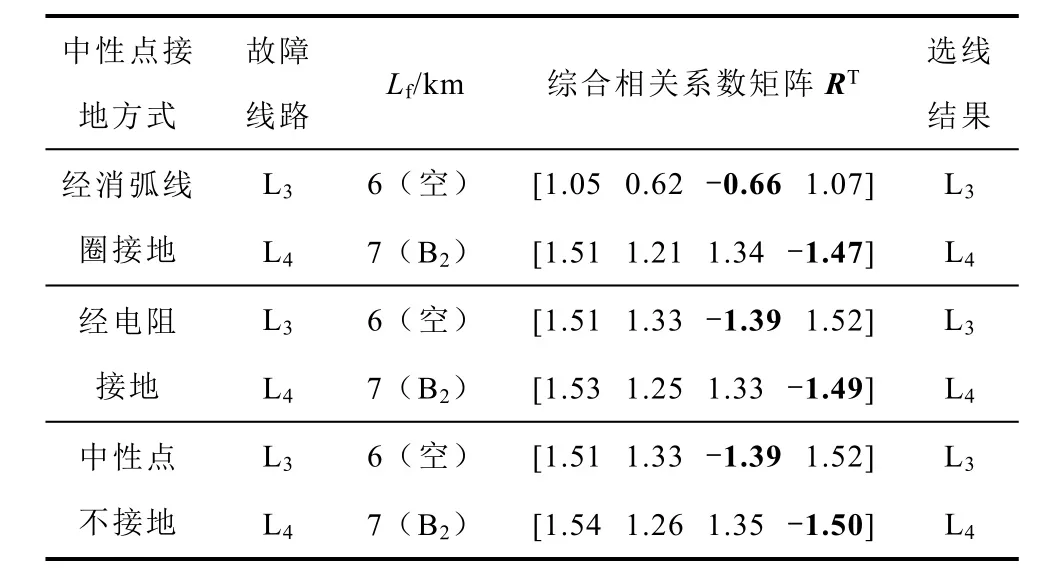
表3 基于中性点不同接地方式的仿真结果Tab.3 Simulation results based on different neutral grounding modes

4.2 补偿度不同的影响

在消弧线圈接地系统中，由于感性消弧线圈过补偿作用，可抵消接地故障的容性电流，使得系统故障电流减小，其中消弧线圈的补偿度X不同时，电流减小的幅度会存在差异。本算例模拟线路L3在不同位置发生SLG，过渡电阻Rf=1kΩ，初相位θ=15°，仿真分析结果见表4。结果表明，经消弧线圈接地系统中消弧线圈不同补偿度对本算法无影响。

表4 基于不同补偿度的仿真结果Tab.4 Simulation results based on different compensation degrees

4.3 线路末端高阻接地的影响

当线路末端过渡电阻Rg过大，故障初相位θ偏小时，检测到行波电流零模分量i0幅值较小，对实现精准可靠的故障选线具有一定挑战。在线路L1末端处设置SLG，故障过渡电阻Rf=3 kΩ，设置不同故障初相位，验证本文选线方法的适应性，仿真结果见表5。从表5中可看出：线路末端发生高阻接地故障时，随着故障初相位的降低，波形相关系数的差异性略微减小，但本文运用波形相似度原理，不受波形幅值大小的影响，矩阵RT中故障线路与非故障线路对应元素的极性和幅值具有明显的差异，仍可实现可靠故障选线。

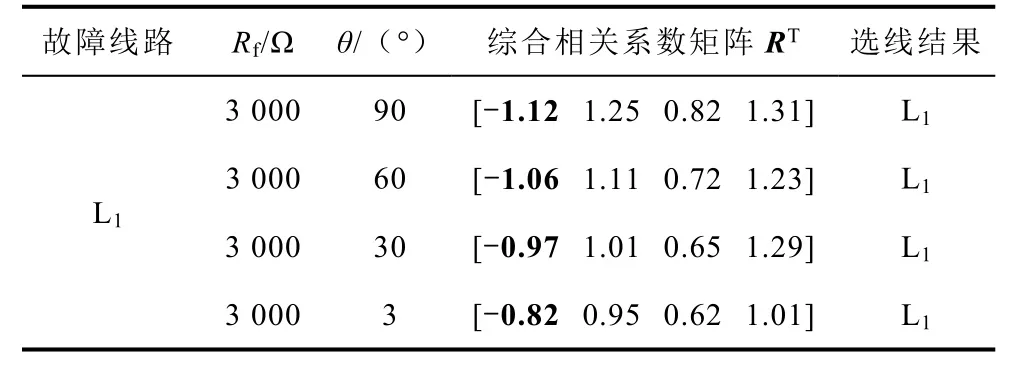
表5 基于线路末端高阻接地的仿真结果Tab.5 Simulation results based on high resistance grounding at the end of line

4.4 瞬时电弧接地的影响

间歇性弧光接地是一种常见故障，其不稳定燃弧过程复杂，作者依据电弧接地现象及电弧特征，在ATP/EMPT仿真软件搭建Mayr电弧模型，其表达式为

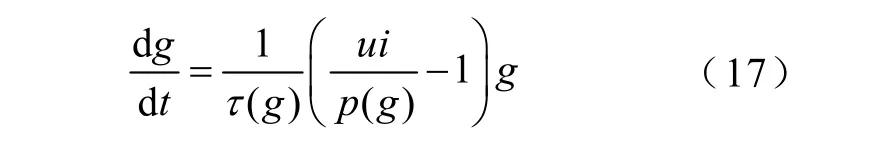
式中，u为电弧电压；g为电弧电导；i为电弧电流。它们均为时间t的函数。p(g)为电弧散热功率；τ(g)为电弧时间常数，它们均为g的函数。电弧能否持续燃烧的关键变量是电弧散热功率p(g)与电弧时间常数τ(g)，通过控制p(g)与τ(g)变化，实现电弧熄灭与重燃特性。模拟架空线路L1在Rf=30Ω，初相位θ=90°时发生的电弧接地故障，选线结果见表6。计算结果表明，本方法在瞬时电弧故障下具有良好的选线效果。

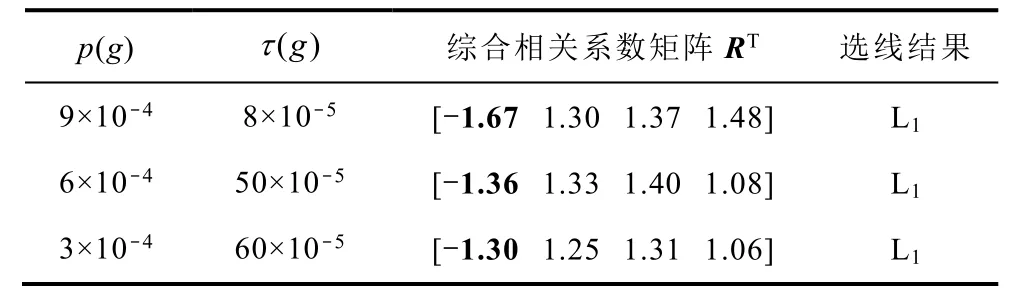
表6 基于电弧故障的仿真结果Tab.6 Simulation results based on arc fault

4.5 母线并联补偿电容器的影响

配电网母线上一般都接有电容器进行无功补偿，母线上并联的补偿电容器，一般接成三角形或不接地的星形。本算例在母线并联不接地的星形电容器情况下，模拟线路L3和L4不同故障位置发生SLG，故障过渡电阻Rf=1kΩ，初相位θ=15°，仿真结果见表7。从表7可以看出，本算法适用于母线并联电容器的配电网。

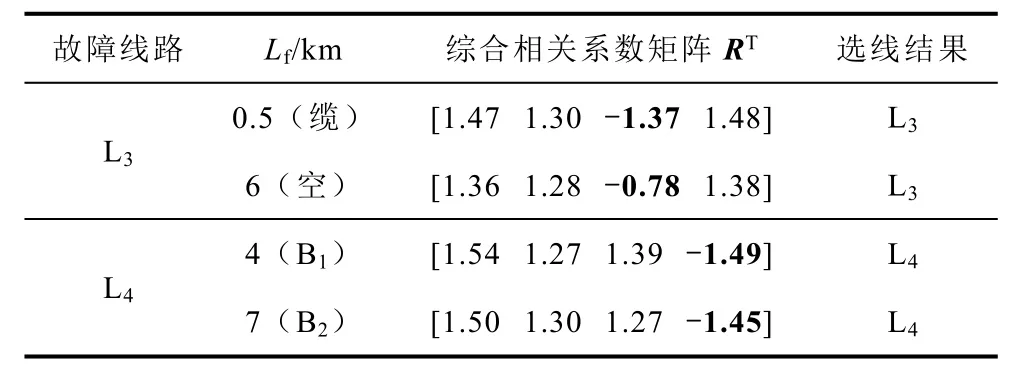
表7 基于母线并联补偿电容器时仿真结果Tab.7 Simulation results based on bus shunt capacitor

4.6 时间窗不同的影响

选取不同的时间窗，行波全景波形所包含的时-频数据不同，波形相关系数会发生改变。分别在线路L3和L4不同位置设置SLG，故障过渡电阻Rf=1kΩ，故障初相位θ=15°。仿真结果表明：时间窗选取较长时，由于电流行波后续大量折反射波形衰减严重，各条线路行波全景波形差异性降低，但正负相关性始终保持不变，时间窗选取较短时，只要行波全景波形中蕴含足够丰富的故障信息，时间窗取0.1ms情况下，仍然可以保证准确、可靠故障选线。

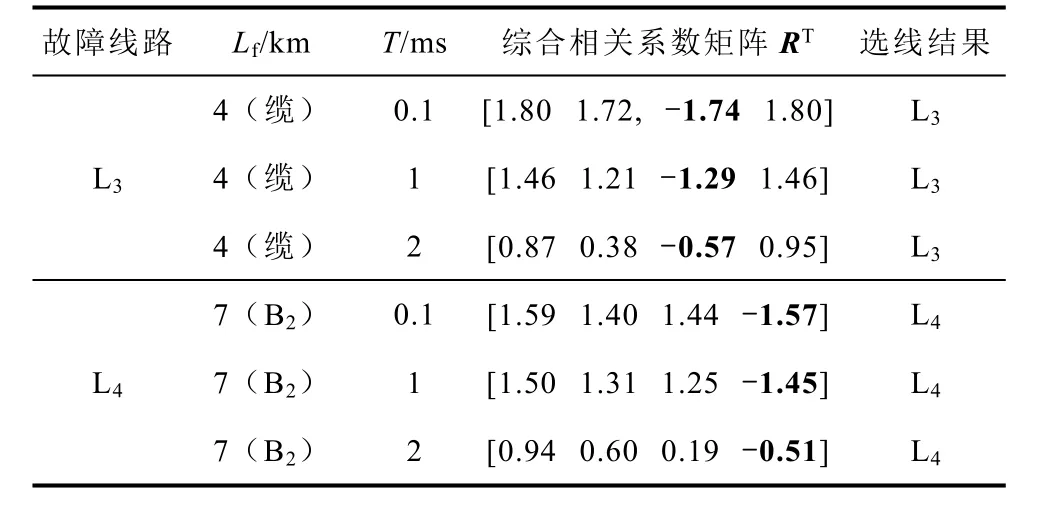
表8 基于不同时间窗的仿真结果Tab.8 simulation results based on different time periods

5 结论

本文根据故障线路和健全线路电流行波零模分量时频域全景故障特征差异性形成选线判据，通过理论分析和大量仿真算例，得到如下结论：

1）利用行波全景波形时间-频率-幅值-极性多维度特征信息进行故障选线，可有效提高故障选线方法的可靠性，为配电网故障选线难题提供了一种新思路。

2）故障选线算法仅检测100μs时间窗故障电流行波波形，即可实现可靠配电网选线，动作速度快。

3）算法无需人工设置阈值，计算各条线路综合相关系数Ri，可在一定程度上放大故障线路与健全线路的差异性，通过判断矩阵RT元素中极性和幅值关系，实现灵敏配电网选线，算法原理简单。

4）算法不受中性点接地方式、瞬时电弧接地、故障过渡电阻、故障初相位和配电网出线形式的影响，在3kΩ高阻接地故障下，仍能实现灵敏配电网选线，算法适应性较强。