多无人机对组网雷达的协同干扰控制策略研究*

何 嘉， 奚峥皓,2， 阚 秀， 王汉东， 沈 颉

(1.上海工程技术大学 电子电气工程学院，上海 201620；2.清华大学 计算机系智能技术与系统国家重点实验室，上海 201620)

0 引 言

雷达作为战争中有效监控识别工具，围绕其展开的电子对抗一直受到广泛关注[1,2]。组网雷达可以构成多层次、全方位、立体化的空间监控网络[3～5]，实现对敌方目标及干扰假目标的识别，这也使得传统的对单一雷达的欺骗策略失效[6,7]。在这种情况下，采用多电子战飞机(EWA)协同工作干扰组网雷达已成为热点研究问题[8]。

针对多EWA协同干扰组网雷达问题，Pachter M等人[9]总结了多EWA协同干扰欺骗组网雷达问题中的概念。Mears M J等人[10]引入了一代价函数描述EWA的运动状态，对EWA和假目标进行航迹优化，但算法只考虑了二维平面的情况。李飞等人[11]给出了三维空间中EWA的协同干扰控制算法，但算法是在固定起、终点的情况下进行解算，而现实中往往无法确定终点位置。

本文综合以上分析，根据EWA和组网雷达的工作特性，并从节省战争资源和成本的角度出发，提出一种新的多EWA协同控制策略实现对组网雷达的有效干扰，即使用尽可能少的EWA以尽可能少的操作步骤完成欺骗任务，并通过数据进行仿真实验，验证算法的合理性和有效性。

1 原理与假设

1.1 有源假目标欺骗原理

雷达的工作原理是根据其发射信号的回波解算目标的速度与距离。在实际应用中，为了实现对目标的精确定位，雷达通常是周期性定向工作，因此对于某一方向而言，雷达的发射信号呈周期性变化，EWA正是基于周期信号回波的延时或提前的特点实现对雷达的距离欺骗。

如图1，EWA通过机载干扰器延迟或提前干扰雷达的发射信号并发射回去，使雷达接收回波后得到假目标。若已知EWA到雷达的距离为r，假目标到雷达的距离为R，雷达周期为Tp，其时延Δt可以表示为

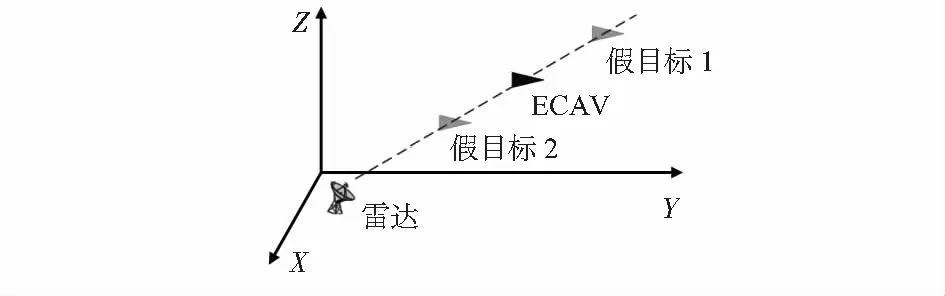
图1 有源假目标欺骗示意

(1)

1.2 组网雷达识别原理

鉴于单一雷达容易受到欺骗，组网雷达已成为现代战争中实现监控识别的一种必然手段。在组网雷达的探测中，对于真实目标的校验通常是通过“同源检验”，即目标在各个雷达分站中的空间状态基本一致。

分布式组网是一种常用的雷达组网方式，其工作核心在于航迹关联检验。各雷达将探测数据传输给数据融合中心，数据融合中心将所有数据结果标记在同一空间坐标系中，依据同源检验的原理对数据进行分析。并设定合适的的门限值，校验航迹发生的可行性，得到最终的航迹融合信息。

1.3 背景假设

地面分布式组网雷达由5个雷达构成P={A1,A2,A3,A4,A5}。所有雷达的最大作用半径均为150 km，且数据更新速率为10 s/次。组网雷达满足如下数据融合规则：同一时刻，至少3部雷达在空间中同一位置检测到目标时，数据融合中心通过目标的同源检验，并将此位置确定为一个合理的航迹点。连续20个航迹点构成一目标航迹，并将其视为一条真实的目标航迹。

5个雷达具体的位置坐标为A1=(80,0)，A2=(30,60)，A3=(55,110)，A4=(105,110)，A5=(130,60)(km)。

根据EWA和组网雷达的工作原理，本文模型建立和计算满足如下假设条件：1)EWA的飞行速度在120～180 km/h，飞行高度控制在2 000～2 500m，最大加速度不超过10 m/s2；2)EWA可被视作为质点；3)EWA自身不会被雷达探测到，而干扰设备的欺骗信号一定能被有效探测到；4)同一时刻同一架EWA只能干扰一部雷达，可在雷达与EWA的连线及延长线上产生多个假目标；5)所有设备均运转正常，无数据误差。

2 模型与求解

2.1 单一EWA工作

图2为单一EWA实现对雷达距离欺骗时的空间关系。

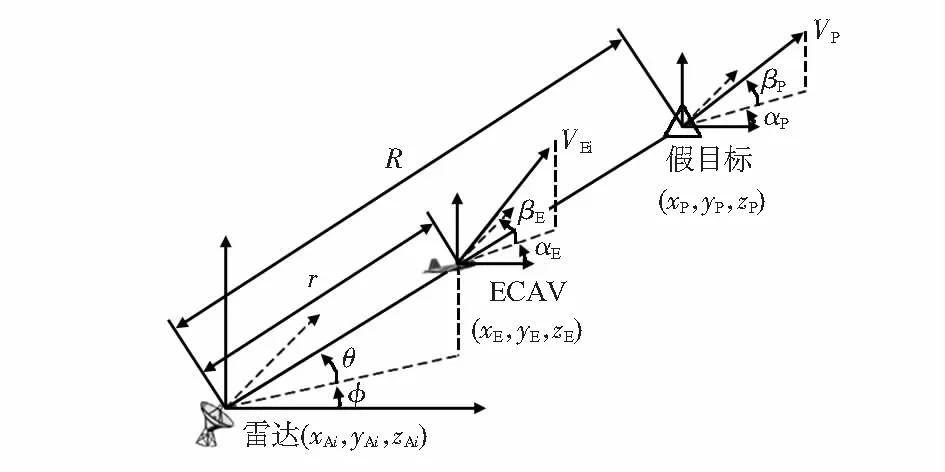
图2 单架EWA对地面雷达干扰示意

图2中，(xAi,yAi,zAi)为地面雷达Ai的空间坐标;(xE,yE,zE)为EWA的空间坐标;(xP,yP,zP)为假目标P的空间坐标;φ为EWA与雷达连线的方位角;θ为EWA与雷达连线的倾角;αE为EWA的飞行方向角;αP为假目标的飞行倾角;βE为EWA的飞行方向角;βP为假目标的飞行倾角;vP为EWA的飞行速度;vP为假目标的飞行速度;r为EWA到雷达的距离;R为假目标到雷达的距离。

生成的假目标运动状态满足

(2)

雷达捕捉到的假目标运动关系满足

(3)

对式(3)进行求导并写成矩阵形式，可得

(4)

其中

将式(2)代入式(4)可得

(5)

同理，EWA的运动状态满足

(6)

(7)

(8)

且ECAV的速度为

(9)

综上所述，由式(2)～式(9)可完整描述单一EWA欺骗单一雷达的工作过程，并给出运动参数。

2.2 多EWA模型建立

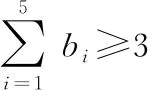
组网雷达中，单架EWA无法在短时间内欺骗多个雷达，若想用最少的EWA达成目的，就需要使其飞过尽可能多的假目标投影点。因此，可将问题离散化，转化为路径规划问题[12,13]。此时，多EWA协同干扰组网雷达的控制问题可以简化为求解：1)在假目标到指定雷达的投影空间中，确定飞过所有投影点所需要的EWA数量；2)在确定EWA数量下，飞过所有投影点的EWA最优控制策略。

在单一雷达投影空间中，所需要的最少EWA数量n满足如下优化模型

minn

(10)

式中 5个约束条件分别对应限定了EWA的速度、飞行高度、最小间距、转弯半径和加速度。

然而，最优化模型式(10)所能得到的EWA飞行航迹并不唯一。在实际飞行操作过程中，有vE,αE,βE三个自由度，对应这三个自由度建立如下操作复杂度函数

(11)

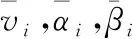
s.t.Vmin≤vE≤Vmax,hmin≤rsinθ≤hmax,

D≥Dmin,Dmin=100 m,RT≥RTmax,a≤amax

(12)

在EWA高度不变的情况下倾角βE=0，仅需要操控速度与方向角，是理想的操作环境，此时方向角与速度为

(13)

上式即EWA在固定高度下的运动模型。

2.3 模型求解

对于式(10)以及式(12)所提出的最优化模型，从求解效率和精度两个角度出发，本文分别采用了广度优先搜索(BFS)算法和禁忌搜索(TS)算法。

对于式(10)模型，其目的在于使用尽可能少的EWA飞过干扰信号连线投影点，求解以效率为主，此时采用BFS算法可以达到快速求解的目的，BFS算法针对单个雷达，判断一架EWA飞过所有干扰信号连线投影点的可行性，如果可行则欺骗成功，不可行则考虑其余4个雷达。

对于式(12)模型，其目的在于在限定飞行空间内寻求最少操作步骤完成欺骗，即求得EWA的协同控制策略，采用TS算法可以获得空间内全局最优的解航迹。为便于求解，将假目标的空间投影离散化，即，在约束的飞行高度内，将飞行空间划分为n个平面δ1,δ2,…,δn，并在这n个平面上求解假目标的投影点，针对单个雷达求得其捕获假目标所形成的 个航迹离散点，并以此作为TS算法的搜索空间，初始值为BFS算法求得的解。

完整的模型求解过程如下:1)构建组网雷达模型；2)构建EWA运动模型；3)选定雷达 ，在该雷达方向上离散化假目标航迹投影点；4)用BFS算法求解能否使用单架EWA完成目标；5)若能，将步骤(4)的解作为初始解，用TS算法求解最优控制；6)若不能，返回步骤(3)重新选择雷达。

融合航迹校验，是否能完成已知假目标航迹，若能，输出所有EWA飞行航迹。

3 实验验证与分析

如表1所示，表中给定了一段已知连续假目标航迹，求解实现此假目标航迹的EWA的协同控制策略。

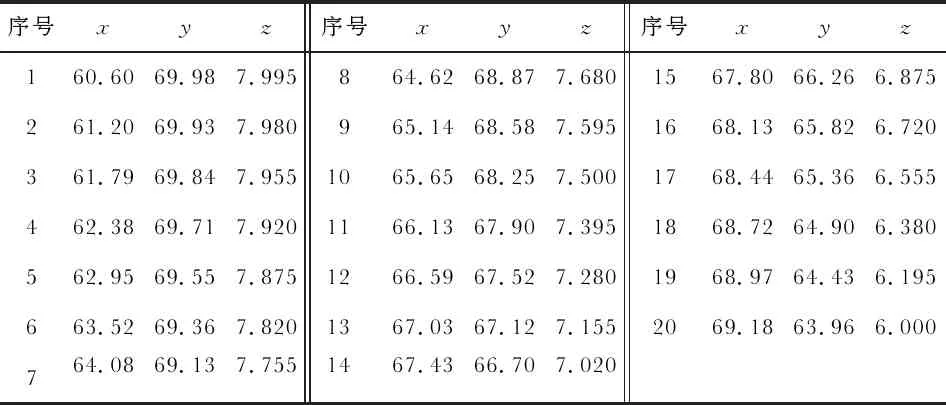
表1 已知假目标航迹点 km

表2给出了2 500 m高度平面上5个雷达方向上的投影点到下一投影点所需飞行速度，根据假设条件，EWA的最大飞行速度为180 km/h，因此，在平面上使用单架EWA无法完成所有假目标投影点的飞行，需要在空间中求解EWA的飞行参数。

表2 2 500 m高度平面上投影点速度 (km/h)

使用BFS算法和TS算法求解模型式(10)与模型式(12)，得出使用三架EWA可以协同完成给定假目标航迹的欺骗行为。以1号EWA为例，在表3中给出了其求解出的完整协同控制策略。且其对应的空间轨迹，通过作图的方式显示在图3中的(a)图中，与表3中的数据一一对应，构成了1号EWA在空间中为形成目的假目标轨迹所需要的全部控制参数。而图3中(b)与(c)则分别为2号EWA与3号EWA在空间中的轨迹。

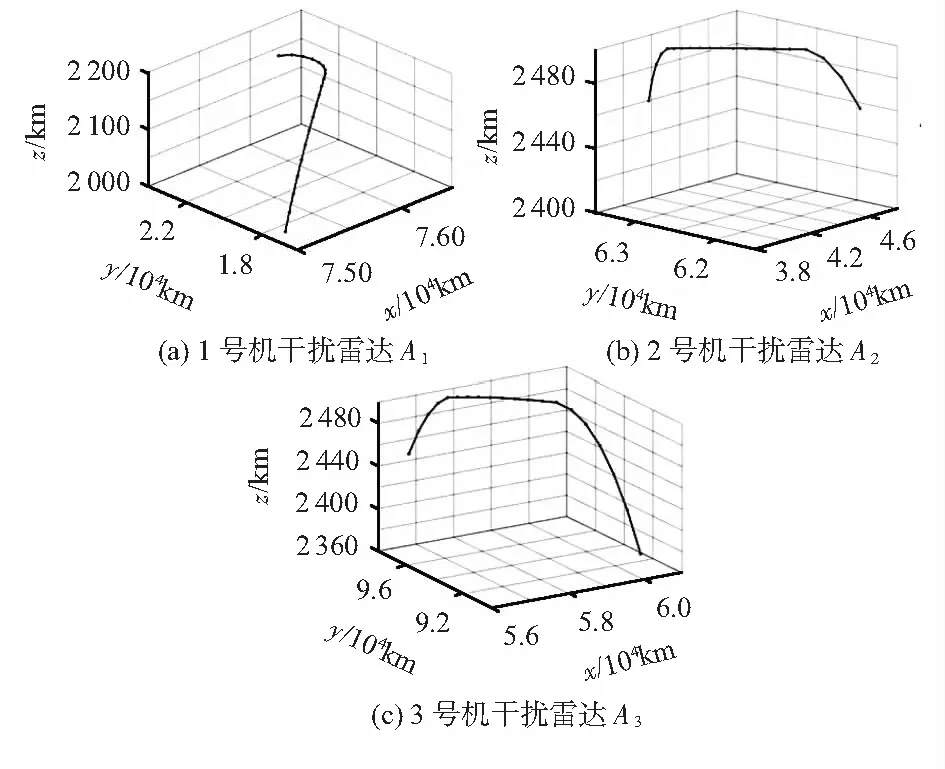
图3 各EWA干扰雷达的航迹

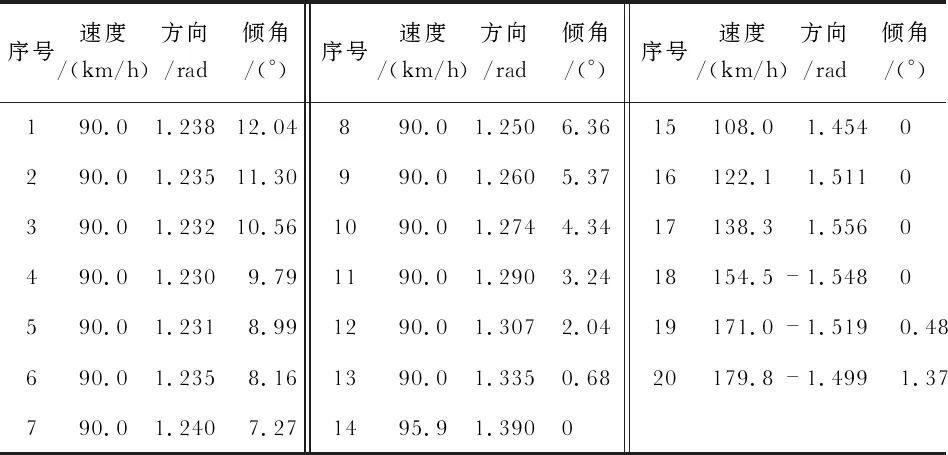
表3 EWA的协同控制策略

在图4中，给出了三架EWA对应的飞行速度、方向角和倾角的曲线图，从图4中结果可以看出，所有飞行路径均符合运动模型，满足实际约束条件。结果完全符合实际要求，且满足使用尽可能少的EWA在尽可能少的协同操作下完成给定假目标航迹的飞行，所有飞行航迹均为光滑曲线，因此本文所提出的算法在非周期组网雷达中亦可拥有较好的应用效果。

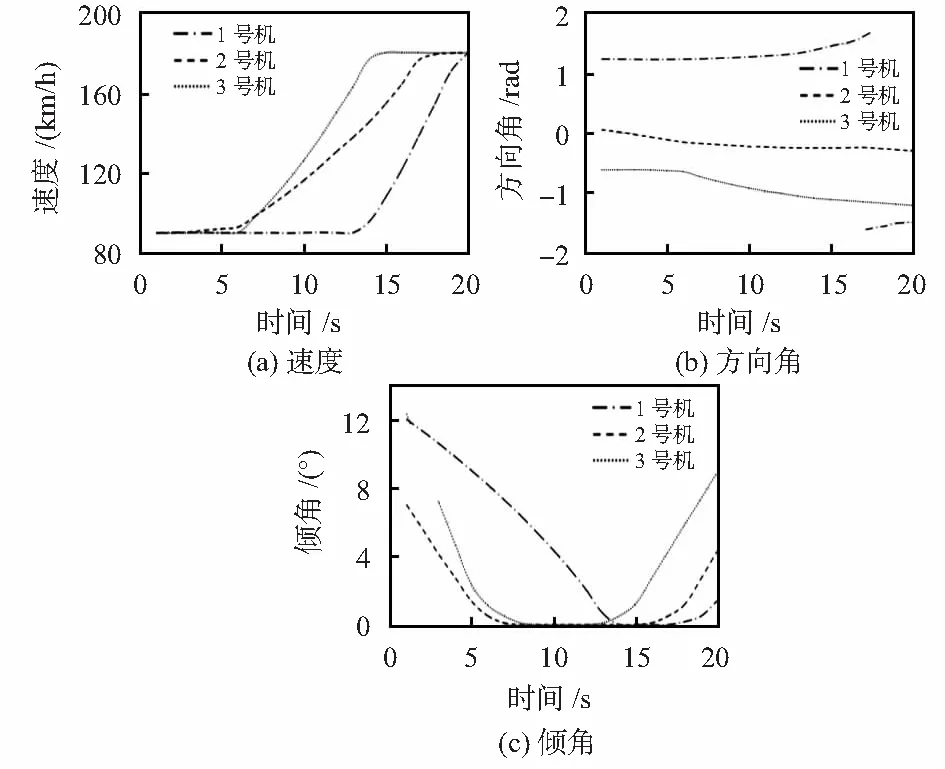
图4 EWA参数分析

4 结 论

本文根据EWA的工作原理和采集到的组网雷达信息，建立多EWA协同干扰组网雷达的最优控制模型，采用BFS算法和TS算法对模型进行求解，给出以最少数量的EWA和最少的协同操作步骤完成对组网雷达的欺骗的最优控制策略。在给定假目标航迹数据的条件下，给出对应的实际EWA最优飞行策略，验证了本文模型的合理性和求解方法的有效性。