面向聚变堆维护的重载机械臂CMOR运动学算法设计及仿真
赵中旭,潘洪涛,程 勇,樊玉琦
(1.合肥工业大学 计算机与信息学院,安徽 合肥 230009; 2.中国科学院等离子体物理研究所,安徽 合肥 230009)
0 引 言
中国聚变工程实验堆(Chinese Fusion Engineering Testing Reactor,缩写CFETR)是中国自主设计和研制并联国际合作的重大科学工程[1]。CFETR内部属于极端环境,具有强辐射、高温、强磁场以及高真空等特点。此外,真空室内部设备众多,各种管道错综复杂,工作空间狭小,再加上舱内的某些部件会受到放射性和有毒物质的污染,即使在维护期间维护人员也不能直接对相关部件进行操作,需要借助于遥操纵手段在舱外通过机器人完成相应的操作。
由于维护空间较大,总设计总臂长较长;但受内壁腔体尺寸限制,单关节过长,自由度小的机械臂设计无法满足几何限制,故需要设计具有多个长度适合的关节以满足可达空间的需求[2]。结合以上设计要求,设计了一种基于底盘的9自由度冗余机械臂CMOR(CFETR Multipurpose Overload Robot)。该机械臂末端负载2.5 t、悬臂9 m、末端定位精度±10 mm,搭载着末端执行其并结合遥操作工具完成偏滤器第一壁的搬运、真空室清理以及管路维护等操作,如图1所示。
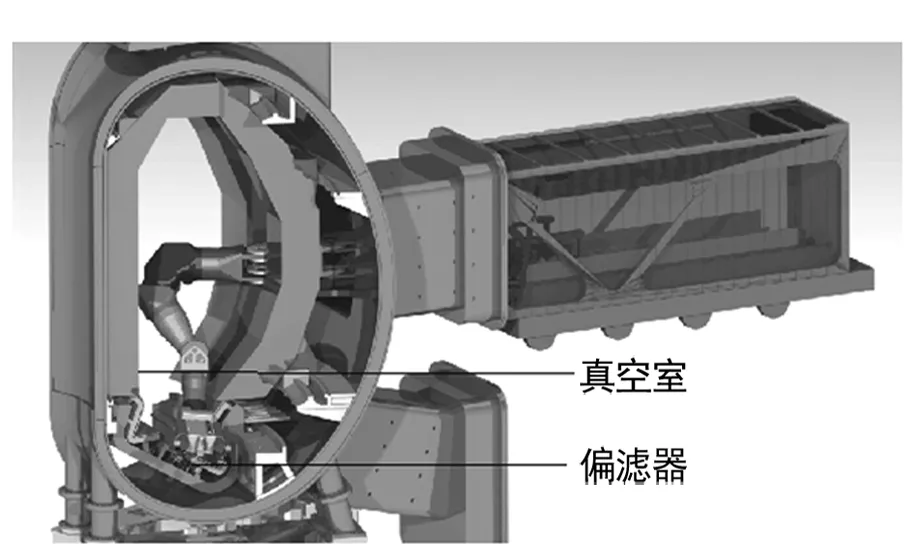
图1 CMOR系统在CFETR真空室内部图
CMOR机械臂共有8个关节,关节与关节之间按照要求有不同形式的关节驱动(见图2)。其中关节2、3为水平方向的偏航运动,关节4、6、8为轴线的旋转运动,关节5、7、9为竖直方向的俯仰运动。它主要用于真空室内部的维护工作,并通过底部轨道从中窗口送入真空室内部。中窗口为矩形截面,高为2 740 mm,宽为2 330 mm。真空室内部的维护空间是由高场侧包层、低场侧包层以及偏滤器表面组成的环形空间内。重载机械臂进入中窗口预设位置后,可通过底部轨道与真空室固定,机械臂本体可以用真空室内部空间实现从折叠状态到工作状态。CMOR机械臂在不同工作空间内所需达到的真空室扇区范围也不相同,分别为:在真空室包层及偏滤器轮廓组成的空间内需要能够达到±45°,在真空室内表面的空间内需要能够达到±11.25°。
1 CMOR机械臂运动学分析
1.1 正运动学求解
CMOR机械臂是一个九自由度机器人,包含一个移动关节和8个转动关节,负责将前端执行机器人送到接近维护点的位置。考虑机械臂的复杂程度和顺序结构,采用D-H法[3]建立九自由度机械臂各关节,及末端坐标系,如图3为机械臂的数学模型。根据该模型,可得到表1所列的机械臂各连杆的D-H参数。

图3 CMOR机械臂的DH模型
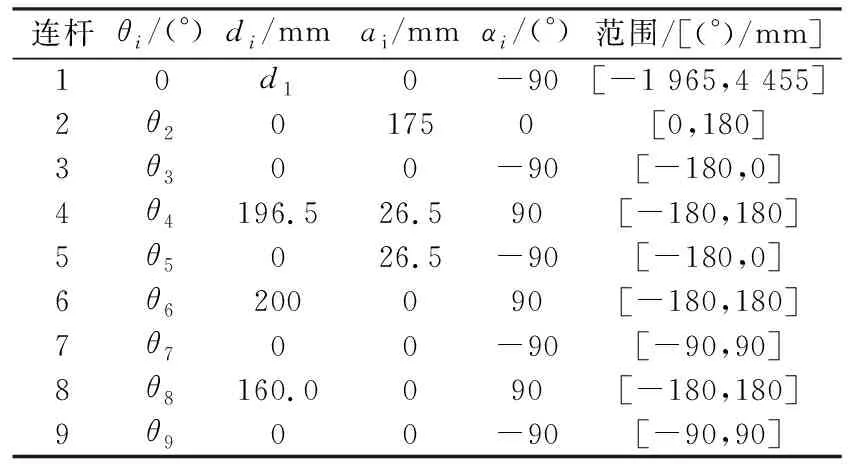
表1 CMOR机械臂模型的D-H参数表
根据空间坐标变化公式可得相邻两坐标系之间关系:
将连杆参数一次带入式子中,就可以得到机器人的其次变换矩阵:
机械臂的末端执行器的坐标系相对于基座标系的位姿变换矩阵可表示为:
对上式求解可得(仅展示末端位置P(px,py,pz)):
px=a2c2-d4(c2s3+c3s2)-d6(c5(c2s3+c3s2)+c4s5(c2c3-s2s3))-d8(c7(c5(c2s3+c3s2)+c4s5(c2c3-s2s3))-s7(c6(s5(c2s3+c3s2) -c4c5(c2c3-s2s3))+s4s6(c2c3-s2s3)))+a4c4(c2c3-s2s3)
py=a2s2+d4(c2c3-s2s3)+d6(c5(c2c3-s2s3)-c4s5(c2s3+c3s2))+d8(c7(c5(c2c3-s2s3)-c4s5(c2s3+c3s2))-s7(c6(s5(c2c3-s2s3)+c4c5(c2s3+c3s2))-s4s6(c2s3+c3s2)))+a4c4(c2s3+c3s2)
pz=d1-a4s4+d8(s7(c4s6+c5c6s4)+c7s4s5)+d6s4s5
1.2 逆运动学求解
CMOR机械臂是一个构型稍复杂的多自由度机械臂,其无法通过解析解或封闭解方法进行求解,需要利用数值法求解[4-6];文中使用基于雅可比逆矩阵的求解方法,其基本原理是给定机械臂末端的位姿,选取一组尽量合适的关节值为初始值,运用正运动学计算当前位置,当与目标位姿有误差时,采用雅可比伪逆来确定迭代方向,并通过迭代的方法使关节值收敛至目标位置。其算法如下:
(1) 已知机械臂末端目标位姿(Rref,Pref);
(2) 选择一组尽量接近目标的关节值q=(d1,θ2,θ3,θ4,θ5,θ6,θ6,θ7,θ8,θ9),由正运动学求出当前位姿(R,P);
(3) 计算位姿误差ΔP=Pref-P,ΔR=RTRref;
(4) 若误差小于预设误差阈值时,则当前q值为机械臂解;
(5) 若误差小大于预设误差阈值时,求解关节角度修正量dq,使q=q+dq,返回(2)。
关节速度和末端位置速度的线性关系:
dx=J·dq⟹dq=J+·dx
式中:J表示雅可比矩阵,但对于7自由度机械臂而言,由于其雅可比矩阵是个长方形,无法计算它的逆,用其伪逆J+代替(J+∈R6×9,J+=JT(JJT)-1),由上式得到dq=J+·dx,即为关节角度修正量。
1.3 CMOR机械臂运动学验证
首先,在MATLAB Robotics toolbox工具箱中通过编写程序输入机械臂参数建立一个CMOR机械臂模型。定义一组关节值A=[5.000,1.571,1.571,1.047,0.524,1.047,0.524,1.047,0.524],带入式(1)中可得:

使用函数fkine(A)同样可得到位姿:
比较可得T=Ta,验证了正运动学模型的正确性。以T作为已知位姿,通过逆运动学求解可得到一组关节值B=[-0.003,1.532,1.433,0.152 5,0.268,-0.883,-0.701,-2.467,0.281],将B带入正运动学方程可得:
比较可得Ta=Tb,验证了逆运动学求解方法的正确性。
2 工作空间求解
机械臂的工作空间是指在机械臂正常运行时,末端执行器的坐标原点能在空间活动的最大范围,或者说该原点所有可达点的体积空间,这一空间又称为可达空间或总工作空间。文中采用蒙特卡罗法求解机械臂的工作空间[7-8],求解步骤如下:
(1) 根据求解的正运动学可得到末端执行器原点在基座标系下的坐标P(px,py,pz)。
(2) 根据各个关节角度的转动范围,在Matlab中调用随机函数rand()生成每个关节变量的随机角度,跟据式(1)求出关节i的随机角度值:
θi=θi,min+(θi,max-θi,min)·rand(N,1)
(1)
式中:θi表示第i各关节转动角的最小值;θi,max-θi,min表示第i各关节转角的范围值;N为生成随机点的数量,N=10 000。
(3) 将产生的各关节随机角度值带入坐标(px,py,pz)中,可以得到机械臂的工作空间。使用的随机点的数量越多,则生成的工作空间与实际的操作空间越接近。
用Matlab生成的CMOR机械臂工作空间如图3所示。
从图3可以得出用蒙特卡罗法得到的CMOR机械臂末端的活动空间,范围是沿X(-800 0,800 0),Y(-420 0,440 0),Z(-600 0,800 0)三个坐标方向围成的一个椭圆体的区域。结合真空室的尺寸很容易看到,在xoz和yoz平面的末端点能够覆盖整个工作环境,由图5可得再xoy平面可得CMOR的末端可满足达到真空室内±45°的扇形范围。
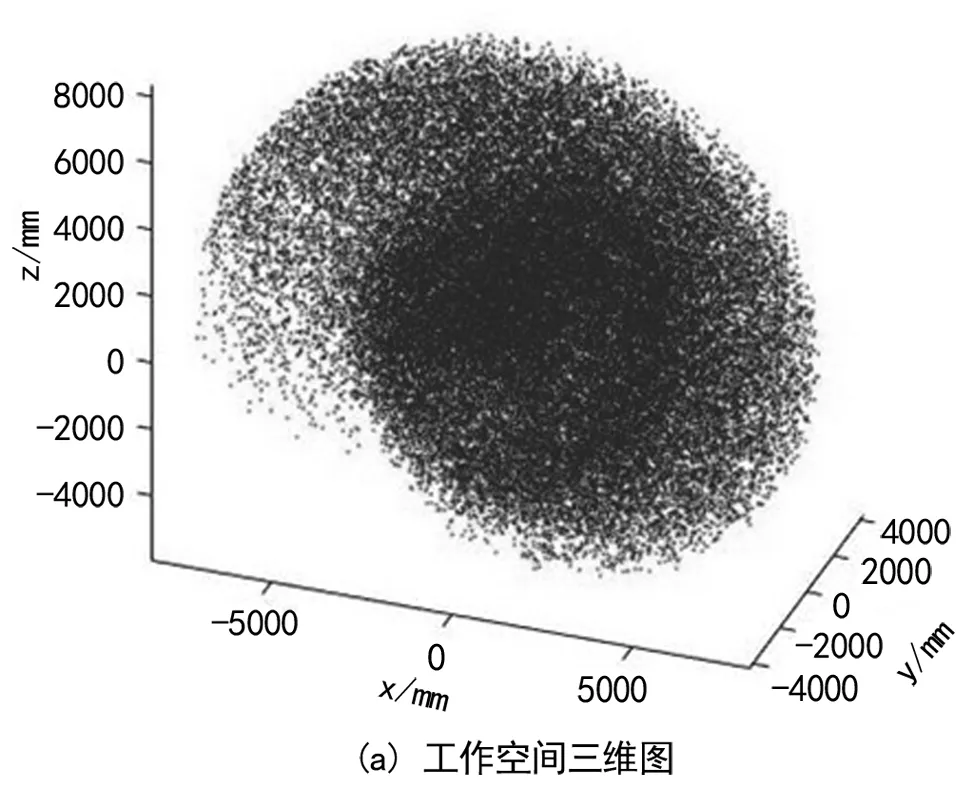
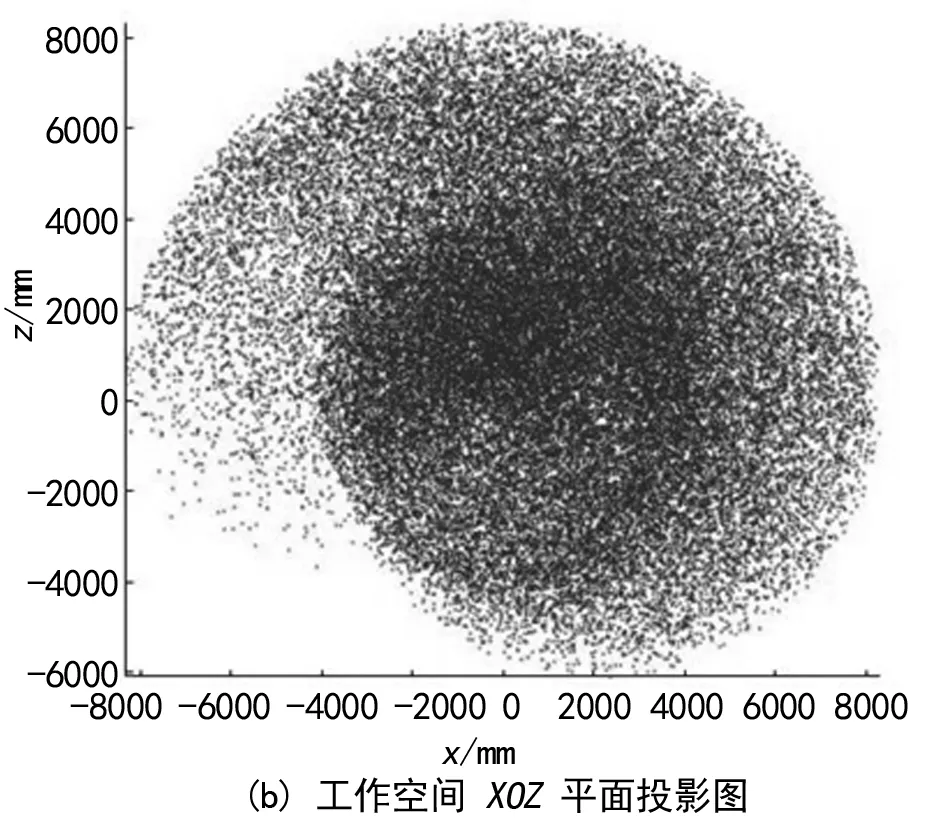

图4 冗余重载机械臂的工作空间
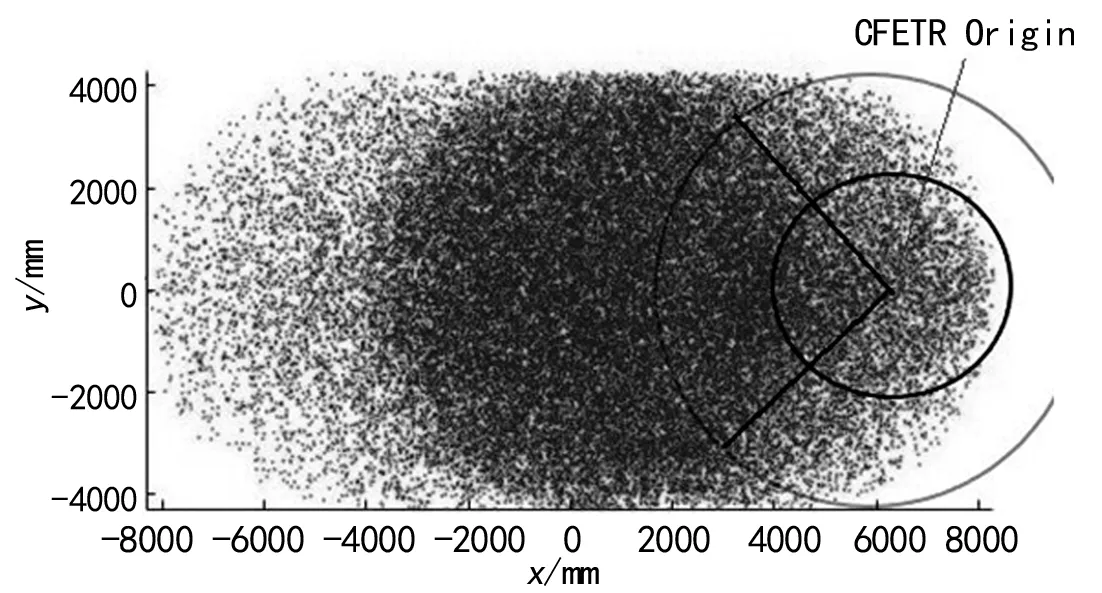
图5 CFETER与冗余机械臂工作空间分析图
3 轨迹规划
3.1 五次多项式轨迹规划
机械臂的轨迹规划分为笛卡尔空间和关节空间。在关节空间内进行轨迹规划有以下优点:在线计算量小,即无需进行机械臂的逆解或正解解算、不受关节奇异构型影响。但前期对应的操作空间的轨迹无法预测,增加了机械臂与环境碰撞的可能[9]。采用五次多项式曲线插值算法[10]进行CMOR机械臂的轨迹规划。以关节角度、角速度以及角加速度作为边界条件,以确保各关节变量的连续无突变。公式如下:
θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
同时我们要限制路径起始点和终止点的关节角度、角速度、角加速度:
由上式可知,该方程组由6个方程和6个未知数。求解方程可得:
将系数带入轨迹方程中,可以得到机械臂的五次多项式插值曲线的轨迹方程。
3.2 轨迹规划的仿真
为近一步验证建立的运动学方程的准确性还需进一步的在虚拟样机进行验证。
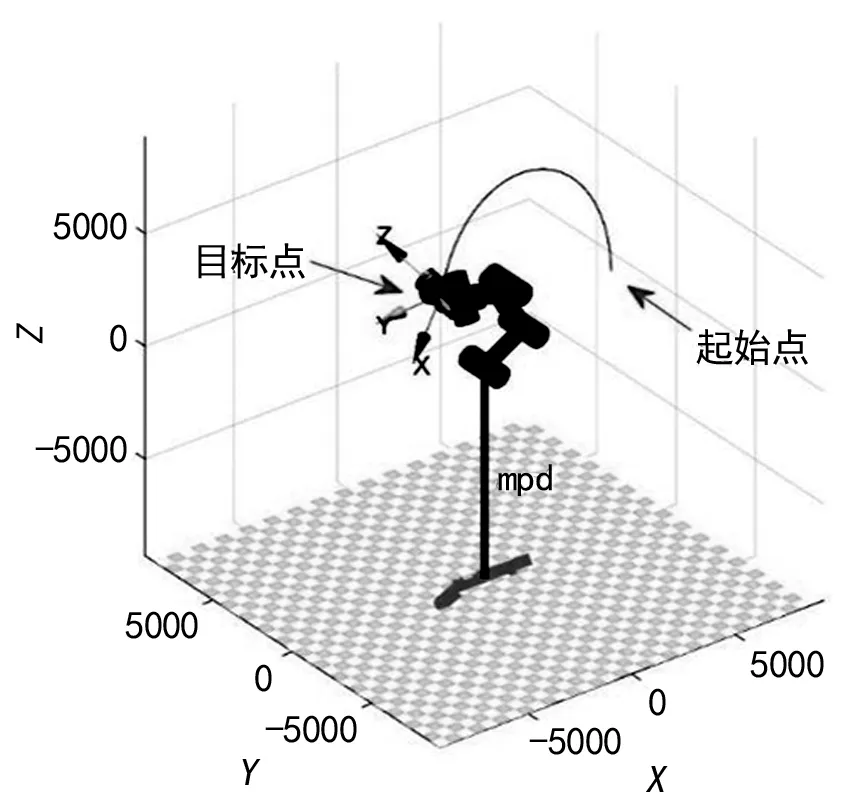
图6 CMOR机械臂的运动轨迹图
首先,在Matlab中设定好机械臂末端位置的初始位姿A和需要移动的到的目标位姿B,采用五次多项式插值算法完成轨迹规划。在Matlab中编写程序模拟仿真过程,设置步长为40,生成机械臂末端位置在在空间中的运动曲线。仿真结束后生成机械臂的9个关节位置、速度、加速度随时间变化曲线图。分析图像可以得到机械臂从初始位置到目标位置的整个运动过程平滑无突变。

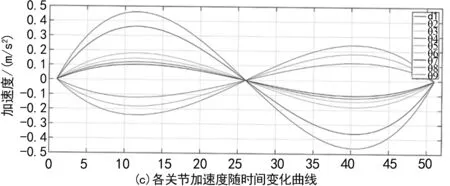
图7 各关节参数变化曲线图
各关节运动参数随时间变换曲线如图5所示,从上到下分别为关节1、关节4、关节6、关节3、关节8、关节9、关节7、关节5和关节2,9条关节都相对平滑无冲击,并未出然增加或减少的突变现象,能完成点到点的高速运动,证明了机械臂结构的正确性以及运动学方程的正确性。
4 结 语
以设计的9自由度CMOR机械臂为研究对象,采用D-H参数法、雅可比伪逆法建立了CMOR机械臂的运动学模型,基于Matlab建立了机械人系统的仿真模型,采用蒙特卡罗法计算了机械臂的工作空间。同时开展了关节空间机械臂轨迹规划的研究,研究了五次多项式插值法点到点轨迹规划,并机型仿真验证,仿真结果表明建立的机械臂模型和运动学方程的正确性,为该机械臂的后续工作提供了理论依据。

