舰船平台设备的减振设计及振动性能研究
王云鹏, 申 伟, 张 华, 徐 聪
(中车青岛四方车辆研究所有限公司,山东 青岛 266031)
0 引 言
随着远洋运输和海洋军事的蓬勃发展,作为运用介质的舰船所面临的运用环境更加错综复杂。高速舰船在航行过程中,可能遭遇强风、大浪等各种突发状况,从而引起船体剧烈振动,影响仪器设备的正常工作,降低使用精度,缩短使用寿命,严重时会导致设备出现倾覆、损坏等安全性问题。因此在舰船的设计过程中,仪器设备的减振设计是重要保障措施之一。
减振器是用来衰减舰船设备振动和冲击干扰的有效元件,如何设计或选择减振器的性能参数,如何进行合理的减振系统布置对发挥减振器的作用至关重要。目前舰船上使用的减振器型式多种多样[1-2],以被动式减振器居多,一般设计为单层或双层减振器系统,其特点是简单有效,同时使用及维护方便。随着对舰船设备振动性能的要求越来越高,减振性能更加优异的主被动复合型减振器[3]、主动智能型减振器[4]也越来越多得到应用。
笔者以某舰船所载平台设备为例,根据其振动性能设计要求,通过理论计算和仿真模拟分析,设计该平台设备的减振系统,并对设备进行振动台试验验证特性分析,以达到减少平台设备振动和保证系统稳定的目的。
1 系统结构及设计要求
平台设备系统安装在舰船甲板的集装箱式方舱内,为双层结构,采用板材焊接而成。方舱固定安装在舰船的甲板上,直接承受来自舰船的环境载荷和自然环境载荷的作用,同时将激励载荷传递到平台设备上。平台减振系统的设计目的是隔离或抑制舰船激扰载荷对平台的干扰,保护平台上设备的安全,提高设备的环境适应能力。平台设备系统的结构组成及安装位置如图1所示。

图1 平台设备组成及安装布局
该平台系统的减振设计要求如下。
(1) 平台系统的一阶固有频率不大于8 Hz。
(2) 从12 Hz开始,激励振动开始衰减。
(3) 在30 Hz时,振动衰减不低于20 dB。
(4) 减振系统的共振放大倍数不大于5。
2 系统减振性能计算
2.1 减振系统设计
根据平台系统的结构特点和减振设计要求,可以将方舱与舰船甲板看做一体,从而将系统简化成单自由度的弹簧-阻尼-质量系统[5],如图2所示。

图2 平台系统力学模型
根据振动力学理论,系统的运动方程为:
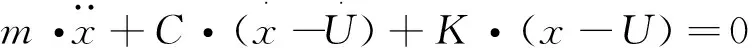
式中:m为平台系统的质量,kg;K为平台减振系统的刚度,N/m;C为平台减振系统的阻尼,Ns/m。

已知平台系统的总质量m=12.5 t,一阶固有频率要求不大于8 Hz,则由ωn得到k=(2πf)2m,即可求出平台系统在工作状态时,满足系统一阶固有频率要求的隔振器的动刚度(垂直方向)为:
k动≤31.5 kN/mm
当取隔振器(橡胶类)动静刚度比d=1.3时:
k静=k动/1.3≤24.23 kN/mm。
同时还要对减振系统的静态变形量进行校核,以满足设备安装和使用的间隙要求。水平方向的减振器刚度设计方法类同,不再详述。
以垂向减振为例给出了该平台系统的垂向隔振率。从图3中看出,当空气弹簧的阻尼比δ=0.105时,在30 Hz的振动衰减率为R=97.2%,满足衰减至少20dB的设计要求(即隔振率至90%),同时系统的共振放大倍数小于5,说明平台系统的减振性能满足设计要求。

图3 平台系统的垂向隔振率
由于平台的尺寸大,考虑到系统的稳定性,初步设计10套减振器[7],在平台系统的纵向两侧分别布置5套。综合上述计算结果,设计具有较低自振频率的空气弹簧减振器[8],该型减振器的横向刚度与垂向刚度接近,可以提高平台横向稳定性,每组空簧间相互串联,由一套高度阀控制,使平台能够保持一定高度,其结构如图4所示。该型空气弹簧在额定载荷下的垂向刚度为590 N/mm,水平刚度为480 N/mm。此时平台减振系统的一阶垂向固有频率为fV=3.43 Hz,一阶水平固有频率为fL=3.09 Hz,满足平台减振系统一阶固有频率小于8 Hz的设计要求。

图4 平台减振系统用空气弹簧结构
平台系统的质心存在一定偏移,根据重心和支撑点力矩平衡原理,设计空气弹簧的安装位置。由于空气弹簧沿平台系统的纵向每侧分别布置5套,即存在5个支撑点,属于超静定问题,因此空气弹簧的布置位置有不唯一解,按照计算结果并同时根据平台实际空间限制,取其中一解为空气弹簧的布置位置,如图5所示。布置方案首先保证工作状态下,平台系统的安全与稳定,经计算校核,该布置方案满足稳定性要求。为了防止平台系统内部设备在倾斜或摇摆工况下与方舱箱体发生碰撞或接触,在空气弹簧内部还设计了垂直方向和水平方向的弹性止挡结构。

图5 平台系统一侧的空气弹簧布置位置
2.2 减振系统振动传递校核
在平台减振系统的基本减振性能指标满足设计要求后,按照GJB150.16A-2009《军用装备实验室环境试验方法 第16部分:振动试验》中7.3.1的方法分别对减振系统水平放置、倾斜20°两种工况在舰船随机激励载荷下的振动情况进行计算校核。
由于平台系统的尺寸、质量较大,后期试验验证存在一定困难,因此在进行减振试验的计算校核时将平台减振系统的质量、尺寸等比例缩小至原始参数的0.4倍,同时将空气弹簧的数量减为4个,空气弹簧的刚度保持不变,即对平台系统的缩比模型试验工况进行了计算验证[9]。
平台系统结构紧凑,质量大,各设备几乎无变形,因此不考虑系统部件的弹性变形,利用广义拉格朗日法建立平台减振系统的多刚体分析模型。在考虑系统阻尼的情况下,平台减振系统为非保守系统,系统中存在着由阻尼产生的非势能力,假定阻尼是广义速度的函数,其拉格朗日方程为[10]:
式中:T为平台系统振动时的动能;q为系统的广义坐标列阵;Q为广义力列阵;ρ为对应完整约束的子列阵;μ为对应非完整约束的拉氏乘子列阵。
表1给出了30 Hz时平台减振系统在三种工况下振动衰减率的线性分析结果,结果显示平台无论是水平放置还是倾斜20°,减振系统在三个方向的振动衰减率均大于30dB,满足大于20dB的设计要求。从图6所示结果来看,平台减振系统在水平放置、倾斜20°及缩比模型倾斜20°时的加速度功率谱密度规律是基本相同的。与原始尺寸模型相比,缩比模型在5 Hz以下的低频区域略有不同,这是由于缩比模型与原始模型的支撑工装结构不同导致。

表1 平台系统振动衰减率计算结果

图6 各工况下平台系统的垂向振动响应
3 系统振动试验及分析
平台减振系统按照GJB150.16A-2009的方法进行试验,单独对系统进行三个方向的舰船随机振动试验[11],验证平台减振系统在倾斜20°时的减振性能。如前所述,平台减振系统试验时采用缩比实物模型,模型中各结构件利用螺栓或焊接刚性连接,通过空气弹簧将试验模型与倾斜工装连接在一起,再将工装利用螺栓固结在振动台水平滑台上。试验采用两点平均控制方式,两个控制点均位于试验件与工装的连接面附近以保证激励信号的准确[12],平台系统布置上、下两个测点(即顶部测点和空簧上部测点)。试验现场如图7所示。

图7 试验现场图
在舰船随机振动试验过程中和试验结束后,平台减振系统未发生倾覆,系统稳定性良好。表2中试验结果显示,在30 Hz时,平台系统在三个方向随机激励下的振动衰减率均大于20 dB,符合设计要求。

表2 平台系统的振动衰减率振动试验结果(空簧上部测点)
从图8看出,平台减振系统缩比模型的上、下两个测点均具有较好的减振性能,在10 Hz以下频率范围内,上、下测点的加速度功率谱密度比较接近,随着激励频率的提高,两个测点的加速度谱密度曲线出现一定分离,这是由于下部测点距离减振器较近,减振系统较好发挥了隔振作用,而上部测点距离激励面位置较远,是结构自身响应放大导致。

图8 平台系统缩比模型振动试验的垂向振动响应
表1、2两种分析结果显示平台减振系统的振动衰减率数值差距较大,同时图6的仿真结果与图8的试验结果虽然规律类似,但在局部表现上有所差异。经分析,主要原因是平台系统试验时在30Hz以上激励出现了二阶系统共振,导致系统的减振效率下降。
系统试验出现二阶共振有以下两种可能性:
(1) 工装或平台在该频内上有固定的模态。对工装和平台系统建立有限元模型进行模态分析,分析结果显示工装和平台系统在该频段内均没有固定模态,可以排除该因素。
(2) 试验时空气弹簧中的弹性止挡发生接触,导致支撑刚度急剧变大以致系统的固有频率发生改变。通过对空气弹簧弹性止挡进行不同压缩量的刚度测试,发现当止挡压缩到一定程度时,其刚度对应的系统频率正处于该频率范围,认定是该原因导致平台减振系统出现了二阶共振。可在后续设计中通过调整空气弹簧内部间隙或施加主动控制单元适时调整刚度来解决该问题。
对平台系统进行的振动仿真分析是基于线性系统原则,没有考虑系统支撑及结构中出现的非线性因素,计算结果会偏于乐观,这也是导致计算与试验数据存在差异的原因之一。
4 结 论
作为舰船甲板上的重要设备,平台系统的振动性能是保证其正常工作的关键。通过对平台系统进行减振设计、校核及振动试验分析,总结如下。
(1) 良好的弹性减振设计可以明显衰减设备的振动,此文所设计的空气弹簧减振系统在常用工况下能够较好的实现平台系统减振功能。
(2) 此文计算基于线性化分析,导致在减振设计分析时无法考虑系统的非线性特性,难以模拟振动试验过程中出现的极端状况,与试验结果存在一定差异。
(3) 对于舰船重要设备,文中设计的被动式减振系统在面对极端恶劣工况时减振性能略显不足,后期可适当采用主动控制措施进行进一步优化。

