调平误差对装填力的影响分析及仿真
徐如强, 杨垂锦, 赵国建, 丁 宇
(1.北京机械设备研究所,北京 100854; 2.贵州航天乌江机电设备有限公司,贵州 遵义 563003)
0 引 言
导弹装填装置是技术阵地内的重要支援设备之一,是用于将导弹装入或退出贮运箱(筒)的重要设备。在导弹的装填过程中需要保证贮运箱内导轨与装填装置导轨平齐及水平,然后导弹在推弹装置作用下沿导轨滑动直至装填到位。在调整装填装置导轨与贮运箱导轨平齐及水平的过程中通常使用水平仪和水准仪进行调平。在此过程中,除设备生产装配产生的误差外还有测量仪器误差、观测误差、外界条件影响产生的各种误差[1],调平误差的存在必然导致装填设备导轨与贮运箱导轨难以对齐及水平,特别是在长度方向通常难以调整水平,将对装填力产生影响甚至造成装填过程中导弹的损坏,而过高的调平精度将对设计和使用造成不利的影响。因此有必要对调平误差与装填力的影响关系进行分析研究,有助于为设计和使用过程提供合理的调平误差限值。
笔者通过对导弹装填设备装填过程的逐步分析,推导出了装填过程中装填力与调平误差间的关系方程。同时采用MSC/Adams动力学仿真软件对装填过程进行仿真分析,得出某装填装置在调平误差下的装填力变化曲线,可较简便的分析出装填力的变化是否满足设计和使用要求,同时达到验证该调平误差是否满足设计和使用要求的目的。
1 装填过程
理想调平状态下,装填装置与贮运筒的导轨完全齐平,导弹沿导轨直接滑入贮运筒,装填过程示意简图见图1所示。

图1 装填过程示意简图
因调平误差的存在,无论装填装置或贮运箱均可能与水平方向存在倾角,如此则共有多种调平工况,考虑工况分析复杂程度,本文仅对其中一种调平工况即装填装置下倾、贮运箱上倾工况进行全装填过程装填力的分析,见图2~4。

图2 导弹在装填装置上滑动示意图
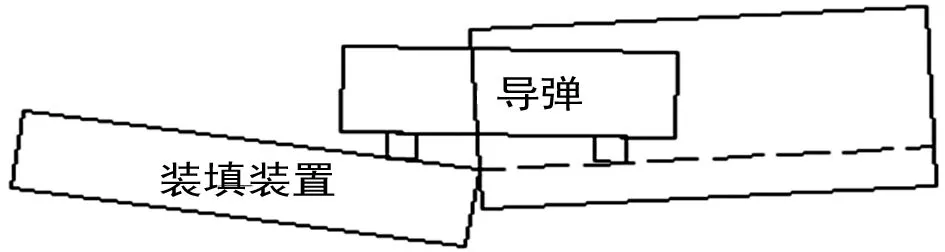
图3 导弹同时在装填装置及贮运箱上滑动示意图
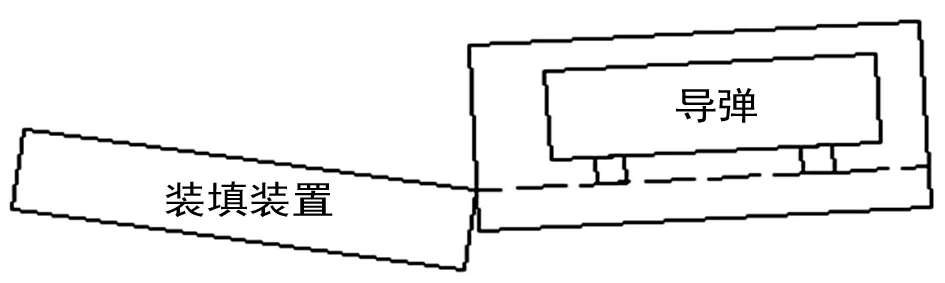
图4 导弹在贮运箱内滑动示意图
2 装填力分析
装填装置采用链传动形式驱动导弹滑动,在分析过程中不考虑链传动多边形效应及各种附加载荷对导弹运动速度变化的影响,将推弹装置及其与导弹的作用点的运动看作匀速运动。则上述装填工况的分析如下文所述。
2.1 在装填装置导轨上滑动
导弹完全在装填装置导轨上滑动时,其力学分析见图5。
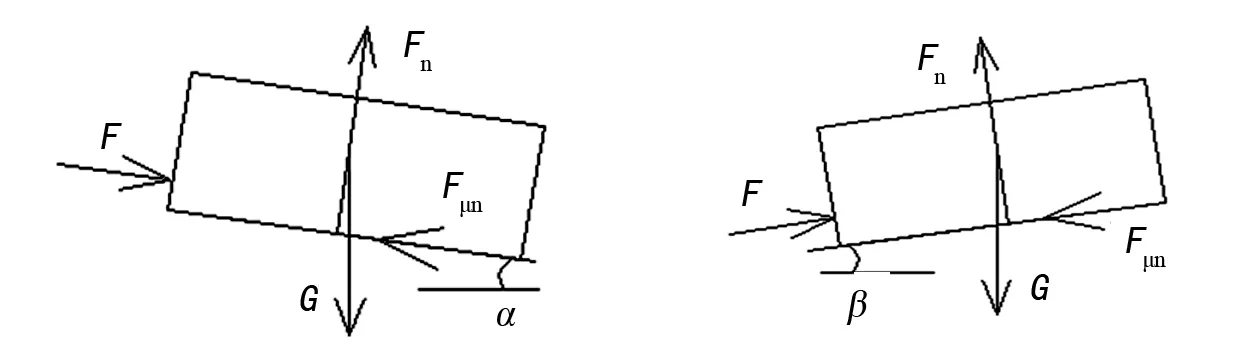
图5 在装填装置上滑动时的 图6 在贮运箱滑动时的 力学分析 力学分析
依据受力平衡关系可得:
F+G×sinα=μ×Fn
(1)
G×cosα=Fn
(2)
由式(1)、(2)可得导弹完全在装填装置导轨上滑动时的装填力为:
F=μ×G×cosα-G×sinα
(3)
式中:F为装填装置对导弹的装填力;G为导弹自重;Fn为导轨对导弹的支撑力;Fμn为导轨对导弹的摩擦力;μ为导轨与导弹间的摩擦系数;α为装填装置倾角或调平误差。
2.2 在贮运箱导轨上滑动
导弹完全在贮运箱导轨上滑动时,其力学分析见图6。
依据受力平衡可得
F=G×sinβ+μ×Fn
(4)
G×cosβ=Fn
(5)
由式(4)、(5)可得导弹完全在贮运箱导轨上滑动时的装填力为:
F=μ×G×cosβ+G×sinβ
(6)
式中:F为装填装置对导弹的装填力;G为导弹自重;Fn为导轨对导弹的支撑力;Fμn为导轨对导弹的摩擦力;μ为导轨与导弹间的摩擦系数;β为贮运箱倾角或调平误差。
2.3 在不同导轨上滑动
当导弹前后支脚分别在装填装置及贮运箱导轨上滑动时(见图3),导弹作平面运动,其受力分析见图7,其中A点表示导弹后支脚,B点表示导弹前支脚,C点表示导弹质心点,O点表示装填装置导轨与贮运箱导轨对接点,D点为运动瞬心。
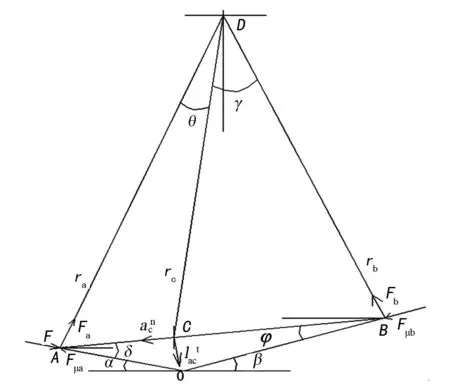
图7 在不同导轨上滑动时的力学分析
依据理论力学[2]中运动学、动力学及几何关系可得:
(7)
(8)
(9)
(10)
La=va×t
(11)
Lb=vb×t
(12)
(13)
(14)
θ+γ=α+β
(15)
(16)
(17)
F×cosα+Fa×sinα-Fμa×cosα-Fb×
sinβ-Fμb×cosβ=m×acx
(18)
-F×sinα+Fa×cosα+Fμa×sinα+Fb×
cosβ-Fμb×sinβ-G=m×acy
(19)
Fμa=μ×Fa
(20)
Fμb=μ×Fb
(21)
(22)
(23)
[(F-Fμa)×sinδ-Fa×cosδ]×L1+[Fb×
(24)
α+β=φ+δ
(25)
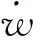
式(7)~(25)共有19个方程,29个参数,其中可作为已知量的参数有va、m、G、L、L1、μ、Jc共7个,则在理论上可求解出装填力F关于α、β、t的表达式:
F=F(α、β、t)
(26)
由上述式(3)、(6)及式(26)即可确定在导弹装填过程中装填力与调平误差的关系,但因式(26)在实际求解过程中较为困难,可采用数值计算的方式进行,在此不再进行求解。
3 装填过程仿真
MSC/Adams软件以计算多体动学为理论基础,研究复杂系统的运动学和动力学关系,结合高性能计算机来对产品进行仿真计算,进而得到各种性能数据,帮助设计者发现问题并解决问题[3]。本文通过creo2.0软件建立了某型装填装置装填过程的简化仿真模型,通过MSC/ADAMS软件进行装填过程的动力学仿真分析,得到装填过程中装填力的变化曲线。
某型号导弹装填过程的简化仿真模型如图8所示,导弹质量按1 000 kg计,支脚间距缩比为1 000 mm,与导轨动摩擦系数按0.1,当调平误差α=0.5°,β=1°时的仿真结果见图9。图中粉线表示装填过程中的推弹架对导弹的作用力即推弹力的变化曲线,蓝线表示贮运筒与导弹间的摩擦力分量变化曲线,红线表示装填架与导弹间的摩擦力分量变化曲线。

图8 仿真简化模型
从图9中可以看出:0~5 s间,导弹在装填架上移动;5~55 s间,导弹前支脚作用在贮运筒导轨上,后支脚作用在装填架导轨上;55~60 s,导弹完全滑上贮运筒导轨。在5~55 s的装填过程中,装填力曲线总体上较为平整,相较理论分析而言更直观简洁,同时可以得出理论分析的过程较为复杂,可以进一步进行简化。通过仿真曲线可直观的看出该调平误差设定下的装填力变化情况,进而为装填装置调平误差的限值确定提供依据。

图9 装填力仿真曲线
4 结 语
通过理论分析研究,推导出了一种工况下装填力与调平误差间的全装填过程的数学关系。通过MSC/Adams软件进行动力学仿真,得出某调平误差工况下全装填过程的装填力曲线。通过曲线变化情况得出需要对导弹在不同导轨上滑动时的理论分析过程进行进一步的简化,以便更好的指导设计和使用工作。理论分析及动力学仿真均可为装填装置设计及使用过程中调平误差的限值确定提供一定的理论依据。

