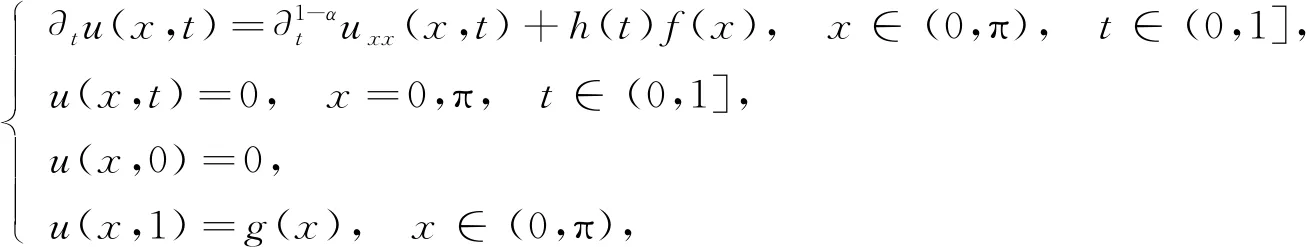带有Riemann-Liouville导数的分数阶热传导方程逆源问题的正则化方法
史暖峰, 冯立新
(1. 黑龙江大学 数学科学学院, 哈尔滨 150080;2. 利沃夫国立理工大学 应用数学与基础科学学院, 乌克兰 利沃夫 79013)
0 引 言
热传导方程逆源问题是一类重要的热传导反问题, 目前已得到广泛关注. 文献[1]把热能量作为测量数据重构仅依赖于时间的逆源问题, 数值上采用边界元法与二阶Tikhonov正则化法, 通过广义Fourier方法证明了反问题解的存在性、 唯一性以及对测量数据的连续依赖性; 文献[2]把若干空间上的积分作为测量数据重构二维热传导方程的热源项, 数值上采用共轭梯度法对该问题进行求解; 文献[3]根据初始数据和边界数据及两个附加数据重构热传导方程中的两个可分离源项, 并提出了一种连续逼近的数值迭代算法; 文献[4]把仅依赖于时间的逆源问题转化为第一类Volterra积分方程, 用Tikhonov正则化方法求解了该问题; 文献[5]基于分离变量法, 利用Tikhonov正则化方法, 重建时间分数阶热传导方程热源项, 并分析了正则解的收敛性; 文献[6]研究了带有Caputo导数的一阶时间分数阶热传导方程反问题, 并基于特征函数展开, 利用解析延拓反演源项证明了时间分数阶只与空间变量有关的源项反问题的唯一性; 文献[7]基于叠加原理, 提出了一种改进的拟边界值方法解决时间分数扩散方程的逆源问题; 文献[8]利用Landerweb迭代正则化方法解决时间分数阶扩散方程逆源问题, 并给出了先验和后验两种选取策略下正则解和精确解的误差估计; 文献[9]采用分数阶Landerweb方法反演了未知空间源项, 该方法优于传统Landerweb方法, 计算速度较快; 文献[10]研究了多项时间分数阶扩散方程, 根据Laplace变换证明了解的衰减率由时间分数导数的最小阶数给出; 文献[11]研究了带有Riemann-Liouville导数的热扩散方程反问题, 利用准边界值法克服问题的不适定性, 给出了先验参数选取时正则解和精确解的误差估计. 目前, 对带有Caputo导数的分数阶热传导逆源问题已有许多研究成果, 但对于带有Riemann-Liouville导数的分数阶热传导方程逆源问题的研究文献报道较少. 本文主要讨论带有Riemann-Liouville导数的分数阶热传导方程逆源问题, 利用分离变量和Laplace变换构造Tikhonov正则化近似解, 并证明正则解的收敛性.
1 问题描述
考虑如下分数阶导数热传导方程:

(1)
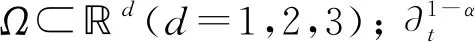
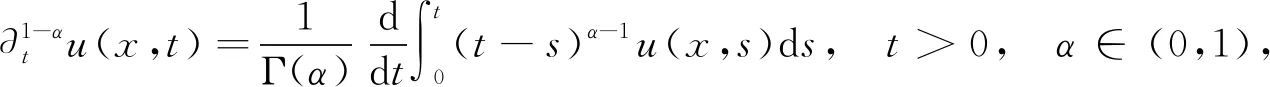
(2)
Γ(·)是Gamma函数;A是一个对称的椭圆算子[13], 定义为

(3)
逆源问题: 给定A,h(t), 根据末时刻T的观测数据gδ(x)重构未知源项f(x), 其中观测数据gδ(x)满足
‖gδ(x)-g(x)‖L2(Ω)≤δ,
(4)
这里δ为误差水平.
2 正则解的构造及误差估计
椭圆算子A在Ω上满足齐次Dirichlet边值条件的特征值与规范的特征向量(λp,φp(x)), 即
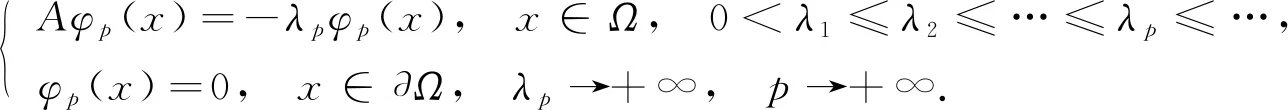
(5)
利用分离变量法假设精确解u(x,t)为

(6)
对方程(1)中t变量做Laplace变换, 有
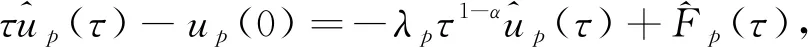
(7)

根据文献[12]可知,
(8)
其中Eα,β是Mittage-Leffler函数[14], 其定义为

利用u(x,0)=0和Fp(τ)=〈h(τ)f(x),φp(x)〉, 可得
(9)
从而可得
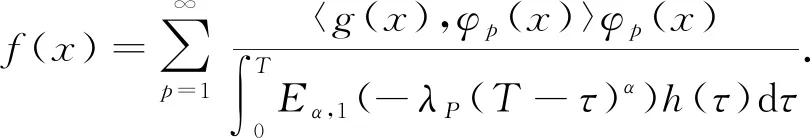
(10)

下面引进线性算子K:L2(Ω)→L2(Ω), 定义为
其中
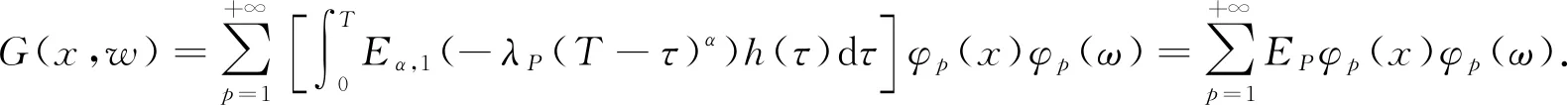
(12)
引理1[11]K是L2(Ω)→L2(Ω)上的自伴紧算子且为单射.
本文考虑的逆源问题可抽象地写为如下算子方程形式:
Kf(x)=g(x).
(13)

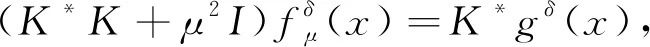
(14)
其中μ>0, 为正则化参数.由式(12),(14)计算得
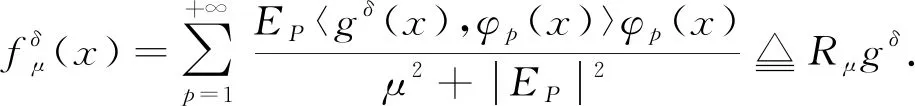
(15)
2.1 先验参数选取下正则解与精确解的误差估计
假设fμ(x)是如下方程的解:
K*Kfμ(x)+μ2fμ(x)=K*g(x).
(16)
由算子K的定义易知

(17)
由式(15),(17)得
即
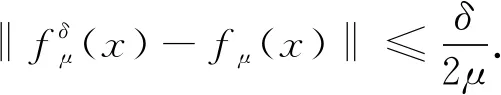
(18)
引理2设f(x)∈Hk(Ω),E为常数, 满足E≥‖f‖Hk(Ω), 则如下估计成立:

(19)

证明: 由式(10),(17)可得
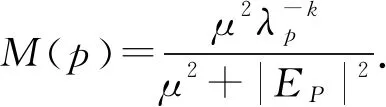

(20)
根据文献[11]知,
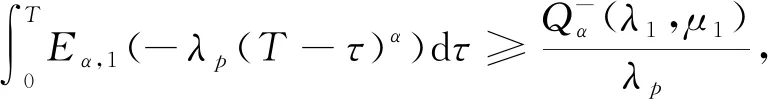
(21)


(22)
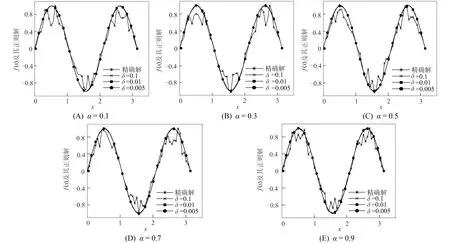
情形1) 当0 N1={p∈,, (23) 则有 选取m=1-k且‖f(x)‖Hk(Ω)≤E, 有 即 (24) (25) 从而式(19)成立, 证毕. 根据引理2, 式(26)有两种情形. 情形1) 当0 情形2) 当k≥1时, 有 (28) 由引理2和式(27),(28)可得如下定理. 基于Morozov相容性原理, 选取正则化参数, 即选择μ>0, 使得 (29) 直接计算可得 某公司6万t/a镍电解项目采用硫化镍电解精炼工艺,主要包括电解、三段净化、电溶造液3个子项,于2012年8月建成投产。在项目论证、设计、建设过程中,充分考虑了混酸体系含有介质腐蚀环境,结合防腐新技术的发展,对本项目防腐方法进行了优化改进。6万t/a镍电解项目整体工程质量优良,并获得了2012至2013年度中国建筑行业工程质量最高荣誉——鲁班奖。项目建成后经过5年多的生产运行跟踪,生产能力达到或超过设计指标,防腐效果基本达到了生产运行要求,保障了生产的顺利、稳定运行。 (30) 因此 即 从而 于是 (31) 证明: 因为 假设观测数据gδ(x)满足条件(4)和‖gδ(x)‖≥τδ, 则有 由式(14)知 再结合式(29)得 (32) 根据式(31),(32)可知选取后验参数时, 正则化参数选取范围为 (33) 由式(29),(33)可得如下定理. 定理2在后验参数选取准则(29)下, 正则化参数的选取范围为式(33). 所以 于是 (34) 因为K:L2(Ω)→L2(Ω)是有界线性算子, 对任意z∈L2(Ω), 有 (35) 所以 即 (36) 又因为K:L2(Ω)→L2(Ω)是单射算子, 所以Range(K*)在L2(Ω)中稠密, 由式(36)可知 由式(29),(36)可得如下定理. 为验证本文正则化方法的可行性, 下面给出求解分数阶导数逆源问题的实例.考虑边值问题: (37) 其中 方程(37)的精确解为 u(x,t)=t1+αsin(3x). 数值实验过程如下: 1) 对空间Ω进行等距剖分, 剖分节点为 2) 对g(x)加扰动可得观测数据gδ(x): eprand(·)=δ(2rand(·)-1),gδ(·)=g(·)(1+eprand(·)); 3) 为方便比较, 给出精确解和正则解的相对误差为 4) 根据文献[15]的算法计算Mittag-Leffler函数, 利用 可得 由式(15)得正则解为 表1列出了5种α取值下精确解和先验参数选取正则解的相对误差, 表2列出了5种α取值下精确解和后验参数选取正则解的相对误差, 其中α∈{0.1,0.3,0.5,0.7,0.9}.图1为先验参数选取时精确解和正则解的比较, 图2为后验参数选取时精确解和正则解的比较, 其中N=50,α∈{0.1,0.3,0.5,0.7,0.9}. 表1 先验参数选取精确解与正则解的相对误差 表2 后验参数选取精确解与正则解的相对误差 由表1、 表2及图1、 图2中反演结果可见, 当δ→0时, 误差减小, 正则解接近于精确解, 且后验参数选取策略结果优于先验参数选取策略, 表明本文的正则化方法有效. 图1 先验参数选取精确解与正则解的比较Fig.1 Comparison between exact solution and regularization solution for priori parameter choice rule 图2 后验参数选取精确解与正则解的比较Fig.2 Comparison between exact solution and regularization solution for posterior parameter choice rule 综上, 本文利用Tikhonov正则化方法, 讨论了带有Riemann-Liouville导数的分数阶热传导方程逆源问题, 给出了先验正则化参数选取时正则解的收敛速度估计及后验正则化参数选取时正则化参数的取值范围, 并证明了其正则解的弱收敛性. 数值实验结果表明该方法有效.
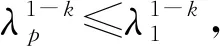
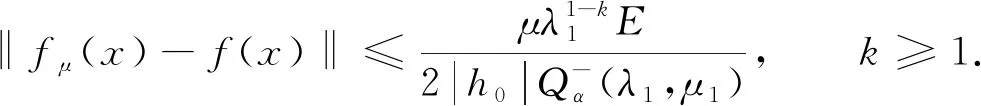

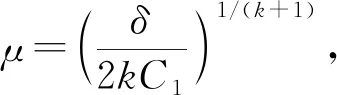
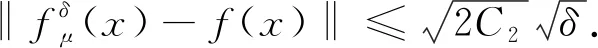

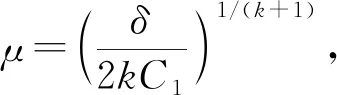
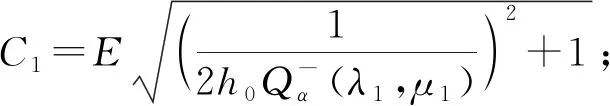
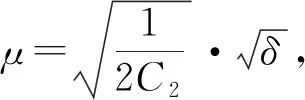

2.2 后验参数选取下正则解与精确解的误差估计

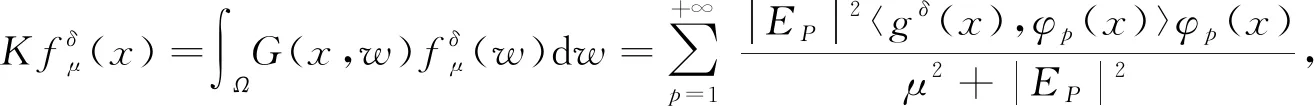
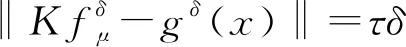

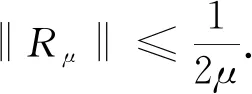


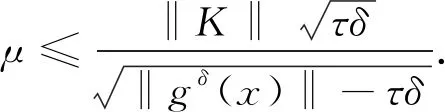

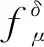
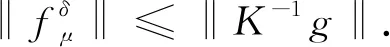
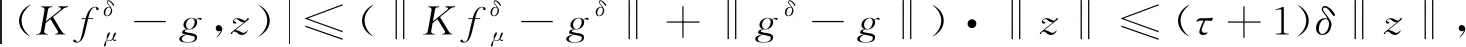
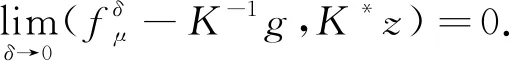
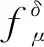
3 数值实验