基于曲率模态变化率的复合材料梁脱层损伤识别 ①

杜 宇，何梅洪，李菊峰

(1.天津市现代机电装备技术重点实验室, 天津 300387；2.天津工业大学 机械工程学院, 天津 300387)

0 引言

复合材料结构由于其比强度大和比刚度高等优势，广泛用于航空、航天等领域。但由于复合材料的各向异性特点，在服役使用过程中，容易发生脱层损伤，且损伤会降低结构的刚度和强度，给结构安全带来一定的隐患。因此，对复合材料脱层损伤检测具有重要的现实意义。

在复合材料损伤识别方面，无损检测技术发展尤为突出。如射线检测、声发射检测、涡流检测和超声检测等都被用于复合材料的无损检测[1-4]。由于结构的损伤会导致刚度的变化，进而引起结构模态(固有频率、振型和阻尼比)的变化。因此，研究学者们以频率和振型为基础，提出更加敏感的损伤指标来检测结构的损伤。RAGHAVEN 等[5]基于模态柔度曲率的方法，对桥梁的损伤进行了识别；ZHAO J等[6]提出，相对于固有频率，模态柔度对结构损伤更加敏感；WU D等[7]有效证明了模态曲率可有效进行曲面损伤识别。HU Y等[8]利用模态应变能有效检测了复合材料表面损伤。YANG T等[9-10]利用模态柔度曲率矩阵和曲率模态差对复合材料进行了无损检测，通过实验和有限元模态分析方法对具有单损伤、多损伤和不同损伤程度的构件进行识别，验证了该方法的正确性。李永梅等[11]利用基于模态柔度矩阵的柔度曲率作为损伤参数的方法对桥梁损伤进行了准确的检测。颜王吉等[12]提出基于单元模态应变能灵敏度的方法，运用损伤的概率模型方法计算出各个单元损伤概率。郭利等[13]利用模态柔度曲率差的方法，对弯管结构进行了损伤识别，通过实验和仿真的方法，对不同位置和损伤程度的弯管结构进行了研究。

尽管基于结构振动模态的损伤检测方法在桥梁混凝土结构、金属结构中得到了广泛的应用。但由于复合材料的各向异性，将模态分析方法应用在复合材料结构损伤识别中的研究工作还很少。基于此，本文利用曲率模态变化率的方法对具有单损伤、多损伤和不同损伤程度的复合材料梁结构进行研究，探讨模态分析法在复合材料梁结构损伤识别中的适用性，为实现复合材料结构损伤的定位与定量识别，提供一种有效的无损方法。

1 曲率模态变化率

将复合材料悬臂梁看成一维无阻尼梁式结构，当自由振动时，运动微分方程为[14]

(1)

式中ν(x,t)为t时刻梁截面x处的横向振动位移；EI为梁截面抗弯刚度；m(x)为单位长度质量。

根据模态理论，系统的振动可由各阶模态的线性组合而成，式(1)的解可表示为模态的叠加形式，即

(2)

其中，j为模态阶数；φj(x)为j阶位移模态振型；qj(t)为模态坐标。根据弹性梁弯曲变形理论，任意截面梁弯曲振动曲线的曲率变化函数为

式中k(x,t)为曲率；ρ(x,t)为曲率半径；Cj(x)为j阶曲率模态。

由材料力学知，梁的弯曲静力关系为

(4)

式中M(x,t)为梁截面弯矩。

由式(3)和式(4)可知，曲率模态会随着梁结构的刚度变化而变化，曲率模态对结构损伤会有敏感性，且曲率模态和位移模态也是一一对应的关系。

由于现在缺乏能够直接测量结构曲率响应的传感器，因此利用中心差分法计算结构的CMS[15]：

(5)

式中j为模态阶数；i表示第i个测试点；l为相邻测试点之间的距离；Cj(i)为复合材料梁第j阶、i个节点的曲率模态。

通过CMS的一阶微分，可得到CMSI：

(6)

由式(5)和式(6)可知，当复合材料梁中存在损伤时，损伤位置对应的弯曲刚度就会降低。与此同时，CMS和CMSI就会在该点发生明显突变。因此，CMS和CMSI可以作为损伤识别的指标。

2 仿真算例

利用ANSYS对复合材料梁进行有限元模态分析，选用8节点实体单元SOLID46来模拟复合材料模型。建立长×宽×厚=300 mm×30 mm×4.08 mm的复合材料悬臂梁，每层厚度为0.17 mm，铺层方向为[0/90]6 s，其材料属性见表1。

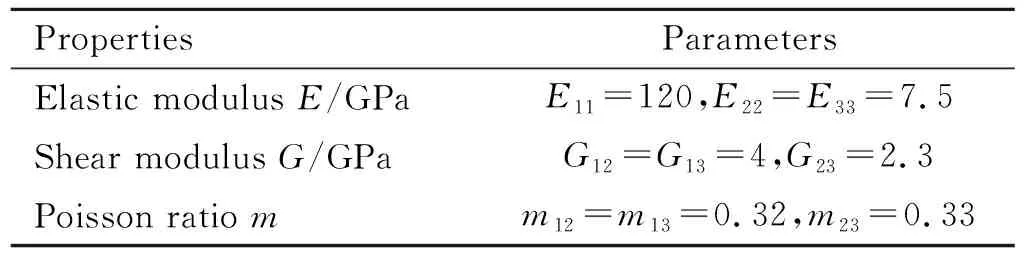
表1 碳纤维材料属性

将模型沿长度方向(X)划分为60个单元，共61个节点，离散后其计算模型如图1所示(图中上排数字为节点号,下排数字为单元号)。

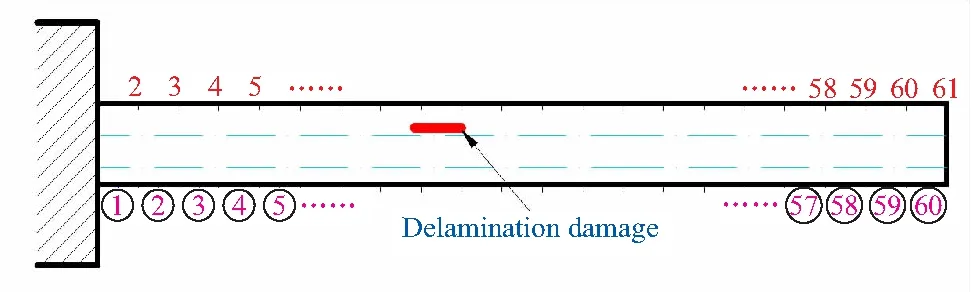
图1 复合材料梁计算模型

层间局部脱粘损伤是复合材料层合板最主要的损伤类型，采用节点共用法，脱层单元处层间不共用节点，其余各单元层间共用节点，来建立损伤区域的模型，进而来模拟损伤。有限元模型如图2所示。

(a) Unit division (b) Damage model

针对复合材料悬臂梁单损伤、多损伤和损伤程度的情况进行研究分析，总共分为5种工况，每种工况的损伤由位置、区域大小和数量来模拟。5种预设工况如表2所示。

表2 预设损伤工况

3 结果与讨论

3.1 模态参数识别

通过有限元模态分析，可得到复合材料梁仿真模型的固有频率和振型。由于实际工程中模态振型的高阶频率难以测量，仅提取了有限元复合材料梁的前三阶固有频率和振型进行分析。表2损伤工况中，Case1的有限元模拟的前三阶位移归一化振型如图3所示。可看出，未损伤单元和损伤单元的位移归一化振型没有显著差异，说明振型对损伤不敏感。为提高损伤识别的稳定性，将不同工况下的前三阶模态的分析结果代入到式(5)、式(6)中，计算各节点的CMS和CMSI的平均值，用于识别结构损伤。

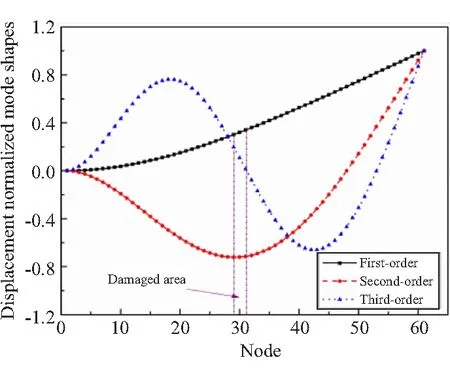
图3 前三阶位移归一化振型图

3.2 CMS损伤识别

从图4可看出，CMS在损伤位置发生突变，在未损伤的区域，CMS是光滑的。由此可得，CMS可识别复合材料梁的脱层损伤。

在图4(a)中，CMS在29～30单元处发生突变。但在图4(b)中，29～32单元出现显著突变。此外，其他未损伤单元的CMS是比较平滑的。突变的位置与表2中预设的损伤位置一致，表明CMS能够识别损伤并且能够确定损伤位置。尽管都是单损伤，Case 2的损伤面积却比Case 1大一倍，CMS可识别复合材料梁结构不同尺寸的损伤。

在图4(c)中，CMS在29～30单元和39～40单元发生突变，但39～40单元突变特征相对较弱，这与损伤位置(X方向)有关，且复合多损伤互相干扰，消弱了损伤识别的敏感性。突变位置与预设损伤位置一致，表明曲率模态CMS可对复合材料梁中的多损伤进行识别。

图4(d)和图4(e)分别对应表2中Case 4和Case 5。从图4中可看出，29～30单元处发生突变，表明试件在第29～30个单元发生损伤，这与预设损伤位置一致。同时，Case 4中，含有两个脱层损伤时，曲率模态突变极差值CMSD为79.84，而在含有三个脱层损伤的Case 5中，曲率模态突变极差值CMSD为141.47。对比图4(a)中的 Case 1，试件中只含有一个脱层损伤时，CMSD为45.04。结果表明，该方法可识别同一损伤位置处复合材料梁的损伤程度。

3.3 CMSI损伤识别

从图4可看出，CMS在损伤39～40单元发生突变，但突变不明显。因此，讨论曲率模态变化率CMSI这一损伤识别指标。图5为不同工况下复合材料悬臂梁的CMSI (Case 1～5)。CMSI的突变比CMS更明显。

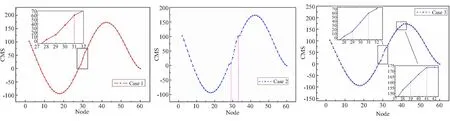
(a) Case 1 (b) Case 2 (c) Case 3

由图5中可看出，CMSI在损伤位置发生突变。图5(a)为单损伤和多损伤的复合材料的CMSI。Case 1的突变单位为29～30，Case 2的突变单位为29～32，而Case 3的突变单位为29～30和39～40，符合表2的预制脱层位置。而在Case 3中，突变单元为39～40时，CMSI的突变比CMS更明显。这说明CMSI可更加准确的识别复合材料中的单损伤、多损伤及不同程度损伤。图5(b)为不同损伤程度复合材料梁CMSI。CMSI突变大小与损伤程度有关。对于Case 1，Case 4， Case 5，随着损伤程度的增加，对应的曲率模态变化率的突变极差值CMSID分别为22.93，94.24，214.53。结果表明，CMSI值也可定量识别复合材料梁在同一位置的损伤程度。对于Case 3，在39～40单元的损伤情况下，对比图4中相应的CMS和图5(a)中CMSI，可清楚地看到，在相同的损伤情况下，CMSI的突变比CMS的突变更为显著。因此，可得出结论，CMSI比CMS对复合材料损伤识别更敏感。

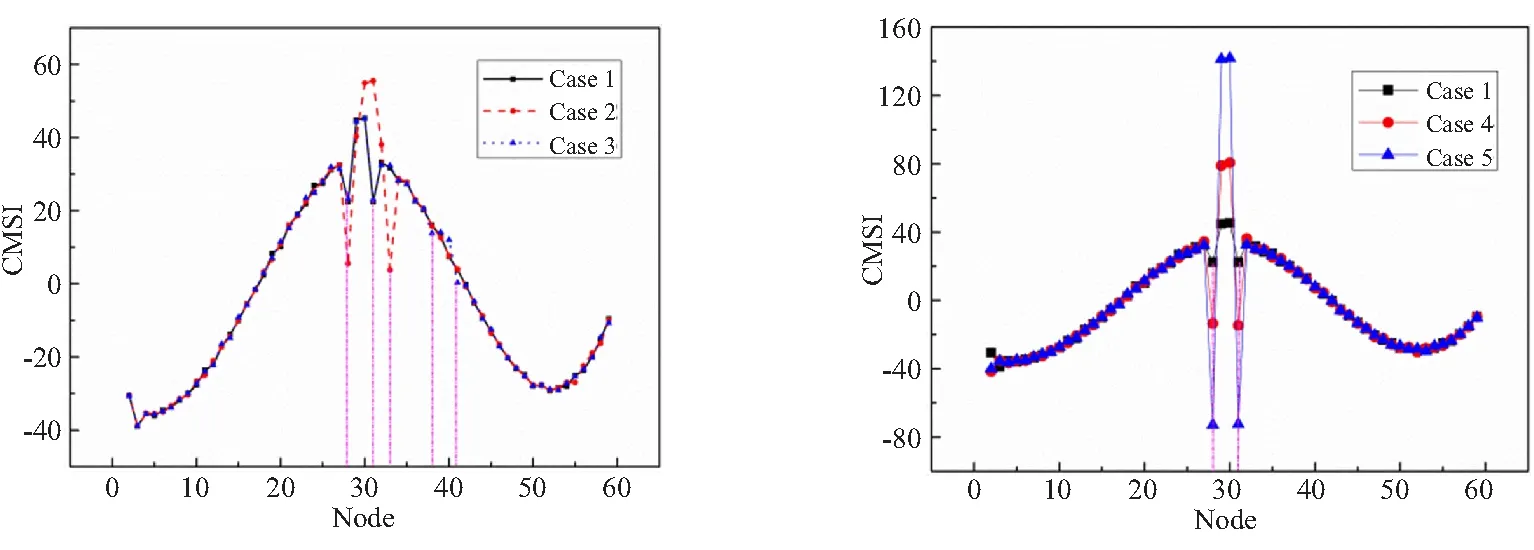
(a) Case 1, 2, 3 (b) Case 1, 4, 5

3.4 CMS 和CMSI与损伤程度关系

在损伤处的突变极差值CMSD和CMSID与损伤程度(脱层数)之间的关系如图6所示。从图6中可看出，CMSD和CMSID随着损伤程度的增加(脱层数量增加)而明显增加，表明采用CMS和CMSI可对复合材料梁的损伤程度进行定量识别。

图6 突变极差值与脱层数关系

4 结论

(1)应用有限元仿真软件ANSYS，对脱层损伤复合材料梁结构进行模态分析，得到各阶固有频率及节点振型，通过计算得到复合材料脱层梁的曲率模态和曲率模态变化率。

(2)以CMS和CMSI为损伤识别指标，对复合材料脱层梁进行损伤识别。结果表明，CMS和CMSI在损伤单元处都发生突变，可准确识别复合材料梁损伤的位置和大小。

(3)通过对不同损伤程度的复合材料梁的CMS和CMSI的CMSD和CMSID对比可得，两种损伤识别指标具有定量识别损伤程度的能力，且CMSI对复合材料梁结构损伤识别更为敏感。