双频投影条纹相位展开方法的改进

雷经发，陈志强，张 淼，孙 虹，李永玲

（1.安徽建筑大学 机械与电气工程学院，安徽 合肥230601；2.工程机械智能制造安徽省教育厅重点实验室，安徽 合肥230601；3.安徽省仿真设计与现代制造工程技术研究中心，安徽 黄山245041）

1 引 言

结构光三维测量具有非接触、全场性和高精度等优点［1-4］。其关键的核心问题之一是光栅相位场的解算，尤其是高效率和高可靠性的展开复杂形面的条纹图像相位主值［5-6］。目前，相位展开方法可分为空域法和时域法两大类。投影多频条纹根据外差原理进行相位展开的方法是时域相位展开法的典型代表之一［7］。此方法对被测目标表面的颜色不敏感，可以准确地展开复杂物体表面的相位主值，具有计算过程稳定、实用性强的优点，因而得到了广泛的应用［8-9］。

国内外很多学者对利用外差原理进行相位展开的方法进行了大量的研究。GUO等提出了投影双频条纹，分别建立高频或低频光栅相位与高度映射查找表的方法，实现了三维面形的快速高精度测量［10］。DONG等利用遗传算法补偿随机相位以增强外差信号的方法，在低信噪比环境下依然具有良好的解相效果［11］。WANG等采用先对条纹图像进行小面积自旋滤波处理再用外差解相的方法，进一步提升了算法的性能［12］。郭进等投影三种不同频率的条纹图像，使用三频外差原理展开相位主值的方法，很大程度上解决了周期次数非正常跳变的问题，降低了绝对相位的跳跃性误差［13］。陈松林等提出了一系列约束条件，进一步改进了三频外差相位展开法，解出的绝对相位光滑无跳跃［14］。随着研究的深入，涌现了很多有效的基于多频外差原理的相位展开方法，但这些方法都或多或少增加了辅助条件，复杂程度有所增大。

本文针对投影双频条纹在根据外差原理进行相位展开时绝对相位存在跳变性误差的问题，利用解相过程已有的必要结论和结果，先解出条纹级数小数部分的计算值和实际值，再结合相位主值自身的误差对相位展开算法进行了改进，以实现绝对相位校正。实验结果表明，改进的方法基本不增加额外的工作量，简单可靠，可以较好地校正绝对相位的跳跃性误差，具有实际应用价值。

2 外差解相原理

投影双频光栅条纹根据外差原理进行相位主值展开的方法的理论知识和公式推导过程参阅文献［15］和［16］。

若设不同频率光栅的条纹级数为ni，则可将条纹级数值分为整数部分N i与小数部分Δni相加，即有：

因此，若设各频率条纹的相位主值为φi，则条纹级数的小数部分与相位主值有如下关系：

本文统一将相位主值解到[0，2π]区间。若设各频率条纹的光栅节距为p i，则根据条纹叠栅特性可知叠栅后的条纹级数为同一级别，即其取值区间为[m，m+1]。则可分别求出两种频率投影光栅的条纹级数ni，n2如下式所示：

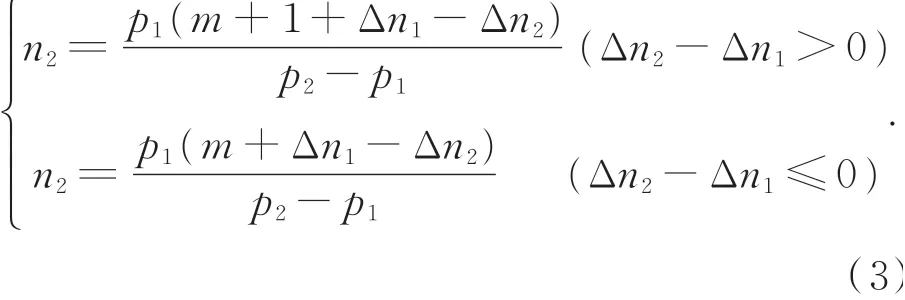
同理可解算另一个条纹级数。一般将解出的条纹级数进行向下取整得到其整数部分，并作为周期次数进行相位展开，得到：

式中θi为各频率条纹的绝对相位值。

3 改进方法的原理

3.1 投影图案的相位初值设定

在不考虑实时测量的情况下，应当优先使用相移法提取相位主值。四步相移法具有提取相位主值精度高、实用性强等优点［17-18］，因此本文采用四步相移法提取相位主值。

投影双频条纹图案中，某一频率下一组4幅相移图案可用公式表示如下：

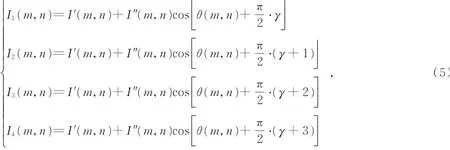
式中：γ∈Z，(m，n)表示图案中的像点坐标，I'(m，n)表示背景光强，I″(m，n)表示调制强度，θ(m，n)表示条纹图案的相位场。

当γ=0时，式（5）为通常的四步相移法，即投影的第一幅相移图案的相位初值为零，提取相位主值后，利用外差原理展开相位不仅会出现跳跃性误差，还会出现阶梯现象，如图1中蓝线所示（彩图见期刊电子版）；当γ=−2时，投影的第三幅相移图案的相位初值为零，提取相位主值后，利用外差原理展开的绝对相位仅出现了跳跃性误差，如图1中红线所示，这是改进方法需要解决的问题。因此，本文编制相移投影图案时取γ=−2，即投影的第三幅相移图案的相位初值为零。同时，利用四步相移法提取相位主值时要考虑反正切函数的象限问题，将相位主值的取值区间扩展到[0，2π]［19］。

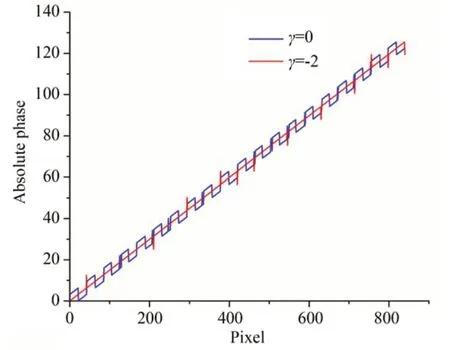
图1 相位初值对应的绝对相位Fig.1 Absolute phase corresponding to phase initial value

3.2 调整周期次数非正常跳变

根据式（3），不妨设：

实际上，Δn12为双频条纹叠栅后形成的虚拟光栅的条数级数的小数部分。令：

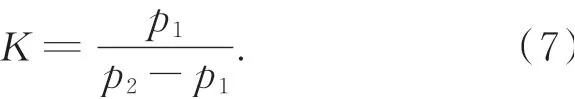
同时，假设叠栅后的虚拟光栅相位场的初始值为零，即m=0。联立式（6）和式（7），则式（3）可改写为：

式中K为常量。根据相位展开公式（4）可知，需对条纹级数进行向下取整操作，即：

式中符号［］表示向下取整运算。深入分析易知：理论上，当虚拟条纹级数的小数部分Δn12为1K的整数倍时，即Δn12=c K，c=1，2，3，4…，N2会发生正常跳变，即随着c变大，其逐步加1。但实际情况是，在理论值Δn12接近或等于c K时，由于误差等影响，实际的Δn12值可能会发生变化，导致条纹级数的整数部分，即周期次数发生不正常的跳变，如图2所示，最终的绝对相位也会出现跳跃性误差。

图2 周期非正常跳变示意图Fig.2 Schematic diagram of abnormal periodic jump

根据式（2）和式（4）可知，理想环境下，利用外差原理解出的条纹级数的小数部分的计算值Δn2c应与依据当前相位主值计算出的小数部分的实际值Δn2r相等。小数部分的计算值为：

而实际上由于相位主值自身误差等原因，两者并不相等。根据以上分析可知，若周期次数发生向上或向下跳变，小数部分的计算值与实际值之差的绝对值必定会大于某一值，且此值与相位主值自身误差紧密相关，可称为阈值T。

若已知各频率条纹的相位主值的自身误差，各频率条纹级数的小数部分可根据公式（2）算出，因此可将相位主值自身误差转化为小数部分误差。设Δn1的误差为δ1，Δn2的误差为δ2，则Δn12的 误 差 为(−δ1−δ2，δ1+δ2)，由 此 阈 值T为：

文献［20］指出，未校正过的四步相移法提取相位主值的误差不超过0.08 rad，且K值可根据光栅节距算出，则式（11）中所有量均为已知量。

综上，调整周期非正常跳变的方法可归纳如下：

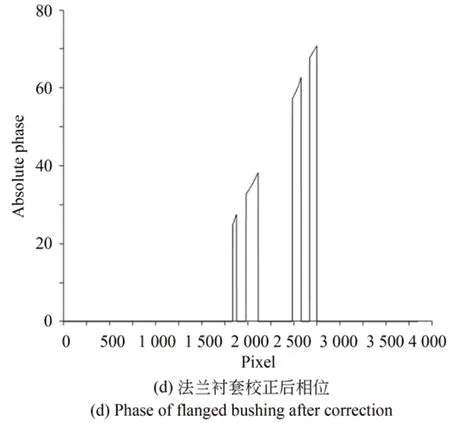
（1）若|Δn2r−Δn2c|

（2）若|Δn2r−Δn2c|≥T，且Δn2r−Δn2c>0，则周期次数出现向上跳跃，将此时周期次数值减一即可；

（3）若|Δn2r−Δn2c|≥T，且Δn2r−Δn2c≤0，则周期次数出现向下跳跃，将此时周期次数值加一即可。

根据上述分析可知，光栅节距较大的条纹的相位主值在利用外差原理直接展开时不容易出现跳跃性误差。

4 实验与结果分析

4.1 仿真实验

为验证改进方法的正确性与可靠性，仿真了光栅节距分别为40 pixel和42 pixel的两组四步相移条纹图案，其分辨率为720×840 pixel。根据四步相移法分别提取出两组各自的相位主值，如图3所示（彩图见期刊电子版）。

图3 双频条纹的相位主值Fig.3 Phase principal values of dual-frequency fringes

作为对比，在原始相移图中加入了不同的高斯噪声，再利用双频外差原理展开相位主值，并使用本文提出的改进方法校正绝对相位，判定阈值具体设为T=0.509，如图4所示。

图4 表示在不同均值和方差的高斯噪声条件下3组实验中绝对相位校正前后的分布情况。随后，统计各组绝对相位图中校正前后的跳跃性误差像素数，如表1所示。

图4 不同高斯噪声下的绝对相位Fig.4 Absolute phases with different Gaussian noises

表1 跳跃性误差点数Tab.1 Jumping error points

根据图4和表1可以看出，改进方法可极大程度地降低跳跃性误差点数，校正率可到90%以上，且加入噪声时也会改变相位主值的自身误差，但改进方法仍然表现出很好的校正结果，具有一定的抗噪性。

4.2 真实实验

为验证改进方法的实际应用价值，搭建了图5所示的测量系统。图像采集装置为康耐视工业相机，投影装置为腾聚DLP结构光发生器，两者光心相距约20 cm，投影装置光心距离物体约40 cm。

图5 双频投影条约相位展开改进方法测量系统Fig.5 Measurement system for improved unwapping method of dual-frequency projection fringe

控制投影装置投射与仿真实验中设定值一样的相移图案于被测物表面，并使用相机同步采集，利用四步相移法提取相位主值的双频投影光栅需采集8幅图像。以一个配油盘和一个法兰衬套作为被测物。其中，测量配油盘时所采集到的两种频率各自的第一幅相移图如图6所示。根据四步相移法提取出两种频率条纹各自的相位主值，如图7所示。

图6 不同频率的相移图Fig.6 Phase shift images at different frequencies

图7 不同频率的相位主值图Fig.7 Phase principal value images at different fre⁃quencies

利用外差原理展开相位主值，并用本文改进方法进行校正，阈值设定与仿真时一致，校正前后的绝对相位值如图8所示。图8（a）~和8（b）为配油盘校正前后的绝对相位值，取其相位图中横穿样件中心的第1 500行数据进行对比；图8（c）和8（d）为法兰衬套的法兰面校正前后的绝对相位值，取其相位图中横穿样件中心的第1 620行数据进行对比。

由图8可知，未校正前绝对相位存在跳跃性误差，而校正后展开的相位光滑无跳跃。使用标定好的测量系统，利用校正后的相位解出配油盘和法兰衬套的三维点云，分别如图9和图10所示。

图8 校正前后的绝对相位值Fig.8 Absolute phase values before and after correction

图9 配油盘元件的三维点云Fig.9 Three-dimensional pointcloud of oil distribution pan

图9 是利用配油盘表面的相位场和测量系统定标参量解出的三维点云数据，而图10是依据法兰衬套的法兰面的相位值解出的三维点云数据，点云模型特征与元件表面的绝对相位息息相关。被测物三维点云曲面或平面的平整性也可说明校正后的相位跳跃性误差得到了较好的抑制，改进方法有效可靠。

图10 法兰衬套的三维点云Fig.10 Three-dimensional point cloud of flanged bushing

5 结 论

本文针对投影双频条纹利用外差原理展开相位主值时会出现跳跃性误差的问题，基于解相过程，结合相位主值自身误差为条纹级数的小数部分的计算值和实际值之差设定一阈值，进而调整周期次数，消除非正常跳变。实验结果表明，在一定噪声和实际环境下，改进方法对绝对相位跳跃性误差的校正率可以达到90%以上，满足实际应用需求。

然而，投影双频光栅由于叠栅要求存在测量范围狭窄和投影条纹过粗等缺陷，后续会针对该问题展开进一步研究。