基于熵的过采样框架

张念蓬，吴 旭，朱 强

西安电子科技大学 数学与统计学院，西安710071

数据挖掘是一种在海量数据中寻找即时的、有价值的信息的技术[1]。经过近些年的发展，数据挖掘已经形成了很多行之有效的模型和算法，它们主要集中在分类、聚类、关联分析等方面。其中，分类也被称为有监督学习，这类算法需要对数据的特征和类标签进行分析处理，得到不同的特征组合与类标签之间存在的判别规律，并将这些规律以知识的形式保存下来。当需要为新的数据判定类别时，分类算法能利用之前学得的知识为其贴上预测标签。

尽管数据挖掘与机器学习技术日益趋向成熟并且被广泛应用于实际问题的处理中，但该领域仍面临着诸多挑战，如不平衡数据集分类问题。顾名思义，不平衡数据集中至少有一类数据的数量明显多于或少于其他类的数据数量[2]。这类问题应用十分广泛，如VIP 用户流失的检测[3]、欺诈交易识别[4]、医疗诊断[5]、银行破产预测和企业信用评估[6]等。

经典的机器学习算法和模型通常是基于“数据集是平衡的”这一假设建立的，若直接将它们应用在不平衡数据集上，性能会大幅下降。机器学习算法中的一个重要目标是最小化经验误差，即一个分类模型的目标是最小化总体分类误差，而少数类的分类结果对于总体来说影响是很小的。而且不平衡度越大，少数类对总体分类误差的影响越小。因此，分类器会通过主动保护多数类实例的方法来提升模型的整体性能，而忽视了对少数类实例的预测，甚至会将大量少数类实例误判为多数类。这样显然是不合理的。在不平衡数据的分类过程中，少数类数据的价值通常要大于多数类数据，而且随着不平衡度的增加，少数类数据的价值会越来越高。例如，在医疗诊断的过程中，将癌症患者误诊为健康的代价远高于将健康的人误诊为癌症患者的代价，该病人很可能会因此错过最佳的治疗时间，这带来的后果是非常可怕的。

1 不平衡数据的处理手段

用于提高不平衡数据集分类性能的技术整体上可以被分为两类：算法级方法和数据级方法。

算法级方法包括改进经典算法、代价敏感方法和分类器集成。修正分类算法以处理不平衡问题的策略是算法级技术[2]。代价敏感方法则是为不同的数据类型提供不同的错误分类代价。分类器集成是需要训练多个不同的弱分类模型，并按照特定的方式将弱分类模型组合起来，由它们的共同决策来预测数据的类标签，从而提高数据预测的准确性[7]。

数据级方法可以看作是一种独立于分类器的技术，用于重新平衡数据分布，使标准算法以用户的目标为中心[8]。特别地，数据级方法可以分为欠采样多数类实例[9]和过采样少数类实例[10]两种方案。欠采样方法通过减少多数类实例的数量来创建原始不平衡数据集的平衡子集。过采样方法通过增加少数类数据实例的个数来平衡数据集。Chawla 等人[11]提出一种基于线性插值的过采样算法SMOTE。SMOTE 算法的主要思想是随机选取一些少数类实例作为种子，并选取种子的k个最近邻中的一个或多个少数类实例，与其结合为邻居对适应合成过采样方法（ADASYN）[10]、边界SMOTE 算法（borderline）[12]、安全级SMOTE算法（safe）[13]等。

过采样技术通常是处理不平衡数据集的首选方法。传统的衡量类不平衡的指标是不平衡率IR，即多数类数据的数量与少数类数据的数量之比。IR反映了数据集在数量上的不平衡程度，但没有度量分布上的不平衡程度。即使数据集是数量平衡的，类分布的不平衡仍然可能存在[14]。此外，少数类集合的分类准确性与信息实例的数量有关，而与少数类实例的数量无关[15]。

因此，衡量少数类与多数类之间数据分布的不平衡程度是重要的。本文利用信息熵度量数据集的局部密度信息，从分布上考虑数据集的不平衡程度，并提出了基于熵的危险集的概念和它的三种使用策略，即基于熵的危险集过采样算法（EDgS）、基于熵的安全集过采样算法（ESS）和基于熵的自适应过采样算法（EAS）。基于熵的过采样框架具体分为三个部分：首先介绍了数据集熵差的具体计算方法和危险集的概念，这一部分是该框架的基础和起点；其次介绍了危险集的三种使用策略，分别是在危险集上过采样、在危险集的补集上过采样和自适应的过采样，这三种策略的侧重点不同，特点和优势也各不相同，适用于不同分布的数据集；最后，本文在算法中加入了生成实例的检测机制，若生成实例能通过检测，则该实例可以在数据分布的意义下平衡数据集，反之，该实例不具备平衡数据分布的能力，将其删掉即可。

2 信息熵的介绍

一个集合D的信息熵的计算公式如下：

其中，pi通常为第i条数据的概率，本文用基于距离的局部密度在整体密度中的权重代替。众所周知，熵可以度量数据分布的不确定性。因此，本文利用熵差来度量数据集分布的不平衡程度，这与以往的IR完全不同。

在图1 中，可以清楚地看到使用熵差（ED）的优点。这两个数据集具有不同的ED 和相同的IR。对于图1的A，两个类之间没有重叠区域，并具有清晰的分类边界，这使得任何一个简单的分类器都能很容易地完成识别；图1 的B 则完全不同。显然，IR 无法区分这两个分布不同的数据集。总之，这些少数类的代表性实例是研究少数类分布的关键。以往的研究表明，固定IR时，少数类中的代表性实例越多，分类器的分类性能越好[14-15]。因此，用IR作为测量不平衡度的唯一指标是不合适的。

图1 ED相同、IR不同的两个数据集

熵通常用来度量数据分布的不确定性，它可以看作是信息分布的反义词。换句话说，数据分布的随机性越强，它包含的信息就越少[16]。对于不平衡数据来说，更分散的类内分布和更少的数据量将意味着更高的熵。在这种情况下，熵被引入到输入空间中作为数据分布的度量方式。

另外，本文基于信息熵将少数类数据集分为危险集和安全集。如果一个少数类实例属于危险集，则表示这个实例周围的少数类分布比较稀疏，在这些区域过采样，可以有效扩大数据集中少数类的范围，反之则表示实例周围的少数类分布比较密集，在这些区域过采样，会降低错分多数类实例的风险。

3 基于熵的过采样框架

本章的主要内容是基于熵的过采样框架，具体可以分为以下三个部分：第一部分是数据集的熵的计算方法和计算过程中涉及到的统计量的含义，并在此基础上形成基于熵的危险集，讨论了危险集的意义；第二部分为危险集的使用策略和不同的使用策略所对应的含义，并给出不同策略对应的具体算法流程；第三部分通过实验验证了算法的有效性。

3.1 基于熵的危险集

本节介绍熵差的具体计算过程，并形成相应的算法流程。

给定一个训练数据集D，包含实例X={xi|x∈Rn,i=1,2,…,m}，实例所属类别为C={cl|l=1,2}，相应的实例数量表示为m1、m2。数据集D中的任意两个实例表示为xi=(xi1,xi2,…,xin) 和xj=(xj1,xj2,…,xjn)，这两个实例的距离计算公式通常定义为欧氏距离，如下：

使用公式（3）为给定数据集的第i个实例定义一个基于密度的实例位置统计量：

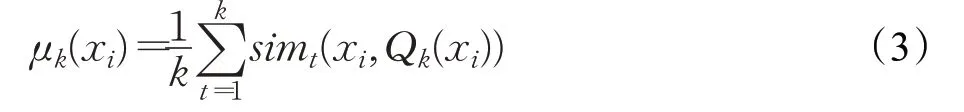
其中Qk(xi)表示xi的k近邻集合，sim(⋅,⋅)为相似度度量公式，通常使用欧氏距离。因此，μk(xi)是一个局部密度度量公式，用于测量xi距离其k近邻的平均距离，同时表达了实例xi附近的密度信息。第i个样本的基于密度的类位统计量由下式给出：

式中，ωi是xi在cl总密度度量中的比例。因此，每个实例的类内密度可以通过基于密度的类位统计来测量。xi附近的密度越高，μk(xi)和ωi就越小。换句话说，ωi的大小反映了xi的类内密度。

每一类的熵由公式（5）计算。令c1和c2分别代表少数类和多数类，容易得到E1≥E2>0。众所周知，熵是由信息量的多少和信息对称性决定的。实验结果表明，在不平衡数据集上，多数类和少数类的熵的大小通常依赖于信息量的多少。也就是说，少数类的类内熵通常大于多数类的类内熵。在此基础上，信息对称性影响类内熵的大小。为了度量数据集分布的不平衡程度，本文提出了一种新的度量方法：

另外，本文将少数类实例按ωi排序，截取较大的一半，用来形成危险集Dg。由此将少数类数据集分为危险集和安全集。如果一个少数类实例属于危险集，则表示这个实例周围的少数类分布比较稀疏，在这些区域过采样，可以有效扩大数据集中少数类的范围，但是也会提高错分多数类实例的风险；反之则表示这个实例周围的少数类分布比较密集，在这些区域过采样，虽然生成的实例的多样性有所下降，但同时也会降低错分多数类实例的风险。

数据集的基于熵的危险集算法（EDg）的具体细节见算法1。

3.2 危险集的使用策略

EDg 算法为每个少数类实例计算出基于密度的类位统计量，也就是数据分布意义下的权重，权重越大，说明该实例周围的类内分布越稀疏。因此，本节提出三种基于熵的过采样策略，分别是在危险集上过采样、在安全集上过采样和自适应的过采样策略。这三种过采样的策略在合成过程中都采用线性插值的办法，只是在选取种子对时有所不同。

基于熵的危险集过采样算法（EDgS）首先利用EDg算法求出危险集，其次在危险集上随机的选择种子对，并使用公式（7）实现线性插值：

其中δ∈U[0,1]，是均匀分布的随机数。最后检测整个数据集中ED的变化，若ΔED<0，则说明新实例在数据分布上平衡了数据集，是有价值的，应该保留；否则，删除新生成的实例。这样生成的新实例不仅可以在数据分布上平衡数据集，也可以有效扩大数据集中少数类的范围和多样性。EDgS的实现过程见算法2。

基于熵的安全集过采样算法（ESS）首先利用EDg算法求出危险集，在Cmin上求Dg的补集，得到安全集Ds，其次在Ds上随机的选择种子对，并使用公式（7）实现线性插值；其余的步骤与EDgS 算法相同。但相较于EDgS 算法，ESS 算法生成的新实例的多样性会有所下降，错分多数类实例的风险也会显著降低。ESS的实现过程见算法3。

基于熵的自适应过采样算法（EAS）首先为每个少数类实例赋权，权重为ωi；然后在考虑权重的基础上随机选择少数类实例xp，在Q(xp)中随机选择xq，并使用公式（7）实现线性插值；其余的步骤与EDgS算法相同。

与EDgS 算法和ESS 算法相比，EAS 算法可以有效增加生成的少数类数据的多样性，减小错分多数类实例的风险。EAS的实现过程见算法4。

本节利用危险集的思想，给出了一个基于熵的过采样策略的框架，并在此框架下得到EDgS、ESS和EAS算法，这3 个算法在理论上各有侧重。如EDgS 在危险集上生成新实例，会显著增加少数类数据的多样性；ESS在安全集上生成新实例，更加注重生成实例的安全性；EAS则在整个少数类数据集上自适应的生成少数类，是前两种算法折中的结果。

3.3 实验结果及分析

为验证提出的算法的有效性，本节选取来自UCI[17]和KEEL-dataset repository[18]中的6 个二分类数据集进行实验仿真，它们的详细介绍见表1。每个数据集分别通过7 种过采样算法（SMOTE、borderline、EDgS、safe、ESS、ADASYN、EAS）进行处理，且选择SVM 作为基分类器。评价指标选择AUC和召回率，因为AUC能客观地反映分类器对不平衡数据集的综合预测能力，召回率能反映出分类器对少数类实例的分类准确度。显然，AUC和召回率的值越大，算法的性能就越好。

表1 二分类数据集的描述信息

表2 和表3 分别列出了8 个算法在6 个数据集上的AUC和召回率的得分和排名的详细信息。

表2 8个算法在6个数据集上的AUC得分和排名

表3 8个算法在6个数据集上的召回率得分和排名

对于基于线性插值的算法来说，borderline 和EDgS都是在危险集上进行过采样，safe和ESS都是在安全集上进行过采样，ADASYN 和EAS 都是在整个少数类数据集上进行自适应的过采样。因此，将上述算法两两之间进行对比是比较合理的。可以看出，提出的EDgS、ESS和EAS的AUC得分均强于borderline、safe 和ADASYN。特别是EAS 算法，在对ADASYN 算法进行提升的同时，也在多个数据集上取得了很好的名次，如数据集abalone17vs78910、alocks0 和ecoli0vs1。这体现了本文提出的算法在综合预测能力上的优势。

不平衡数据分类问题中少数类实例通常更加珍贵，因此少数类被正确分类的比例是很重要的。本文算法在召回率得分上显示出非常强的竞争力。用于实验的6个数据集中，基于熵差的过采样算法只在ecoli0vs1上表现一般，这可能是由于该数据集的ED很小，而IR较大，相较于传统的不平衡度量方法，本文算法不能很好地识别少数类和多数类。

4 总结与展望

本文利用熵信息来度量数据集的不平衡程度，为各种变量赋予实际意义，并给出用熵差计算数据分布不平衡度的具体方法；另外，利用熵信息计算出每个点周围的局部密度，得到了基于熵的危险集。随后给出了危险集的使用策略和对应的算法，即EDgS、ESS 和EAS 算法。实验证明，本文的研究内容可以有效提升经典过采样算法的性能。但不可否认的是，该理论和模型也存在一定的局限性，即对熵差较小的数据集的识别能力较差。针对这个问题，可以将IR和ED相结合，在利用ED检测数据分布的不平衡度的同时，使用IR 来体现数据集数量上的不平衡度，从而进一步提高对数据集的综合识别能力。这也是接下来的研究内容和方向。