靶板强度对射孔弹穿深影响的有限元仿真

徐 浩，李明飞，窦益华

（西安石油大学机械工程学院，西安 710065）

0 引言

随着完钻井深的不断增加，储层岩石压实度、强度和地层压力也不断增大，普通射孔弹无法达到射孔穿深要求，因此需采用超强射孔弹射穿污染带。另外，现有方法通常对低强度混凝土靶进行模拟，深井下储层岩石强度常超过70 MPa，因此需开展射孔弹侵彻高强靶有限元分析。

现有文献针对射孔弹侵彻高强靶数值分析较少。文献[1]研究了不同装药结构对混凝土穿深的影响，包括药型罩锥角、药型罩材料、药型罩壁厚、药型罩的曲率半径、聚能装药外壳以及炸高；文献[2]应用LS－DYNA软件对某型石油射孔弹装药结构下聚能射流形成、侵彻钢靶过程进行了数值模拟及分析，并与实验数据作了对比；文献[3]研究了射孔弹侵彻砂岩靶实验，分析了药型罩材料、壁厚、开口角度等因素对穿深的影响。文献[1－3]为射孔弹侵彻试验研究。分析可得，实验成本较高，模拟井下实际工况，建立射孔弹—射孔枪—射孔液—套管—超强砂岩靶模型试验几乎没有。文献[4]结合室内材料试验及有限元分析法，分析了不同深度的直井和水平井中套管承受非均匀载荷的力学性能；文献[5]应用ANSYS/Workbench模块，建立射孔段管柱三维有限元模型，在井下实测冲击载荷作用下，分析了管柱的动力响应规律；文献[6]应用ANSYS/Workbench建立了某规格射孔弹侵彻圆柱体应力砂岩的有限元模型，分析了侧向与轴向应力值分别为0、50 MPa时射孔弹侵彻砂岩的深度。文献[4－6]均为通过力学模型对射孔过程进行分析，但理论分析假设过多，没有考虑枪、套管、射孔液的影响，结果难免存在偏差。文献[7]采用LS－DYNA软件，模拟了矩形射孔弹射流的形成过程及其钢靶侵彻过程；文献[8]采用LS－DYNA软件，模拟了射流成型及其对混凝土靶板的侵彻过程，研究了不同锥角对聚能射流成型和侵彻的影响；文献[9－11]用LS－DYNA软件，模拟了射流侵彻过程；文献[12]用AUTODYN软件，仿真分析了聚能射流形成、侵彻钢板过程；文献[13]应用LS－DYNA软件对聚能装药在不同起爆方式下的射流形成过程进行了三维数值模拟；文献[14]用AUTODYN对油田使用的射孔弹的爆轰压垮药型罩过程和射流侵彻套管过程进行了模拟计算。文献[7－14]为射孔侵彻的数值仿真研究。分析可得，数值模拟大多只是对射流成型过程进行模拟，并未涉及射流侵彻过程，并未建立完整射孔弹—射孔枪—射孔液—套管—超强靶模型模拟出实际穿深。文献[15－17]主要研究了ALE算法在相关领域的应用，给出了相关的研究方法和技巧，为本文的研究提供借鉴和参考。

综上所述，射孔侵彻往往针对普通射孔弹侵彻低强度靶板进行仿真分析，且考虑计算机时问题并未计算至射流终止。本文应用LS－DYNA软件，结合ALE算法，以某油田深井下射孔为例，建立HS35－5型射孔弹侵彻不同强度混凝土靶三维模型。通过建立非反射边界条件，消除爆轰波对射流成型和效果的干扰；通过调整关键部位网格密度、优化不同接触面间的网格协调，减少数值畸变，提高分析精度，降低机时。本文研究可为实际井下射孔弹侵彻高强靶的仿真分析提供方法参考。

1 有限元模型建立

1.1 几何模型

为了研究不同强度混凝土靶HS35－5射孔弹射流射流速度变化及穿深，建立1/4射孔弹—射孔枪—射孔液—套管—混凝土靶模型。模型参数：井深5 500 m、射孔段深度5 000 m，地层压力梯度1.0，射孔处地层围压50 MPa。HS35－5射孔弹参数为：弹高54 mm，射孔弹直径46 mm，炸药类型为RDX，装药质量35 g，药型罩高度40 mm，药型罩外径36 mm，压入深度2 mm，罩重100 g；炸高15 mm；套管外径178 mm，壁厚12 mm；射孔枪外径102 mm，壁厚6 mm；混凝土靶厚度设置1 200 mm。单枚1/4射孔弹—射孔枪—射孔液—套管—混凝土靶几何模型如图1所示。

图1 1/4 HS35－5射孔弹侵彻混凝土靶三维模型

1.2 三维有限元模型建立及网格划分

射孔弹—射孔枪—射孔液—套管—混凝土靶模型选择3D164单元；图2所示为整个模型有限元网格划分示意图，其中射孔弹头部包括炸药、药型罩网格加密；射孔枪、套管、混凝土靶板采用渐变式网格划分方法，即与射流接触侵彻部分加密其网格数量，其余部位减少网格数量。其中空气单元数为65 630、壳体4 500、炸药3 500、药型罩2 352、枪管1 000、套管1 080、射孔液800、混凝土靶24 000。

图2 1/4HS46射孔弹侵彻混凝土靶三维模型网格

1.3 材料模型选择

1.3.1 炸药材料

HS35－5射孔弹采用RDX装药，选用的材料模型是HIGH＿EXPLOSIVE＿BURN材料模型，炸药爆炸产生的冲击波压力采用JWL方程，其表达式为：

式中：P为等熵压力；V＝ρ0/ρ＝v/v0为相对比容；A、B、R1、R2、ω为待定常数；E为单位体积的内能。

炸药密度为1.8 g/cm3，分析参数如表1所示。表中，MID为材料编号：RO为密度；D为爆速；PCJ为Chapman－Jouget压力；BETA为燃烧标志；K为体积模量；G为剪切模量；SIGY为屈服应力；EOSID为状态方程ID；A、B、R1、R2、O MEG、E0为炸药状态方程参数，这里为定值；V0为初始相对体积。

表1 炸药分析参数（HIGH＿EXPLOSIVE＿BURN）

1.3.2 药型罩材料

药型罩的材料为紫铜，固态金属药型罩转化成液态高速金属流体过程中涉及大范围固液转化，选用MAT＿STEEINBERG材料模型。该材料模型在模拟材料变形、状态转化等方面较为准确。该模型的特性为屈服强度随温度和压强的变化而变化，在该模型中，剪切模量G和屈服强度σs均随压力增大而增大，但随温度升高而降低。当材料达到自身熔点时，G和σs都接近0。

材料熔化前的剪切模量G为：

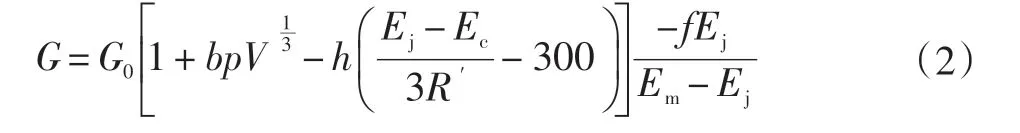
屈服强度σs为：

式中：p为压力；V为相对体积；Ec为冷压缩能；Em为融化能；R′＝Rρ/A，R为气体常数，A为原子量。若Em＞Ej，则有rj为初始塑性应变，当时，令。当材料融化后，σs和G设置为初始值的一半。

药形罩本构方程采用EOS＿GRUNEISEN，药型罩材料具体分析参数如表2所示，状态方程分析参数如表3所示。

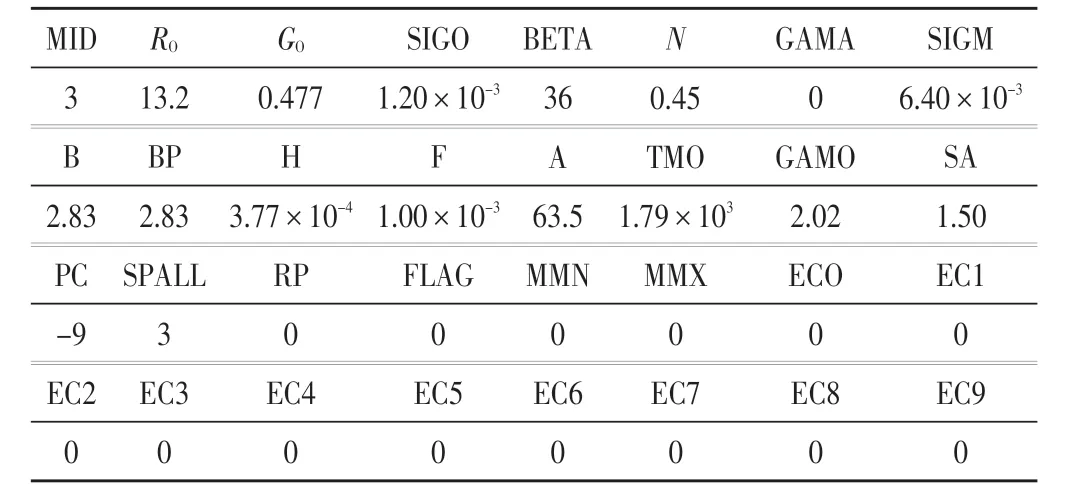
表2 药型罩材料模型分析参数（MAT＿STEEINBERG）

1.3.3 混凝土材料

混凝土强度为80 MPa，用于模拟深井下岩石储层，采用JOHNSON＿HOLMQUIST＿CONCRETE模型，分析参数如表3所示。表中，MID为材料编号；RO为密度；G为剪切模量；A为规范内聚强度；B为归一化压力；C为应变速率系数；N为压力硬化指数；FC为准静态单轴抗压强度；T为最大拉伸静水压力；EPSO为参考应变率；EFmin为断裂前塑性应变；SFMAX为标准化的最大力量；PC为沉重压力；UC为破碎体积应变；PL为锁定应力；UL为锁定体积应变；D1、D2为损害常数；K1、K2、K3为压力常数；FS为故障类型。

表3 混凝土材料模型分析参数（JOHNSON＿HOLMQUIST＿CONCRETE）

1.3.4 有限元算法设置

有限元模型中，空气、炸药、药型罩、射孔液等在形成超高速金属射流和射流侵彻射孔枪、射孔液、套管及混凝土靶的过程中，具有大变形和高速流动的特点，运用欧拉算法进行冲击动力学仿真，对模型的网格精度要求较高，导致计算机时较长，数值分析成本较高；拉格朗日算法虽然对模型网格要求不高，但模拟固液转化过程质量不高；ALE算法也叫任意欧拉拉格朗日法，其中包含欧拉算法以及拉格朗日算法，对有限元模型中的空气、炸药、药型罩、射孔液采用欧拉算法，细化网格；射孔枪、套管、弹壳、混凝土靶有限元模型采用La⁃grange算法，相比于欧拉算法，可以减小网格数量，降低机时。实际射孔中，射孔枪与套管、混凝土靶互相之间并不会有所接触，但在LS－DYNA中，在金属射流侵彻的过程中，射孔枪与套管、混凝土靶之间通过射流头部会有接触的可能，若不设置接触类型，易导致计算出错。因此拉格朗日算法单元射孔枪与套管、射孔枪与混凝土、套管与混凝土靶之间均需要设置接触类型，接触类型采用ESTS侵蚀接触。

2 有限元动态仿真过程

图3给出了金属射流形成及侵彻过程，炸药产生的巨大冲击波在轴线方向叠加给金属药型罩施加高温高压，药型罩微元从轴向顶点到侧向底边依次发生变形，在轴线方向上发生激烈碰撞，在尾端形成直径较大的杵体、前端形成细束金属射流，射流依次穿过射孔枪，侵彻套管、射孔液、混凝土靶板。图3（a）所示为药型罩发生变形形成射流的过程，此时射流沿轴向方向被压垮，开始形成射流；图3（b）～（d）分别为金属射流侵彻枪管、射孔液、套管及混凝土靶状态。

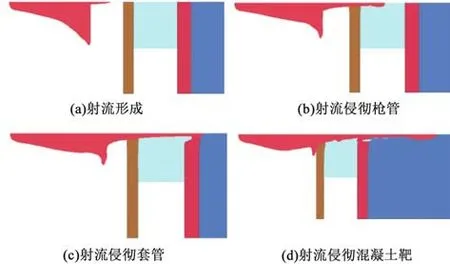
图3 射孔弹侵彻动态过程

3 不同强度靶板射孔弹侵彻速度分析

3.1 轴向速度

图4所示为不同靶板强度射流侵彻混凝土靶轴向速度曲线。射流侵彻70 MPa、90 MPa及110 MPa混凝土靶轴向速度曲线趋势大致相同，27μs时，射流穿过套管开始侵彻混凝土靶，此时射流头部轴向速度为5 027 m/s，射流在250μs之前速度下降较快，250μs之后速度下降较缓。射流侵彻70 MPa混凝土靶轴向截止速度为600 m/s；射流侵彻90 MPa混凝土靶轴向截止速度为700 m/s；射流侵彻110 MPa混凝土靶轴向截止速度为802 m/s。射流侵彻90 MPa混凝土靶轴向截止速度较70 MPa混凝土靶提高14.3%；射流侵彻110 MPa混凝土靶轴向截止速度较70 MPa混凝土提高33.7%。结果表明，由于靶板强度的提高，相同射流截止轴向速度提高，从而导致射流侵彻能力降低。

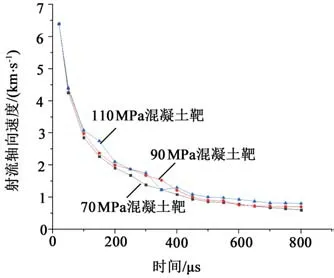
图4 不同强度混凝土靶射流轴向速度变化曲线

3.2 径向速度

图5 所示为射流侵彻不同强度混凝土靶径向速度曲线。由图可知，射流侵彻70 MPa、90 MPa及110 MPa混凝土靶轴向速度曲线趋势大致相同，在侵彻靶板之前，射流径向速度均为704 m/s，射流径向速度在250μs之前下降较快，250μs之后下降较缓。与轴向速度不同，射流径向速度并不是一味下降，而是会出现波动，初步分析为射流在侵彻过程中出现多次断裂，射流会断裂成好几段碎片，只剩头部继续侵彻，当射流中部断裂时，射流碎片将不会继续向前侵彻，射流碎片所携带能量会使射流持续扩孔，从而导致射流径向速度波动。从3种工况下分析射流径向速度可以发现，射流侵彻110 MPa混凝土靶径向截止速度最大，其次为90 MPa混凝土靶，最后为70 MPa混凝土靶。由此可知，靶板强度的增大将会提高射流径向截止速度，这与射流轴向截止速度分析大致相同。

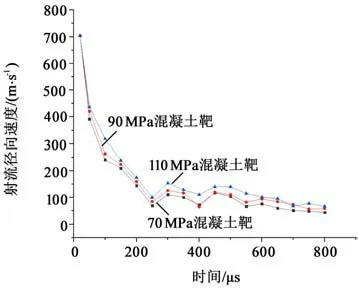
图5 不同强度混凝土靶射流径向速度变化曲线

4 不同强度靶板射孔弹侵彻深度分析

图6所示为3种工况下选取不同时间点位移，利用Origin软件所绘制的位移时间曲线。从图中可以看出，3种工况下射流穿深曲线趋势大致相同，射流侵彻70 MPa混凝土靶穿深约为670 mm；射流侵彻90 MPa混凝土靶穿深约为640 mm，对比70 MPa混凝土靶穿深下降4.5%；射流侵彻110 MPa混凝土靶穿深约为603 mm，对比70 MPa混凝土靶穿深下降10%。在750μs后，3种工况下射流穿深曲线逐渐平缓，无明显变化。在开始阶段，侵彻速度较快，尤其是在500μs之前，而在600μs后，射流侵彻速度明显减慢。随着靶板强度的增加，射孔弹侵彻深度逐渐降低。

图6 不同强度混凝土靶射孔弹穿深变化曲线

5 结束语

本文应用LS－DYNA软件，模拟超深井下工况，建立1/4完整射孔侵彻的三维有限元模型，并在砂岩外围施加50 MPa围压，应用ALE算法，给定炸药参数，模拟爆轰过程，真正实现了爆轰过程、药型罩固流转化、射流高速侵彻套管的大变形和流固耦合仿真，无围压下射流穿深与试验穿深误差为1.5%，得到如下结论。

（1）通过优化不同接触面间的网格协调，减少数值畸变，提高分析精度；通过建立1/4射孔弹模型、调整关键部位网格密度，减少网格数量，降低机时。

（2）70 MPa混凝土靶射流轴向临界速度为600 m/s，径向临界速度为44.2 m/s；90 MPa混凝土靶射流轴向临界速度为700 m/s，径向临界速度为58.8 m/s；110 MPa混凝土靶射流轴向临界速度为802 m/s，径向临界速度为67.2 m/s。随着靶板强度的增加，射孔临界速度提高。

（3）70 MPa混凝土靶射孔弹侵彻深度为670 mm；90 MPa混凝土靶射孔弹侵彻深度为640 mm；110 MPa混凝土靶射孔弹侵彻深度为603 mm。随着靶板强度的增加，射孔弹侵彻深度逐渐降低。