复合材料机翼结构多约束优化设计

卢 杰，聂小华，常 亮

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

复合材料因其重量轻、强度高、设计性能好、易于整体成型、耐化学腐蚀、耐疲劳等优点而广泛用于各个领域，特别是在航空航天工业中，设计目标是“力争减轻每克的重量”[1]。通过提高结构效率和减轻结构重量，复合材料能够达到增加结构耐久性并降低成本的效果。复合材料的各向异性力学性能使其在设计过程中需要比金属结构考虑更多复杂的要素。然而，目前对复合结构的研究还不如金属结构成熟，这使得复合结构的设计更加困难。

本次优化主要以某型飞机机翼结构的梁缘条尺寸，腹板、翼肋腹板厚度为优化对象，并使优化结果在结构重量减轻的情况下满足结构应变约束、位移约束和稳定性约束等要求[2]。具体的工作如下：确定梁的截面形式及截面尺寸，如C字梁、矩形梁等的缘条尺寸和腹板尺寸。确定翼肋的几何尺寸及厚度，确定蒙皮的形式及厚度，形式统一采用蜂窝夹层蒙皮，确定内外蒙皮壁板的厚度及蜂窝夹芯的厚度，利用PMI泡沫夹芯对梁腹板进行增稳。

本文结合某型飞机机翼结构设计需求，以结构重量为优化目标，将单元应变、结构位移、结构扭转角以及结构稳定性等约束考虑在内，通过Nastran优化设计功能，对结构的尺寸进行优化设计。

2 优化方法

满应力设计是处理应力约束的一种简单而有效的优化准则，其特点是收敛快，不受设计变量数目限制，能给出满足结构静强度约束条件(应力、应变)的结构总体尺寸分布[3]，广泛用于飞机结构初步设计和详细打样设计中。

采用改进的满应力设计方法，其强度比再设计的一般步骤分为4步[4]。

(1)求各部位关键元的最大强度比

(1)

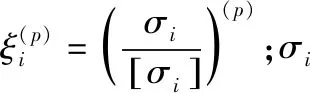
(2)强度比再设计

(2)

式中，Ai为可调尺寸；k为迭代次数；β为松弛系数。

(3)射线调参

W′=ξmax·W

(3)

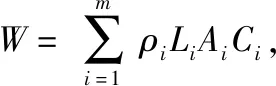
(4)收敛判断

(4)

式中，|ΔW|为重量变化率；ε为控制收敛的小数。

结构采用满应力设计减重效果较明显，但满应力设计方法只能满足应力条件，扭角约束和位移约束这两个设计指标需要通过广义位移设计来控制，最终结构才能满足设计要求。广义位移约束设计属数学规划法设计范畴，通常这类优化设计归结为求解下述数学规划问题。

寻找一组设计变量xi，i=1,2,…,q，即x={x1,x2,…,xq}，使得目标函数W(x)达到最小，并满足以下约束条件：

gj(x)≤0，j=1,2,…,N

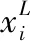
3 机翼模型的尺寸优化

本文的优化模型指的是包含目标函数、约束函数、设计变量以及优化方法等信息在内的有限元模型。在结构优化设计领域，通常都以结构重量最轻为优化目标。软件MSC.Nastran的结构优化模块也将目标函数默认为结构重量。基于Nastran的优化设计功能对设计得到的优化模型进行分析迭代计算，更新设计变量以实现结构轻量化设计。

3.1 有限元模型说明

该机翼结构蒙皮采用T300材料，面板的铺层定义为[0/±45/90]s，每个角度初始厚度为0.1mm，利用蜂窝夹芯对蒙皮进行增稳，蜂窝夹芯厚度5mm。梁腹板采用T300平纹碳布，面板的铺层定义为[0/±45/90]s，每个角度厚度为0.2mm，利用PMI泡沫夹芯对梁腹板进行增稳，PMI厚度60mm。翼肋采用T300材料，面板的铺层定义为[0/±45/90]s，每个角度厚度为0.4mm，利用PMI泡沫夹芯对翼肋腹板进行增稳，PMI厚度10mm。梁缘条采用T800材料，梁缘条截面是矩形，其宽度W和梁腹板PMI厚度一致，初始尺寸W=60，H=30。副翼蒙皮、梁腹板、翼肋和梁缘条均与机翼相同。

机翼结构有限元模型如图1所示，模型共有3513个节点，5170个单元，采用梁单元模拟缘条，用壳单元模拟蒙皮、肋、前后梁等结构。展向布置37个肋，机翼根部节点固支，机翼气动载荷按照力和力矩等效的方式施加到有限元节点上，具体采用多点载荷等效方法。结构包括3个舵面，作用于舵面的载荷通过刚体元施加。

图1 机翼结构有限元模型

3.2 设计变量说明

设计变量是指优化模型中影响目标函数的变量，通常包括几何参数和物理参数。机翼结构有限元模型的设计部位包括机翼的上/下蒙皮、翼肋、前/后梁缘条和前/后梁腹板。其中，蒙皮、梁腹板和翼肋结构将复合材料各铺层厚度作为设计变量[5]，复合材料铺层形式如图2所示。梁缘条将其宽度和厚度作为设计变量，各个部位细化分区，机翼蒙皮进行了37个设计分区，机翼梁腹板进行48个分区，机翼梁缘条进行96个设计分区，翼肋进行37个分区。

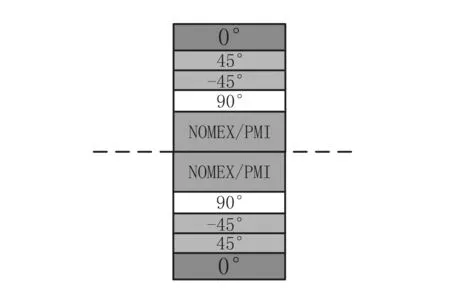
图2 梁/肋/蒙皮复合材料铺层结构

3.3 约束条件说明

在优化设计中，目标函数取决于设计变量，设计变量的范围具有各种限制，例如强度、刚度等。每个约束可以写为包含设计变量的函数，称为约束条件或设计约束，因其是设计变量的函数，也称为约束函数。飞机结构设计中常见的约束有几何约束、应力约束、位移约束及可靠性约束等[6]。对本例的约束条件分析如下。

应变约束：结构中的复合材料的单元应变应满足轴向压缩应变不大于4000με，轴向拉伸应变不大于5000με，面内剪切应变不大于7600με。

位移约束：通过位移约束控制结构变形，翼尖挠度不大于2000mm。

扭角约束：通过控制节点组合变形以控制最大扭转角度不大于1.5°。选取翼梢肋与前后缘相接的一对节点，通过控制该对节点法向位移实现对扭角的控制。

稳定性约束：蒙皮部位稳定性的安全裕度大于1.2。

3.4 优化控制参数设置

参数定义包括：循环次数设置，满应力优化次数上限设置，设计变量增量控制，输出数据控制，收敛判断条件控制等。

4 优化结果分析

4.1 优化初始模型分析

在对结构进行优化设计前，首先要对初始结构进行静力分析，统计结构重量、结构最大变形、单元最大拉伸应变、压缩应变和剪切应变等结果，用作与优化后的结果对比。

初始模型重量为712.3kg，经过对初始模型的静力分析，得到结构最大变形为1050mm，最大变形发生在翼梢处，变形云图见图3。

图3 机翼优化前结构位移云图

4.2 优化后的尺寸、位移与稳定性结果

使用Nastran的优化流程对优化模型求解计算，经过7次满应力优化和13次规划法优化迭代，结构重量的变化率满足收敛要求[7]。优化后蒙皮、梁、肋的铺层厚度与缘条的尺寸均发生了变化，优化后的蒙皮具体尺寸见图4。

图4 优化后机翼的蒙皮厚度分布

将优化后的尺寸回代入有限元模型中，模型的属性得到更新。对新模型进行静力分析，得到的位移分布情况如图5所示。从位移云图可以看出，优化后的结构最大变形为1650mm，发生在翼梢处。最大变形小于约束值，控制点处的扭角为1.48°，同样小于约束值。图6为优化后机翼的应变云图，可以看到，结构应变均未超过许用值，稳定性分析结果如图7所示，稳定性安全裕度满足设计要求。

图5 机翼优化后结构位移云图

图6 优化后机翼的应变云图

图7 优化后稳定性分析结果

经过优化设计，优化目标及约束均已得到满足。各结构的厚度尺寸进行了更新，通过静力分析和稳定性分析，新模型的计算结果满足工程实际要求。输出优化过程中的重量迭代结果，绘制曲线如图8所示，可以看出，经过优化设计，结构的重量变为287.1kg。

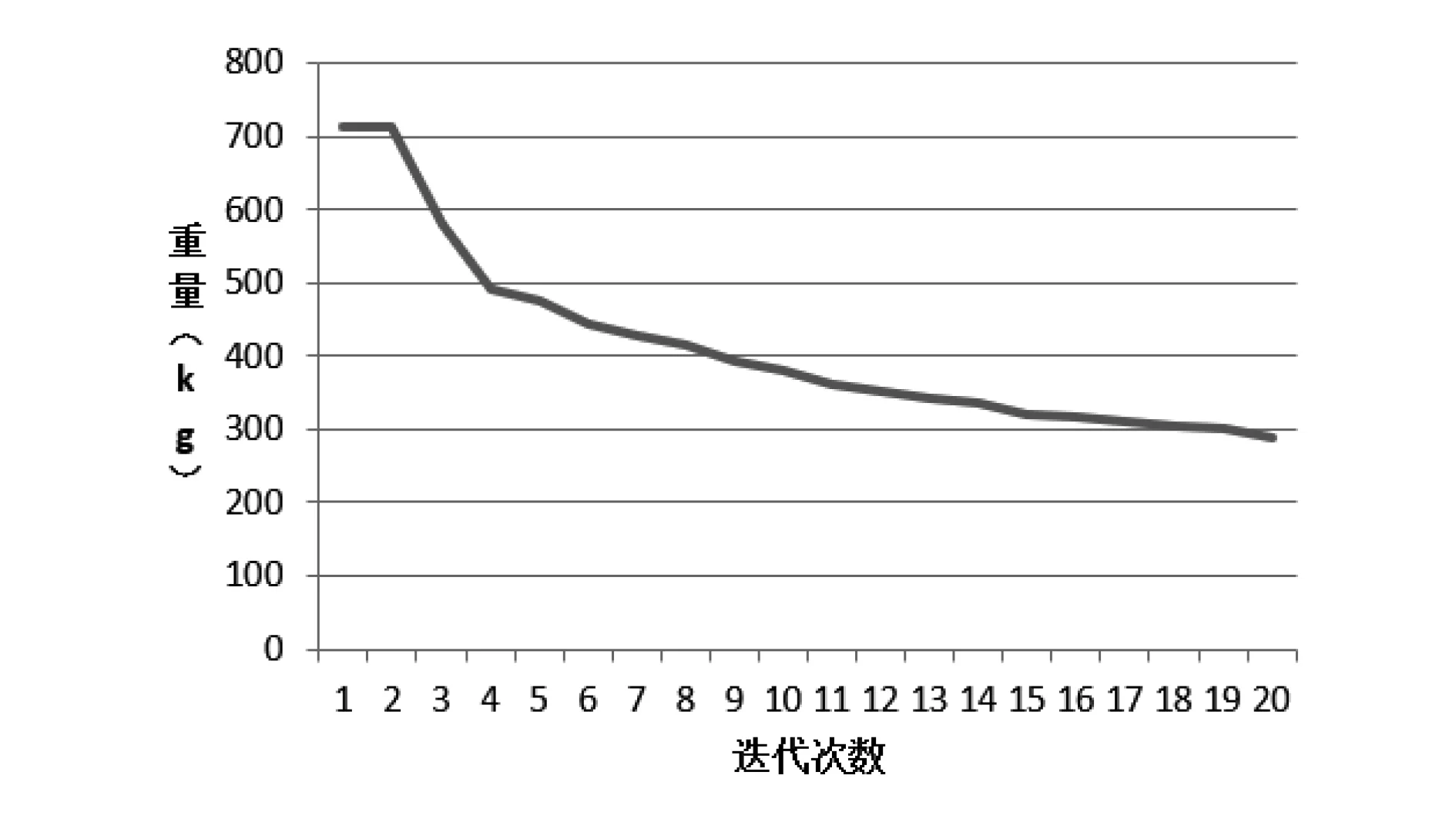
图8 重量迭代过程

5 结 论

通过对机翼模型进行细节优化，得到了优化后的结构尺寸及铺层厚度，在满足位移、应变、应力、扭角和稳定性的设计要求下，结构重量降低了59.7%。针对目前复合材料广泛应用于飞机结构的背景，该分析与优化方法对复合材料飞机结构的减重设计有重要的意义。