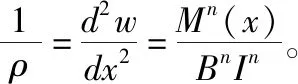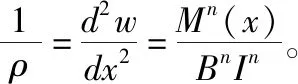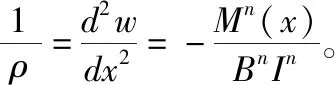物理非线性材料梁的弯曲变形解析解

吴 晓，罗佑新，李叶林

(湖南文理学院 机械工程学院，湖南 常德 415000)

1 引 言

伴随着物理非线性材料结构在工程实际中的推广应用，文献[1]研究了非线性材料静不定杆系的内力求解；文献[2]研究了非线性材料静不定梁的弯曲变形，但没有指出非线性材料静不定梁内力有可能是复数；文献[3]研究了非线性材料RC双曲冷却塔在风作用下的破坏过程；文献[4]采用直接强度法研究了非线性金属结构材料轴压短柱承载力；文献[5]采用一种新评价方法研究了材料非线性结构的抗震性能；文献[6]研究了钢筋混凝土薄板的热屈曲。文献[1-6]的研究工作说明，物理非线性材料结构已引起科研人员的较多关注。文献[7]研究了静定物理非线性材料结构的变形，文献[8]研究了非线性材料杆件的位移计算，文献[9]研究了物理非线性材料梁的弯曲变形。文献[7-9]的研究说明，物理非线性材料结构计算已引入高等院校材料力学实验教学中。文献[10]研究了静不定物理非线性材料梁的内力计算，但给出了错误结果。基于上述因素，本文给出了物理非线性材料梁的弯曲变形解析解。

2 弯曲变形微分方程

由材料力学可知，梁内距中性层为y处的应变是：

(1)

式中，ρ为曲率半径，y为任意点至中性层的距离。

假设应力与应变的关系为：

(2)

式中，B、n为材料系数。

由于梁弯曲时，梁横截面上的弯矩应为：

(3)

把式(1)、式(2)代入式(3)中可得：

(4)

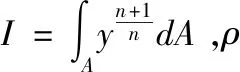
由式(4)可知，物理非线性材料梁的弯曲变形微分方程为：

(5)

假设以梁挠度向上为正方向，以梁中性轴向右为正方向。当梁截面弯矩为正时，其弯曲曲率也为正，因此无论n为奇数还是偶数，物理非线性材料梁的弯曲变形微分方程皆为式(5)。梁截面弯矩为负时，其弯曲曲率也为负，当n为奇数时，物理非线性材料梁的弯曲变形微分方程也为式(5)。梁截面弯矩为负时，其弯曲曲率也为负，当n为偶数时，要使物理非线性材料梁的弯曲变形解析解不出现复数，其弯曲变形微分方程应为：

(6)

由式(6)可知，梁截面弯矩为负、弯曲曲率也为负，当n为偶数时物理非线性材料梁的弯曲变形微分方程才能左右同号，物理非线性材料梁的弯曲变形解析解才可以为实数解，否则出现复数解，与材料力学不相符。

3 物理非线性材料梁弯曲变形

下面以n=2时物理非线性材料梁为例，研究梁的弯曲变形。

以图1所示梁为例，可知梁截面弯矩方程为：

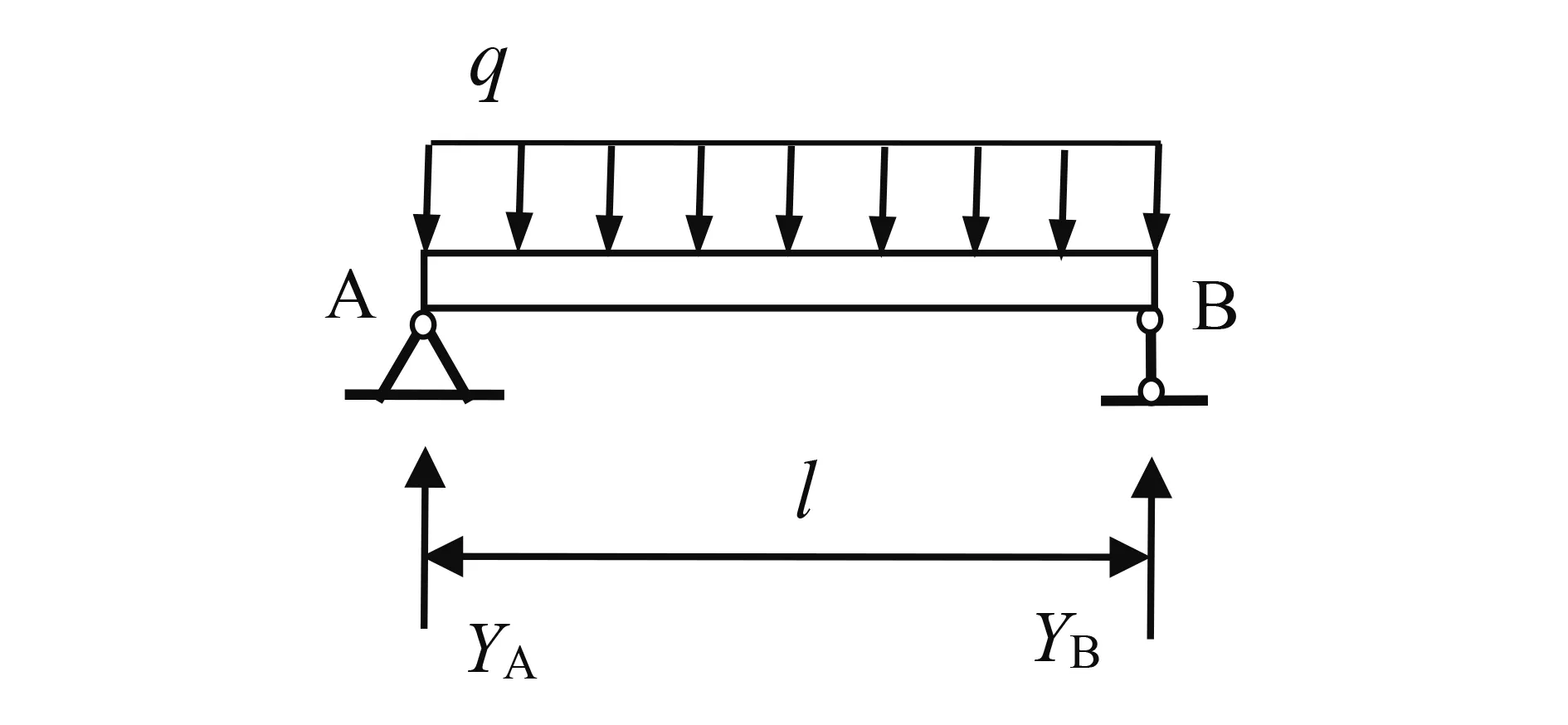
图1 均布载荷作用下简支梁

(7)

由于图1所示梁截面弯矩皆为正，把式(7)代入式(5)中可得：

(8)

把式(8)对x连续积两次分可得：

(9)

式中，A1、B1为积分常数。

图1所示简支梁的边界条件为：

x=0,w(0)=0；x=l,w(l)=0

(10)

由式(9)、式(10)可知，图1所示简支梁挠曲线方程为：

(11)

下面求图2所示一次静不定物理非线性材料梁的支撑反力。梁截面弯矩为：

图2 一次静不定梁

(12)

由于图2所示一次静不定物理非线性材料梁，在0≤x≤a时截面弯矩为正，在a≤x≤l时截面弯矩为负，因此令式(12)等于0，可求得：

(13)

当0≤x≤a时，把式(12)代入式(5)中积分可得梁段转角方程、挠度方程分别为：

(14)

(15)

当a≤x≤l时，把式(12)代入式(6)中积分可得梁段转角方程、挠度方程分别为：

(16)

(17)

图2所示一次静不定物理非线性材料梁的边界条件为：

(18)

图2所示一次静不定物理非线性材料梁的0≤x≤a梁段与a≤x≤l梁段的连接条件为：

(19)

利用式(13)-式(19)可得方程：

a6-7.5a2l4+12al5-5l6=0

(20)

利用式(20)可求得：

a1=0.7692l,a2=-1.9648l

(21)

式(21)中，显然a2=-1.9648l不合理，应舍去。把a1=0.7692l代入式(13)中并利用静力平衡方程可求得：

YA=0.3846ql,YB=0.6154ql,MB=0.1154ql2

(22)

如果图2所示一次静不定物理非线性材料梁，在0≤x≤a时截面弯矩为正、a≤x≤l时截面弯矩为负，把(12)代入式(5)中积分可得式(14)、式(15)，再利用边界条件式(18)可得方程：

(23)

由式(23)可以求得：

(24)

式中，i2=-1，i为虚数单位。

再利用静力平衡方程可求得：

(25)

由式(24)、式(25)可知，图2所示一次静不定物理非线性材料梁的支撑反力皆为复数，这与实际情况是不相符的。而文献[10]采用广义变分原理给出图2所示一次静不定物理非线性材料梁的支撑反力为：

(26)

本文作者采用单位载荷法、文献[10]的广义变分原理都只能得到方程式(23)，而由方程式(23)只能求得式(24)、式(25)。那么，文献[10]是如何求得式(26)的呢？本文作者经过反复演算发现，文献[10]作者是采用叠加法得到式(26)的。众所周知，求解非线性梁内力及挠度是不能采用叠加法的，文献[9]等其他文献也都明确指出了这一点。所以，文献[10]作者采用叠加法得到图2所示一次静不定物理非线性材料梁的支撑反力为式(26)是错误的。本文的研究结果对实际工程设计及材料力学教学都有理论指导意义。

4 结 论

在假设以梁挠度向上为正方向，以梁中性轴向右为正方向的前提下，可得以下结论：