一类波动方程解的生命跨度的估计
明 森,钟文倩,范雄梅,苏业芹
(1.中北大学 理学院,太原 030051;2.西南财经大学 证券与期货学院,成都 611130)
考虑如下初边值问题
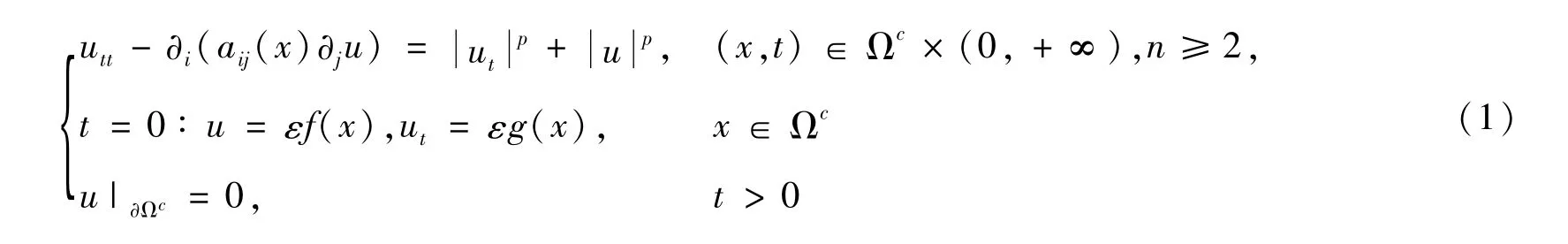
其中Ωc=Rn\B1(0),Ω=B1(0)为Rn中的单位球;ε>0是一个小参数。f(x)与g(x)∈(Ωc),并且
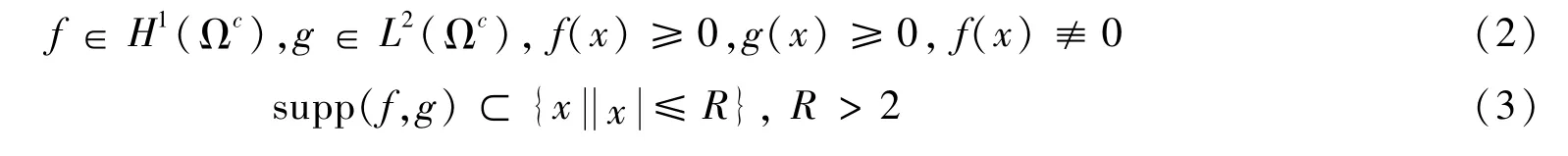
A(x)=表示光滑的n×n实对称矩阵函数。存在常数C>0,使得≤aij(x)ξiξj≤,∀ξ∈Ωc,x∈Ωc。aij(x)=≥R。重复指标i,j表示求和。若aij=δij,则问题(1)为常系数问题,其中δij为Kroneckerδ函数。
近来,关于如下非线性波动方程的Cauchy问题
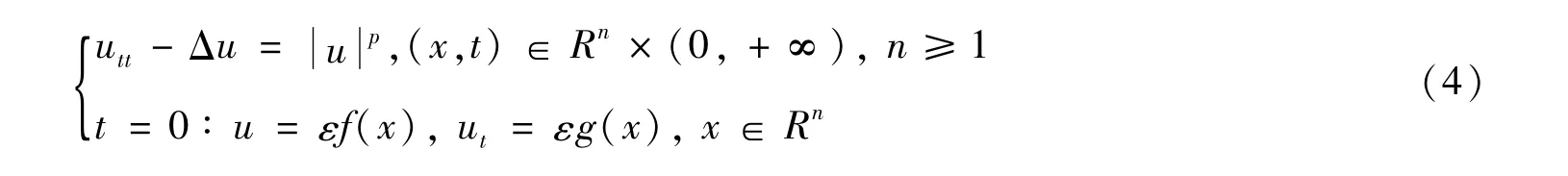
解的破裂与生命跨度的估计被广泛关注。1979年,John[1]在三维且p>p1(3)时证明了问题(4)存在整体解,而当1<p<p1(3)= 1+时,解在有限时刻破裂。Strauss[2]给出猜想:当p>p1(n)时,问题(4)存在整体解;当1<p<p1(n)且在有限时刻时解会破裂,此处p1(n)=为r(n,p)=-[(n-1)p2-(n+1)p-2]=0的正根。当n=1时,p1(1)=+∞。当n=2时,Glassey[3]证明了1<p<p1(n)时解将破裂。当n=4且p>p1(4)时,Zhou[4]得到问题(4)具有整体解(详见文献[5-9])。Zhou等[10]在1<p≤p1(n)(n≥3)时证明了初边值问题的解将出现破裂。对于Cauchy问题
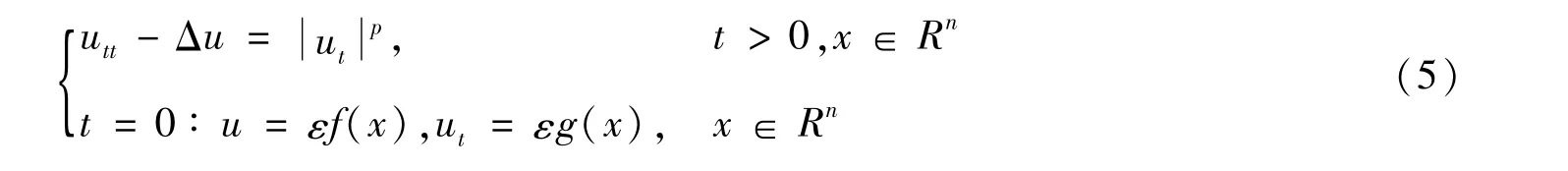
Glassey[11]给出猜想:当p>p2(n)=1+2/(n-1)时,问题(5)存在整体解;当1<p≤p2(n)时,解会在有限时间内破裂。当n=1时,p2(1)=+∞。文献[10]在1<p≤p2(n)(n≥1)时,证明了解会破裂(详见文献[12-16])。Han等[14]在全空间中得到常系数与组合非线性项情形的波动方程解的破裂性态。
问题(1)解的破裂结果见如下定理1和定理2。
定理1 设1<p≤p2(n)=,问题(1)的解满足
则解u的生命跨度T(ε)的估计为
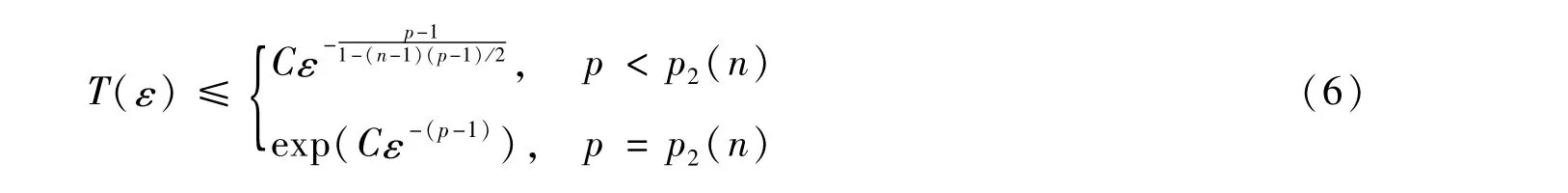
其中C为不依赖于ε的正常数。
定理2设,问题(1)的解满足
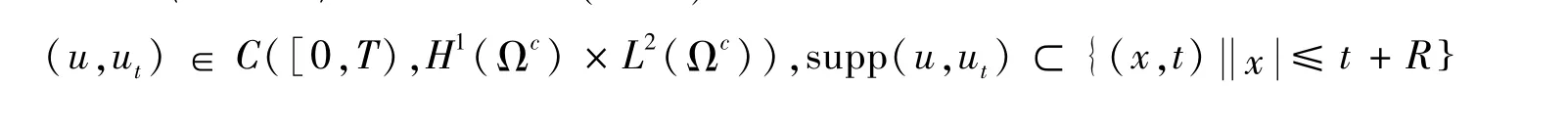
则问题(1)的解u会在有限时间内破裂,且式(6)可替代为
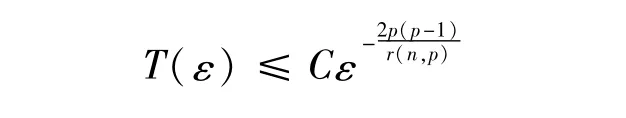
注结合定理1与定理2中的T(ε)的估计,可知

从而说明定理2中非线性项指数p的范围优于定理1中p的范围,且定理2中解的生命跨度的上界估计更佳。另外,本文利用检验函数方法与Kato引理将文献[14]中的小初值问题的部分结论推广至外区域上且带变系数的初边值问题。
1 定理1的证明
首先,给出Kato引理等相关引理及证明过程。
引理1[14]设a≥1,β>1,(β-1)a>α-2。若F∈C2([0,T))且满足
(a)F(t)≥δ(t+R)a
其中k、δ、R为正常数,则F(t)会在有限时间内破裂,且F(t)的上界估计T(δ)满足
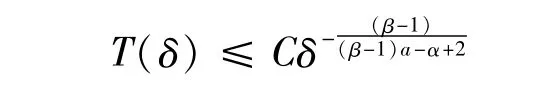
其中C是依赖于k,R,但不依赖于δ的正常数。
对于问题(1),首先考虑如下两类问题

其中f(x),g(x)满足式(2)和(3)。
引入检验函数ϕ0,ϕ1∈C2(Ωc),详见文献[10]中定理2.2和定理2.3。记

引理2[10]假设(f,g)满足式(2)和(3),且问题(7)的解满足
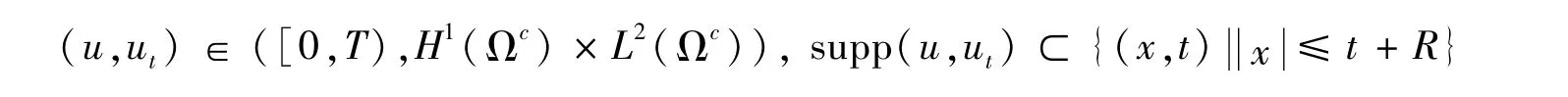
则对∀t≥0,有

式中c0为正常数。
引理3设问题(7)具有与引理2相同的假设条件。则当1<p<p1(n)时,问题(7)的解将会破裂,并且生命跨度满足

证明:由文献[10]中引理2.2可得

在问题(7)两边同乘以ϕ0(x)并在Ωc上积分,结合式(10)得到

利用Hölder不等式及式(11),可得
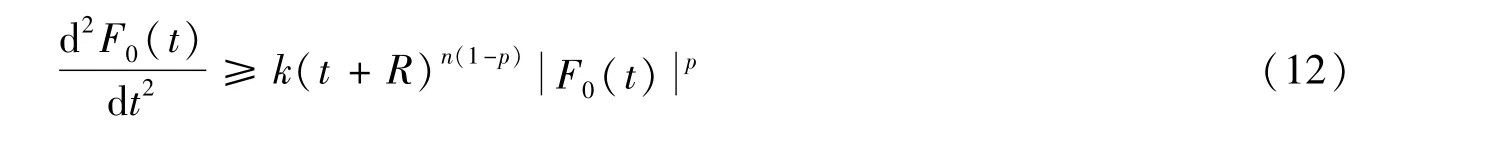
其中k=[Vol(Bn)]1-p>0。另一方面,有

利用式(11),引理2和文献[10]引理2.5得到
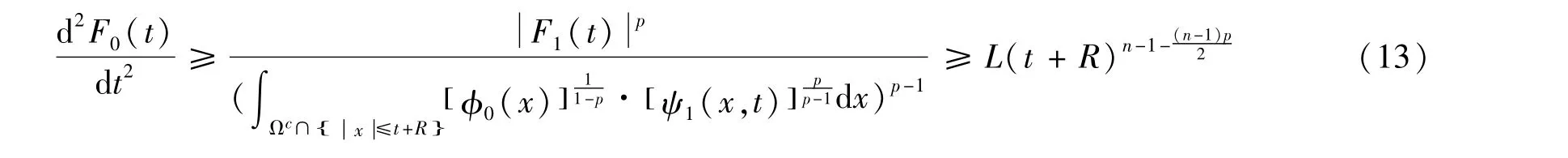
其中L=。对式(13)在[0,t]上积分2次,当t充分大时则有

其中
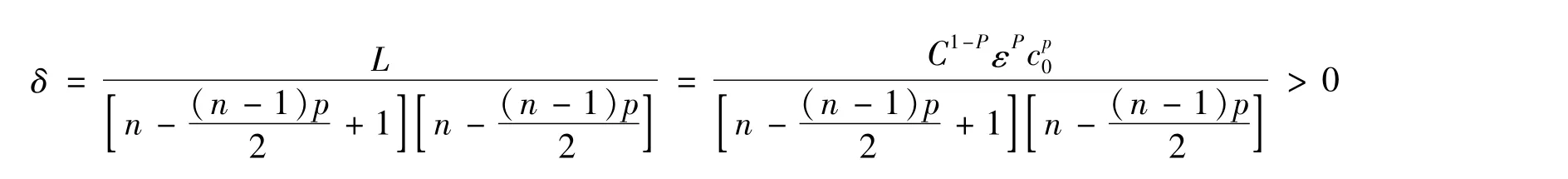
结合式(12)和(14),取参数a≡n+1-≡n(p-1),β≡p,当1<p<p1(n)=时,结合引理1可导出式(9),证毕。
引理4设问题(8)具有与引理2相同的假设条件。当1<p≤p2(n)时,对于问题(8),解的生命跨度估计为
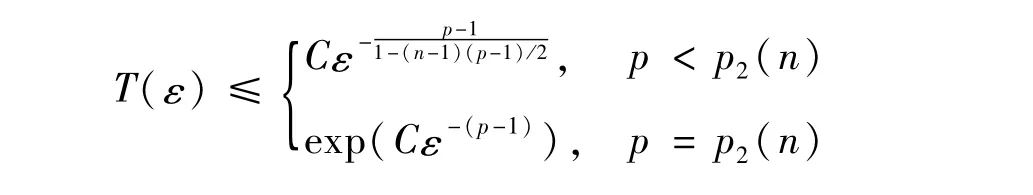
证明:利用ψ1(x,t)=e-tϕ1(x)及文献[10]引理2.3可知
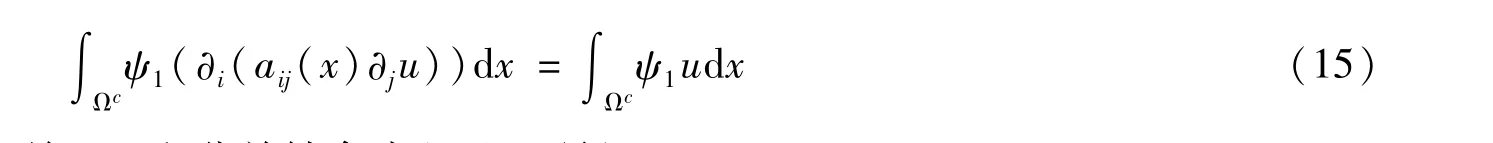
在问题(8)两边同乘以ψ1,关于x积分并结合式(15),可得


记

利用式(2)(16)和文献[10]引理2.3得


记
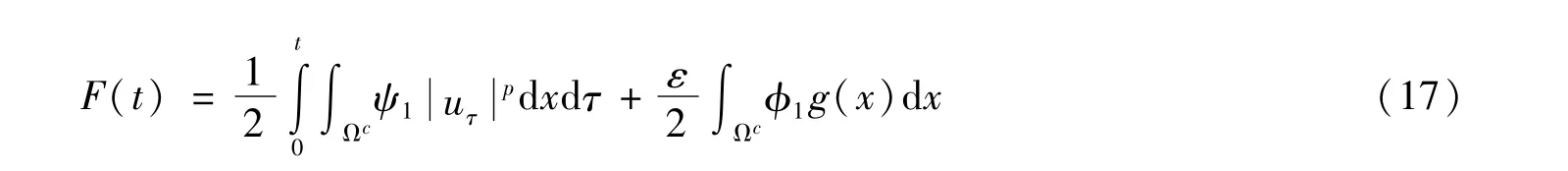
由于F(t)≥0,∀t≥0,利用文献[10]中引理2.6得
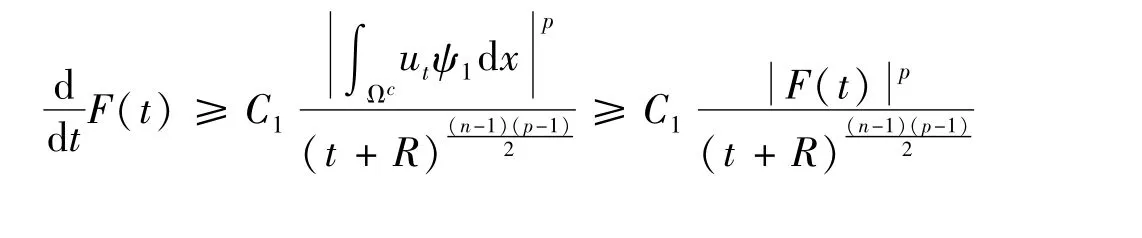
即
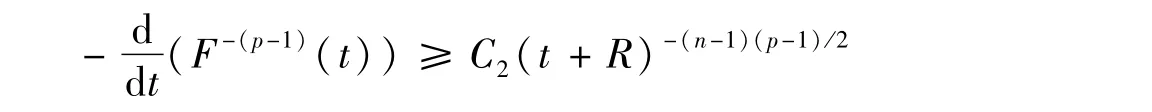
当p<p2(n)时,通过求解Riccati方程并利用式(17)可得
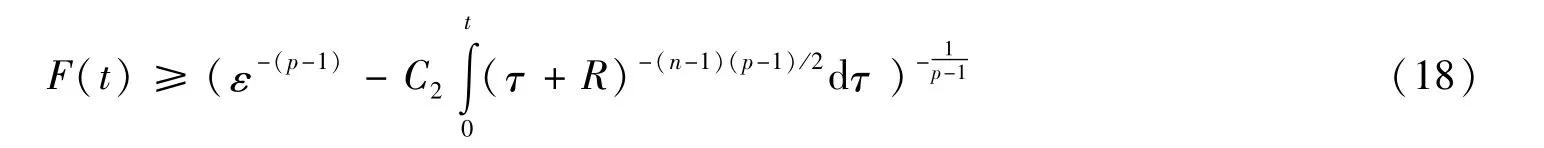
即T(ε)。
当p=p2(n)时,则有T(ε)≤exp(Cε-(p-1))。从而得到引理4中的结论,证毕。
运用式(7)(8)及叠加原理,从而得到定理1中式(6),证毕。
2 定理2的证明
在问题(1)两边同乘以ψ1(x,t),并对x积分,结合式(15)得到
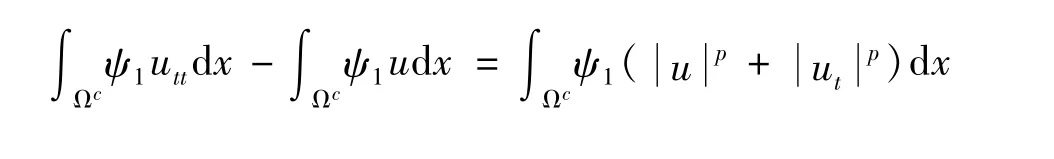
从而

类似地,计算得到

因此,记

由于


因此,由式(19)~(21)得

记I(t)=。利用问题(1),可得

因此,I(t)满足
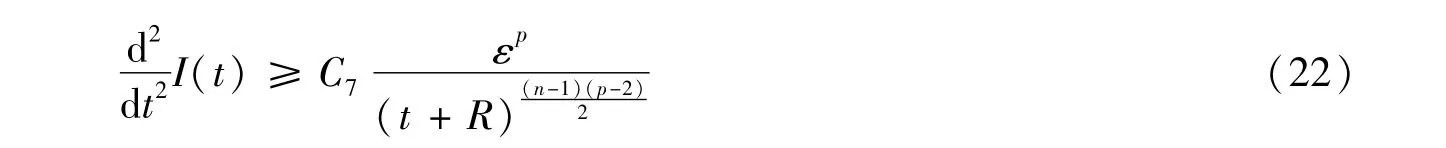
利用Hölder不等式可得
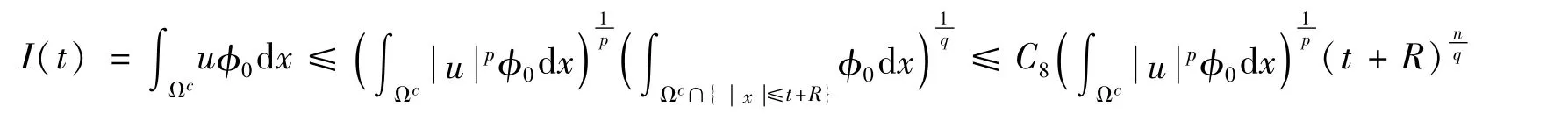
从而得到
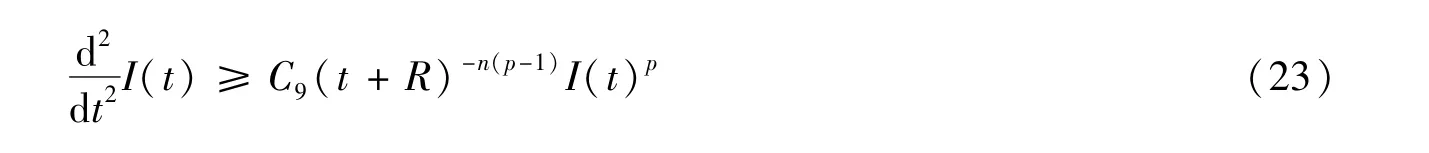
对式(22)关于t积分2次,当t充分大时,可得

利用式(23)与(24),取a≡2-,α≡n(p-1),β≡p,利用引理1,选取δ=εp即得定理2中T(ε)的估计,证毕。

